Acoustics and Vibration Animations
Daniel A. Russell
Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons License CC BY NC ND This work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License . Based on a work at http://www.acs.psu.edu/drussell/demos.html . Additional information about using this content is available at http://www.acs.psu.edu/drussell/Demos/copyright.html .


The content of this page was originally posted on January 16, 2024
HTML code was updated for accessibility and HTML5 compliance on July 10, 2025 .

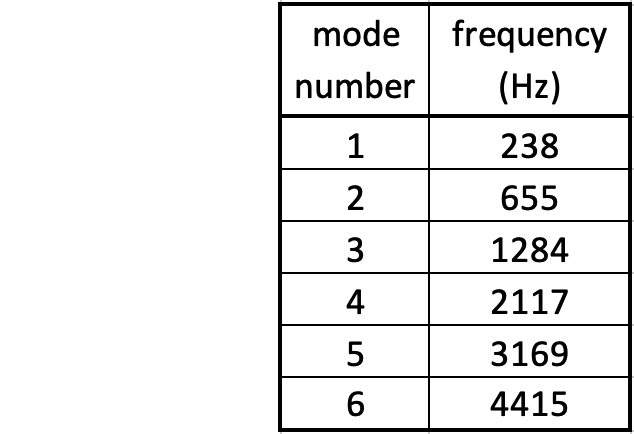
Flexural Bending Modes for a Thin Rectangular Bar

The animations on this page make use of the cividis colormap, which is supposed to be one of the best colormaps to enable someone with color blindness to visualize scientific data.
  • Jamie R. Nuñez, Christopher R. Anderton, and Ryan S. Renslow, "Optimizing colormaps with consideration for color vision deficiency to enable accurate interpretation of scientific data", PLOS ONE, (August 1, 2018), https://doi.org/10.1371/journal.pone.0199239
Here is a link to a red-blue color version of the same animations.

The animations on this page were created with COMSOL Multiphysics 6.2.

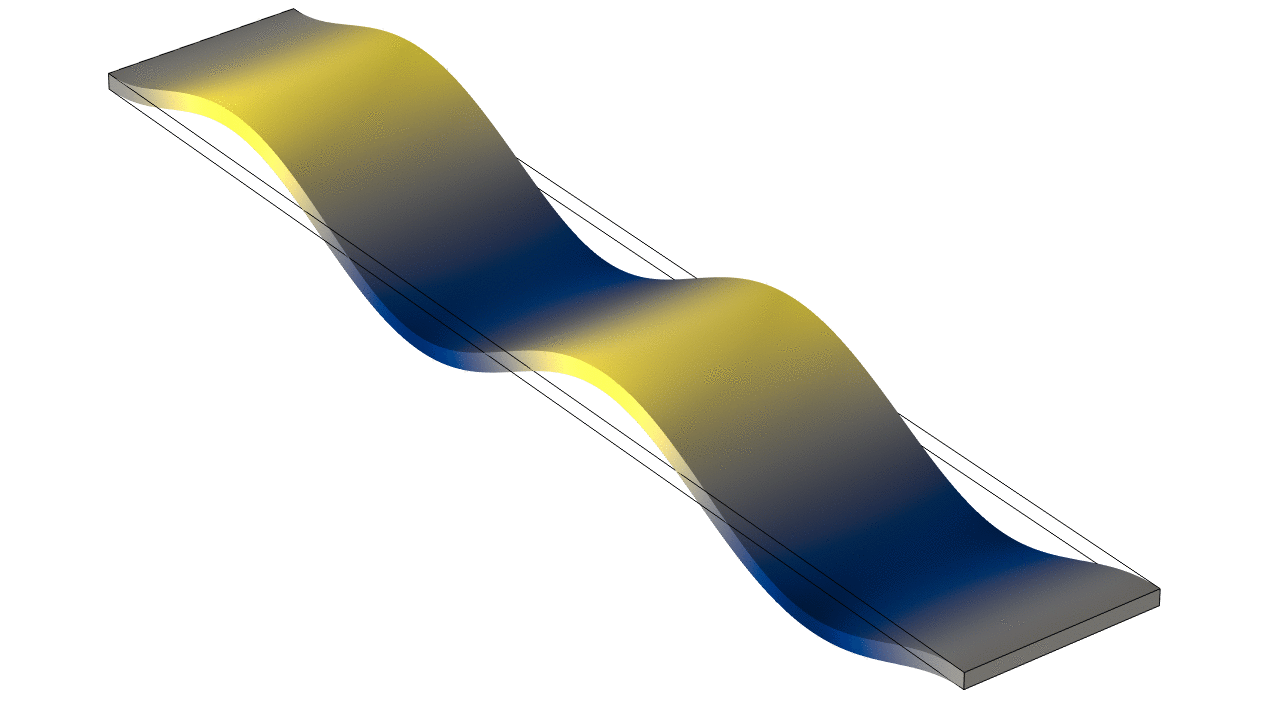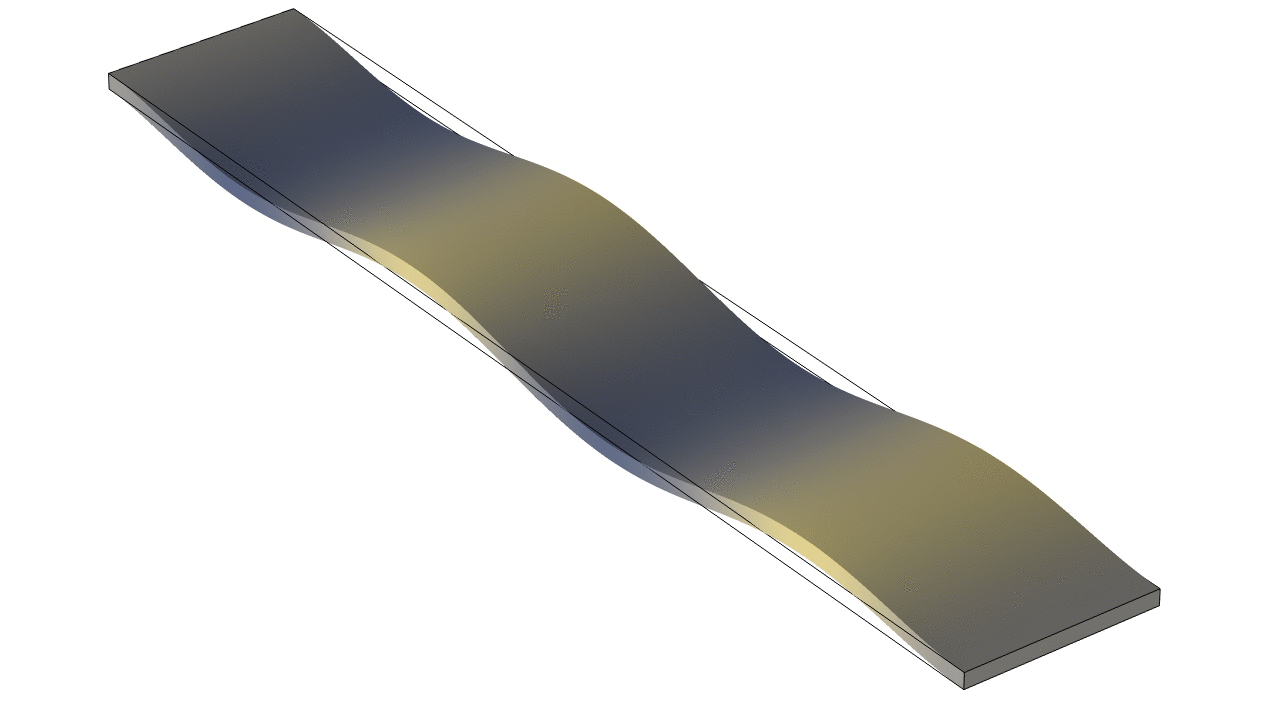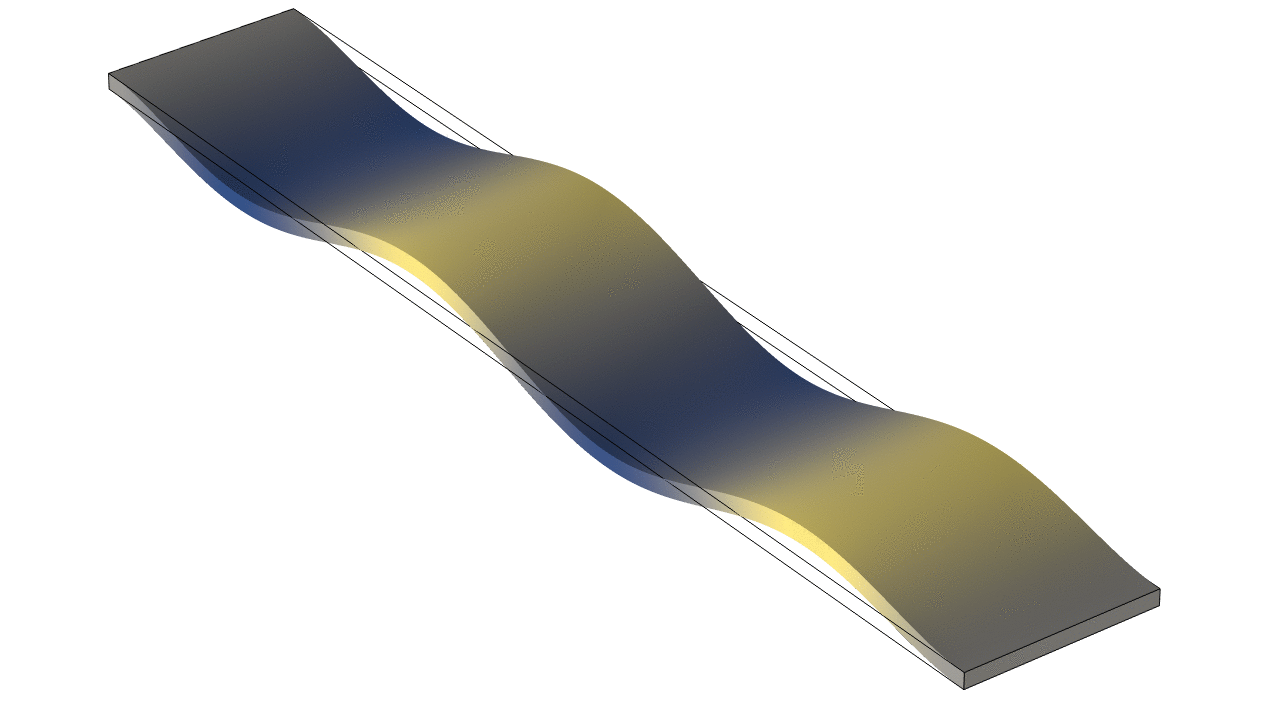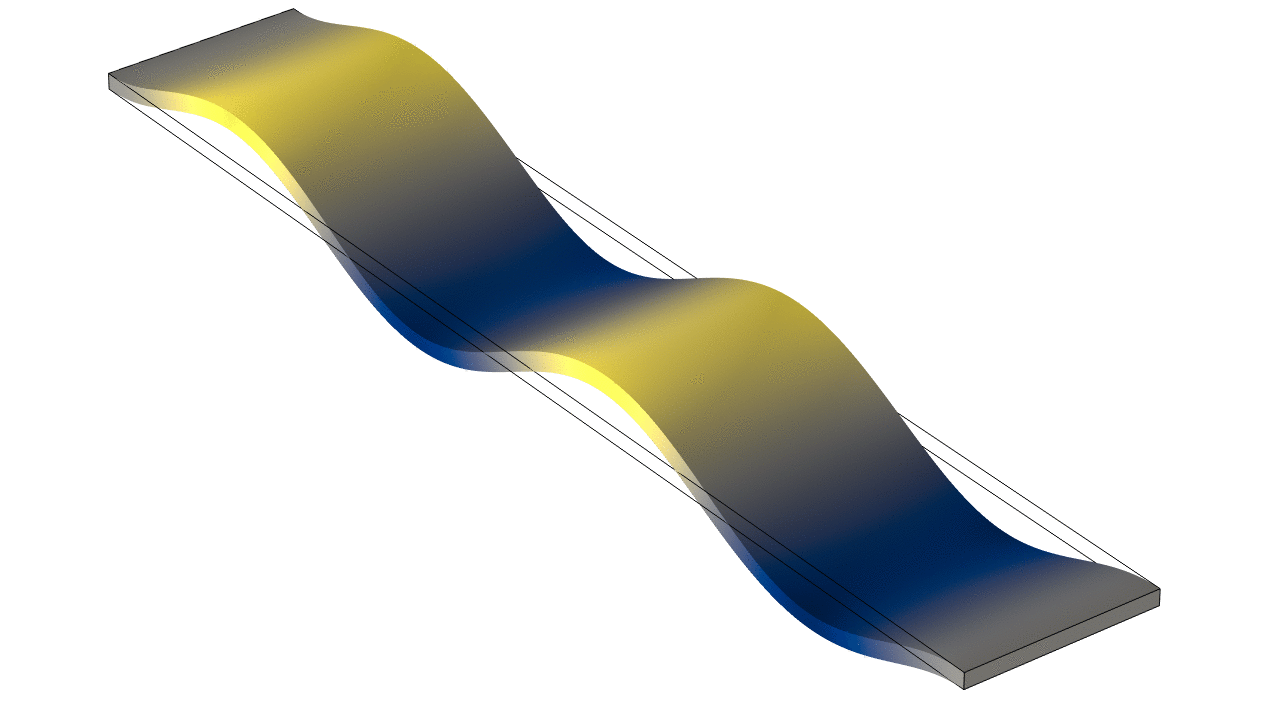
Thin Rectangular Bar Free At Both Ends (Free-Free)

The animations below show the first five mode shapes for an Aluminum Bar (5 cm wide, 30 cm long, and 4 mm thick), free at both ends. The flexural fending frequencies for a thin bar free at both ends may be accurately approximated by $$ f = \frac{\pi}{8}\frac{h}{\sqrt{12}}\frac{1}{L^2}\sqrt{\frac{E}{\rho}}\;(2n+1)^2 $$ where \(h\) and \(L\) are the thickness and length of the bar, respectively and \(E\) is the Young's elastic modulus and \(\rho\) is the density. The frequencies depend on mode number \(n\) as \((2n+1)^2\) so that the frequencies are not integer multiples of a fundamental, as they are for longitudinal waves in a bar or transverse waves on a string.

Animation showing the first flexural bending mode for a free-free bar. The two colors indicate motion in opposite directions. The first mode has two nodal line across the width of the bar at the roughly a fourth of the length from each end.
Animation showing the second flexural bending mode for a free-free bar. The two colors indicate motion in opposite directions. The second mode has three nodal lines across the width of the bar.
Animation showing the third flexural bending mode for a free-free bar. The two colors indicate motion in opposite directions. The third mode has four nodal lines across the width of the bar.
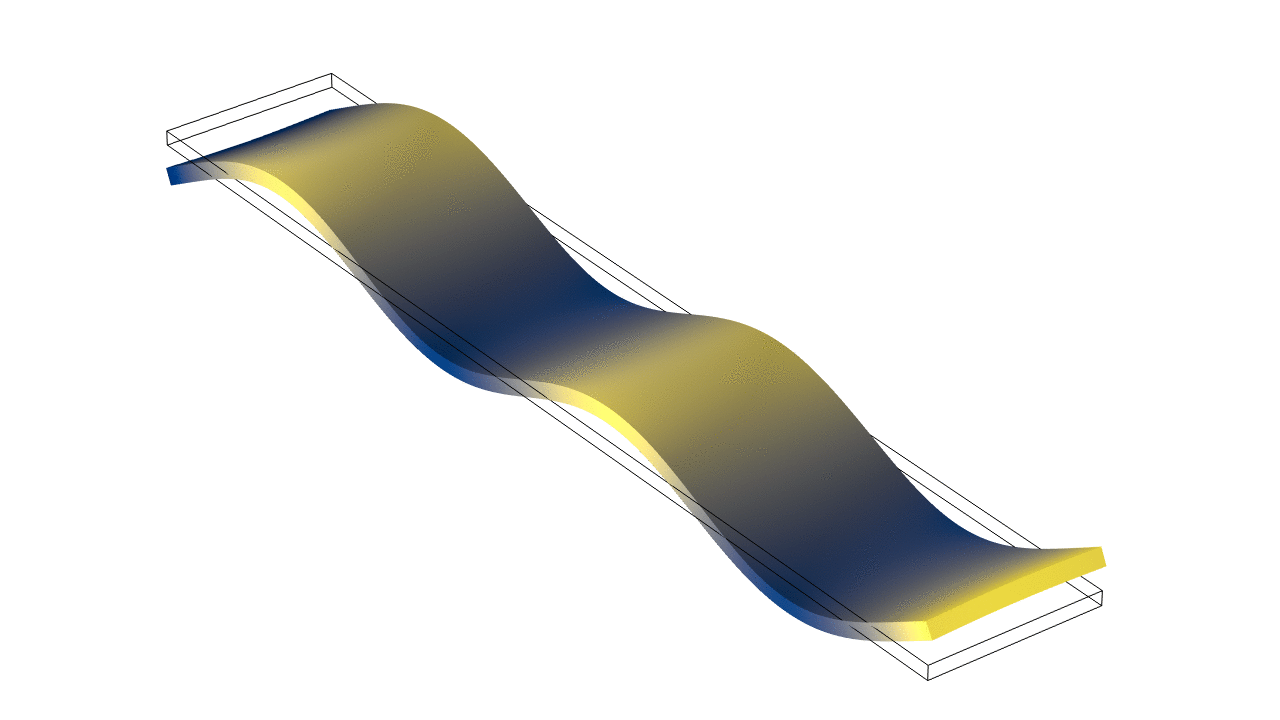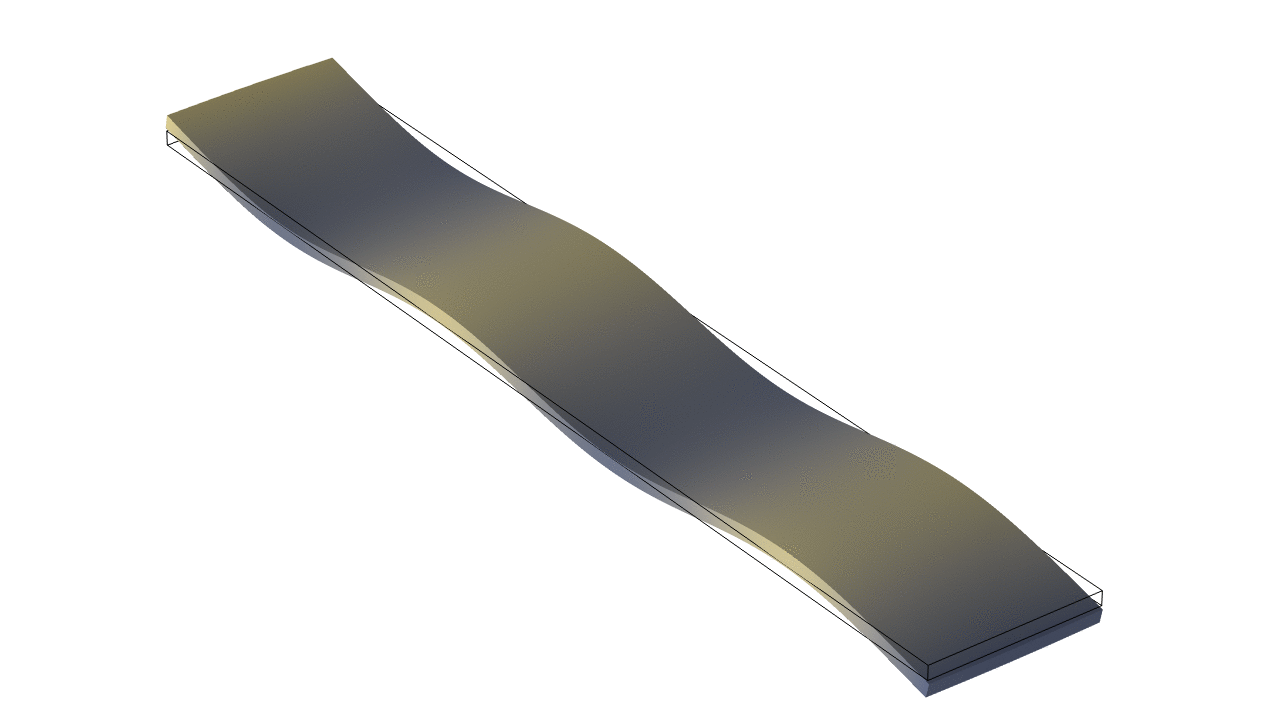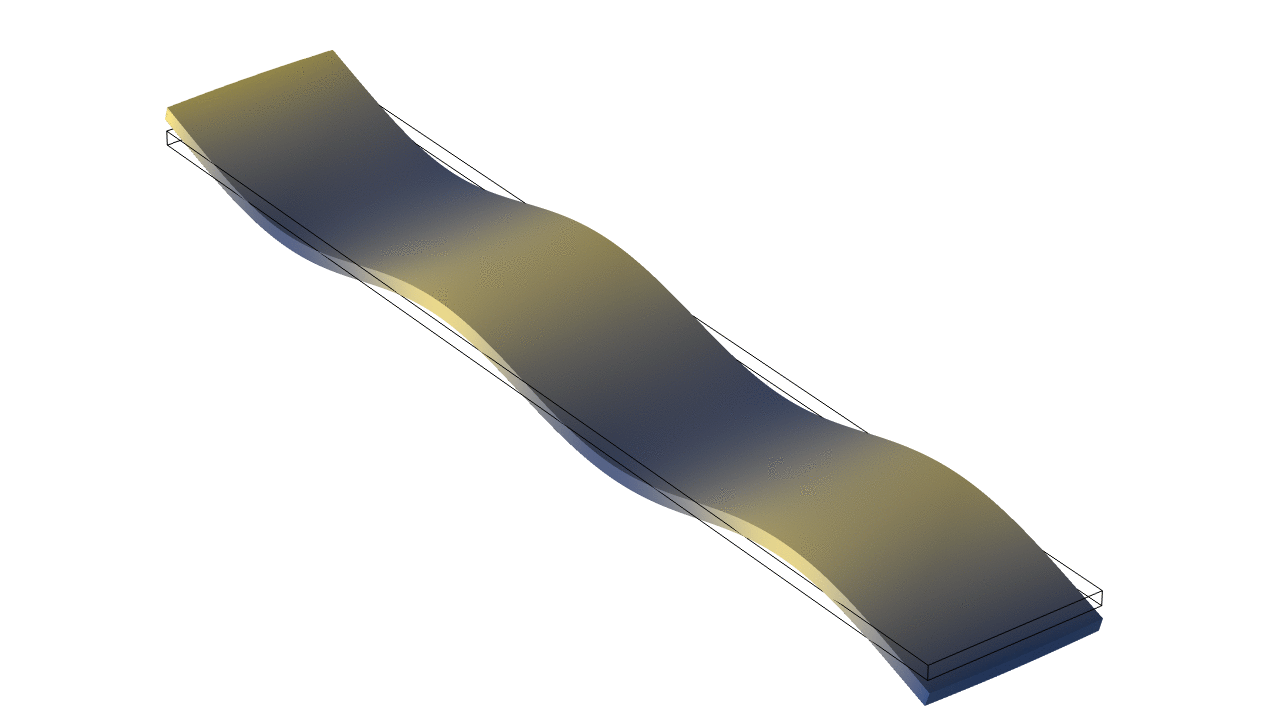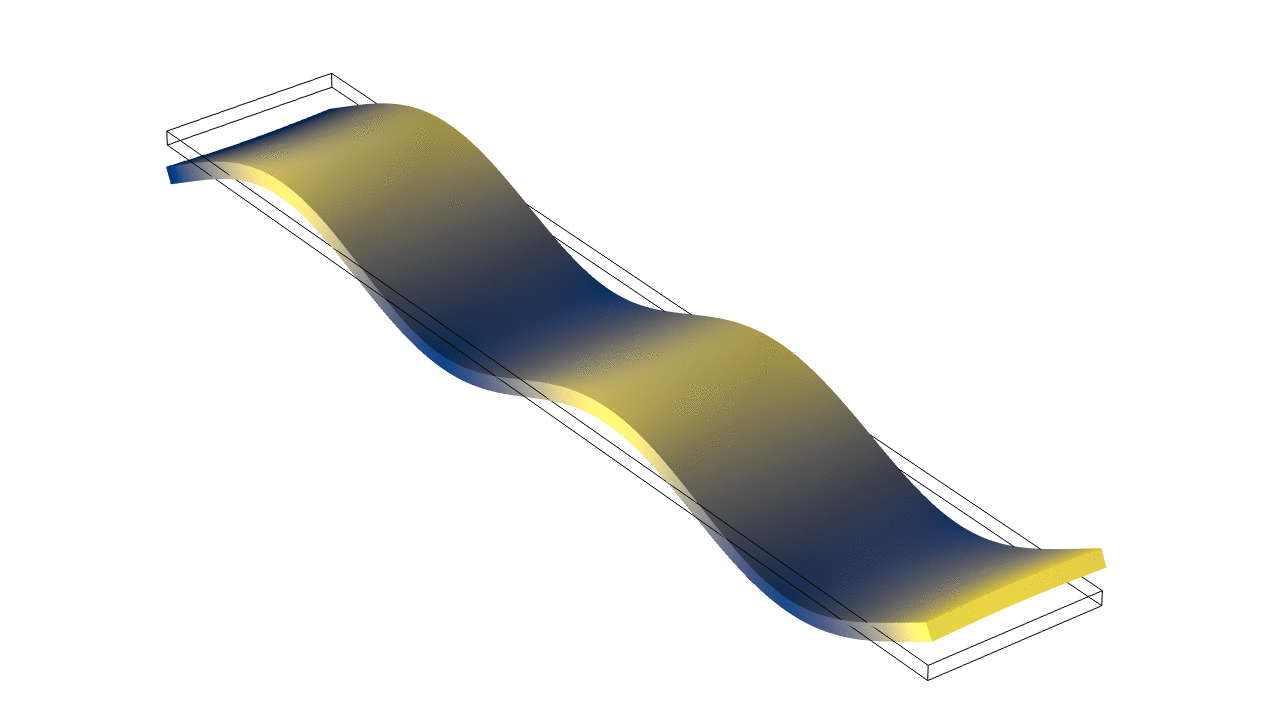
Animation showing the fourth flexural bending mode for a free-free bar. The two colors indicate motion in opposite directions). The fourth mode has four nodal lines across the width of the bar.
Animation showing the fifth flexural bending mode for a free-free bar. The two colors indicate motion in opposite directions. The fifth mode has five nodal lines across the width of the bar.
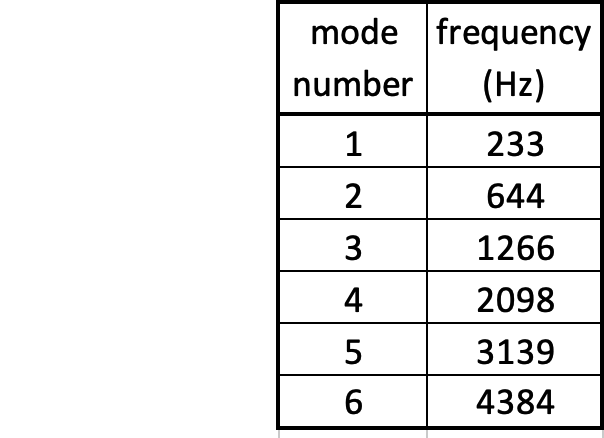
Table showing the frequencies for the flexural bending modes for a free-free bar: first mode at 233 Hz, second mode at 644 Hz, third mode at 1266 Hz, fourth mode at 2098 Hz, and fifth mode at 3139 Hz.

Thin Rectangular Bar Fixed At Both Ends (Fixed-Fixed)

The animations below show the first five mode shapes for an Aluminum Bar (5 cm wide, 30 cm long, and 4 mm thick), fixed at both ends. When using the Bernoulli-Euler approximate theory for flexural waves in a thin bar, the frequencies for a thin bar fixed at both ends are practically identical to those for a free-free bar with the same dimensions and material properties (equation given above). In reality, there are slight differences between the frequencies for the two boundary conditions, which become more divergent when the thickness increases.

Animation showing the first flexural bending mode for a free-free bar. Red and blue colors indicate motion in opposite directions (red is up and blue is down). The first mode has two nodal line across the width of the bar at the roughly a fourth of the length from each end.
Animation showing the second flexural bending mode for a free-free bar. Red and blue colors indicate motion in opposite directions (red is up and blue is down). The second mode has three nodal lines across the width of the bar.
Animation showing the third flexural bending mode for a free-free bar. Red and blue colors indicate motion in opposite directions (red is up and blue is down). The third mode has four nodal lines across the width of the bar.
Animation showing the fourth flexural bending mode for a free-free bar. Red and blue colors indicate motion in opposite directions (red is up and blue is down). The fourth mode has four nodal lines across the width of the bar.
Animation showing the fifth flexural bending mode for a free-free bar. Red and blue colors indicate motion in opposite directions (red is up and blue is down). The fifth mode has five nodal lines across the width of the bar.
Table showing the frequencies for the flexural bending modes for a fixed-fixed bar: first mode at 238 Hz, second mode at 655 Hz, third mode at 1284 Hz, fourth mode at 2117 Hz, and fifth mode at 3169 Hz.

Some examples of vibrating objects which exhibit Flexural Bending oscillation

Some examples of vibrating objects which exhibit Flexural Bending oscillation