Acoustics and Vibration Animations
Daniel A. Russell, Ph.D.
Graduate Program in Acoustics
The Pennsylvania State University
All text and images on this page are ©2004-2011 by Daniel A. Russell
and may not used in other web pages or reports without permission.

Superposition of Waves

The principle of superposition may be applied to waves whenever two (or more) waves travelling through the same medium at the same time. The waves pass through each other without being disturbed. The net displacement of the medium at any point in space or time, is simply the sum of the individual wave displacements. This is true of waves which are finite in length (wave pulses) or which are continuous sine waves.

Superposition of two opposite direction wave pulses

The animation at right shows two Gaussian wave pulses are travelling in the same medium, one is moving to the right, the other is moving to the left. The two waves pass through each other without being disturbed, and the net displacement is the sum of the two individual displacements.

It should also be mentioned that this medium is nondispersive (all frequencies travel at the same speed) since the Gaussian wave pulses do not change their shape as they propagate. If the medium was dispersive, then the waves would change their shape.

Solitons are examples of nonlinear waves that do not obey the principle of superposition when they interact with each other.

Constructive and Destructive Interference

Two waves (with the same amplitude, frequency, and wavelength) are travelling in the same direction on a string. Using the principle of superposition, the resulting string displacement may be written as:

which is a travelling wave whose amplitude depends on the phase (phi). When the two waves are in-phase (phi=0), they interfere constructively and the result has twice the amplitude of the individual waves. When the two waves have opposite-phase (phi=180), they interfere destructively and cancel each other out.

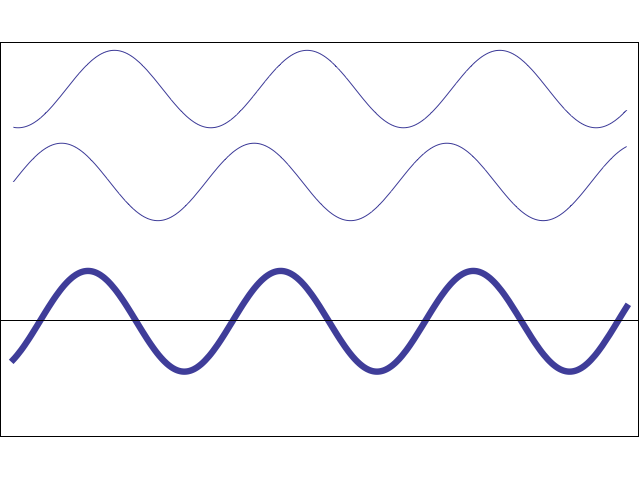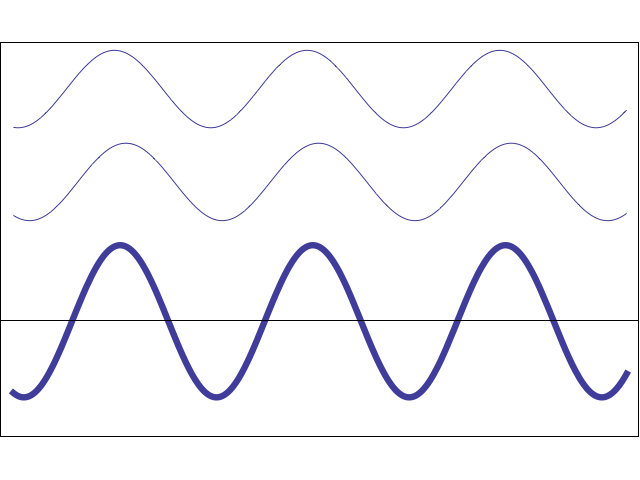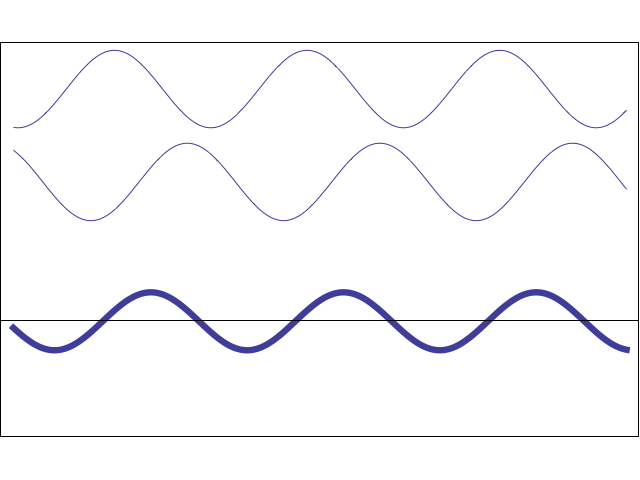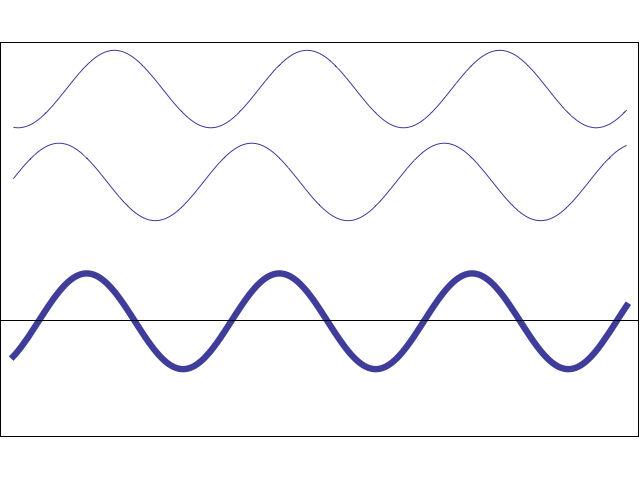The animation at left shows how two sinusoidal waves with the same amplitude and frequency can add either destructively or constructively depending on their relative phase. (NOTE: this animation does not depict the propagation of actual waves in a medium - it only serves to illustrate the effect of changing the phase shift between two waves and the resulting constructive or destructive interference). The phase difference between the two waves increases with time so that the effects of both constructive and destructive interference may be seen. When the two individual waves are exactly in phase the result is large amplitude. When the two gray waves become exactly out of phase the sum wave is zero.

Two sine waves travelling in opposite directions create a standing wave

A travelling wave moves from one place to another, whereas a standing wave appears to stand still, vibrating in place. Two waves (with the same amplitude, frequency, and wavelength) are travelling in opposite directions on a string. Using the principle of superposition, the resulting string displacement may be written as:

This wave is no longer a travelling wave because the position and time dependence have been separated. The displacement of the string as a function of position has an amplitude of 2y_msin(kx). This amplitude does not travel along the string, but stands still and oscillates up and down according to cos(ω t). Characteristic of standing waves are locations with maximum displacement (antinodes) and locations with zero displacement (nodes).

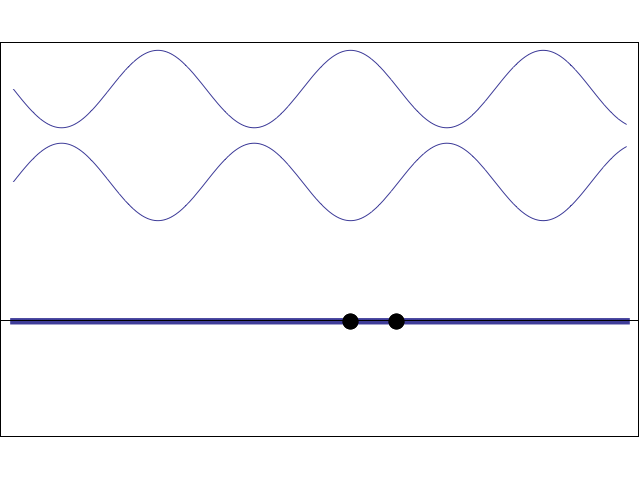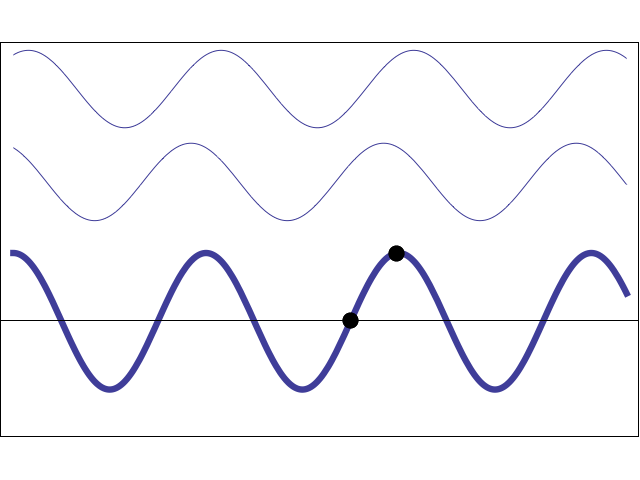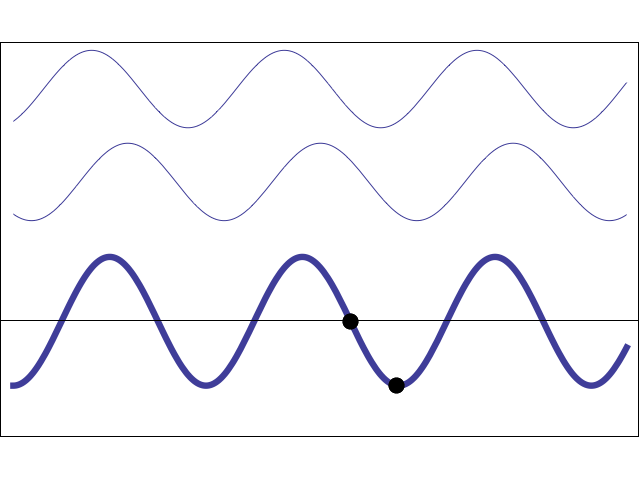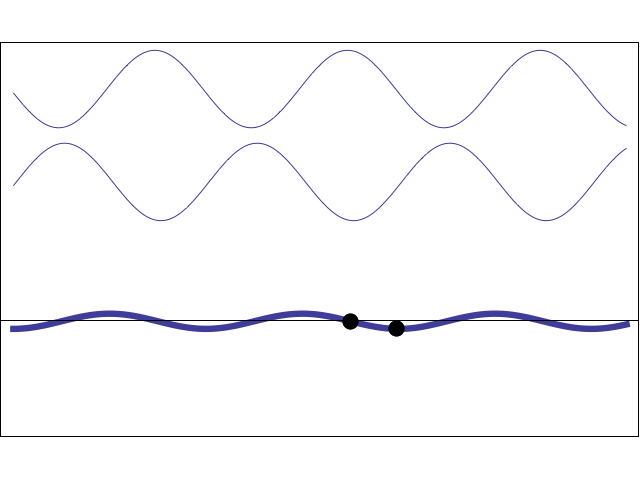The movie at left shows how a standing wave may be created from two travelling waves. If two sinusoidal waves having the same frequency (and wavelength) and the same amplitude are travelling in opposite directions in the same medium then, using superposition, the net displacement of the medium is the sum of the two waves. As the movie shows, when the two waves are 180° out-of-phase with each other they cancel, and when they are exactly in-phase with each other they add together. As the two waves pass through each other, the net result alternates between zero and some maximum amplitude. However, this pattern simply oscillates; it does not travel to the right or the left, and thus it is called a "standing wave".
I have placed two dots on the string, one at an antinode and one at a node. Which is which?
Check out my related animation to see how standing waves may be created in a medium due to reflection of a wave from a boundary.

Two sine waves with different frequencies: Beats

Two waves of equal amplitude are travelling in the same direction. The two waves have different frequencies and wavelengths, but they both travel with the same wave speed. Using the principle of superposition, the resulting particle displacement may be written as:

This resulting particle motion is the product of two travelling waves. One part is a sine wave which oscillates with the average frequency f = ½(f₁ + f₂). This is the frequency which is perceived by a listener. The other part is a cosine wave which oscillates with the difference frequency f = ½(f₁ - f₂). This term controls the amplitude "envelope" of the wave and causes the perception of "beats". The beat frequency is actually twice the difference frequency, f_beat = (f₁ - f₂).

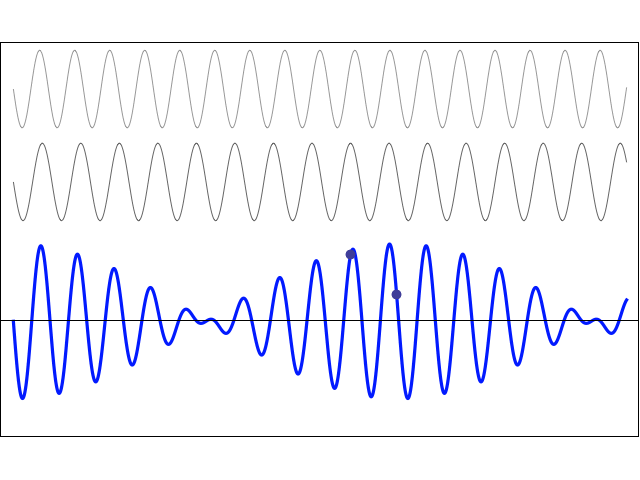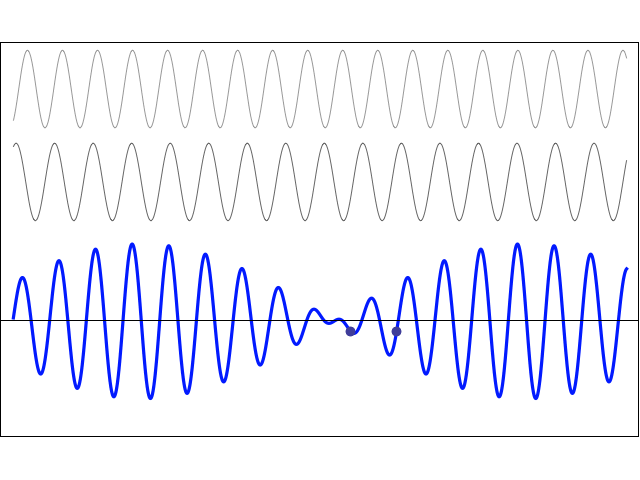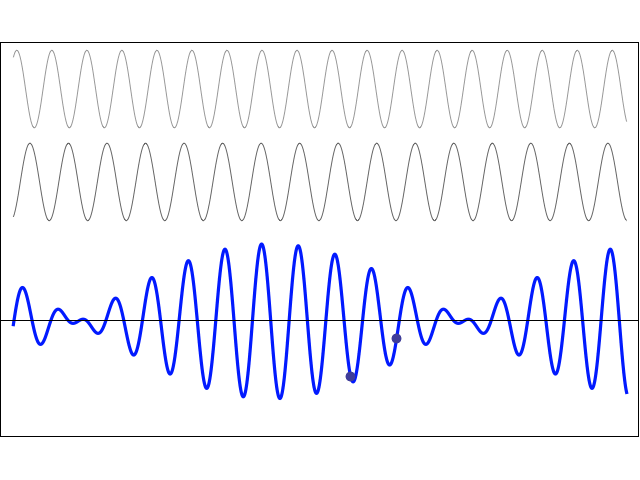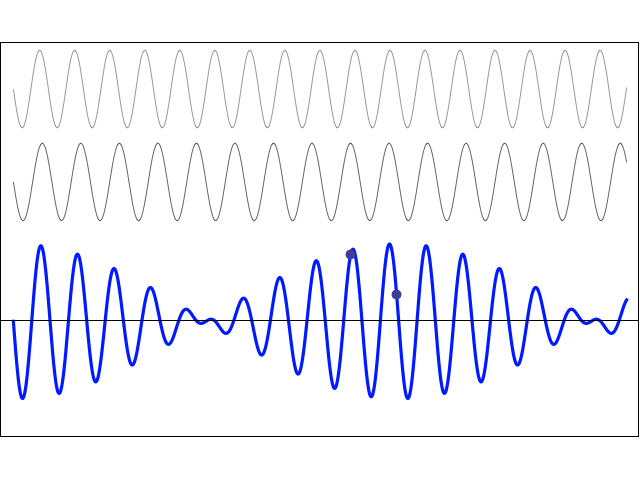In the movie at right two waves with slightly different frequencies are travelling to the right. Since the two waves are travelling in the same medium, they travel with the same speed. The resulting superposition sum wave travels in the same direction and with the same speed as the two component waves, but its local amplitude depends on whether the two individual waves have the same or opposite phase. The "beat" wave oscillates with the average frequency, and its amplitude envelope varies according to the difference frequency.

Back to the Vibrations and Waves: Demos and Animations Page