Waves in a Dispersive Medium

Dispersion causes the shape of a wave pulse to change as it travels

animation showing two pulses traveling; one pulse maintains a constant height and width while the other pulse widens and decreases in amplitude as it travels.

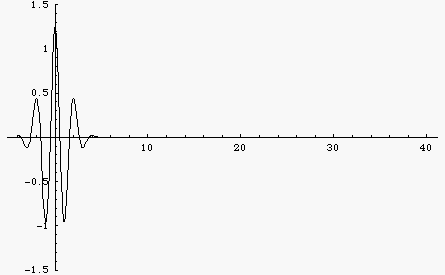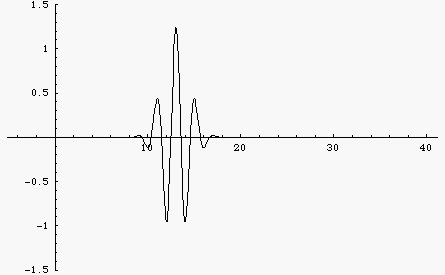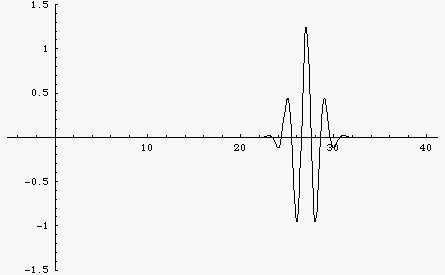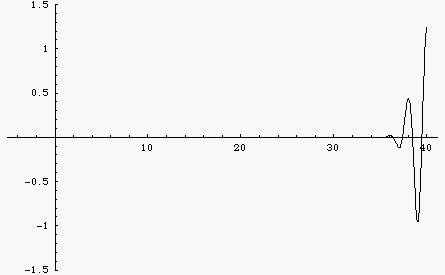
If the wave speed depends only on the physical properties of the medium (i.e., the elastic and inertia properties of a mechanical medium, or the relative permeability and permittivity for EM waves) then the wave speed is a constant, independent of frequency. Such a medium is called a non-dispersive medium and waves traveling through this medium will maintain a constant shape. This is illustrated by the black wave pulse in the animation at left. The pulse is a Gaussian function, containing multiple frequencies. Since the wave speed is constant, all frequencies travel at the same speed and the pulse maintains constant shape.

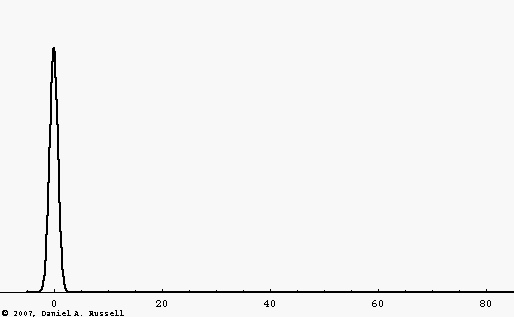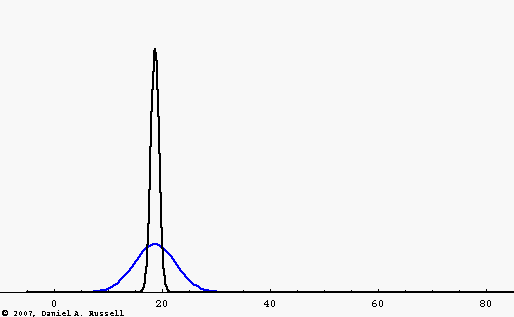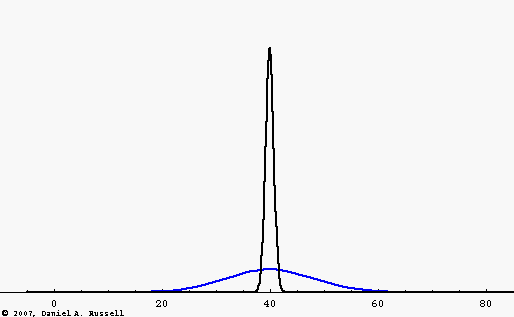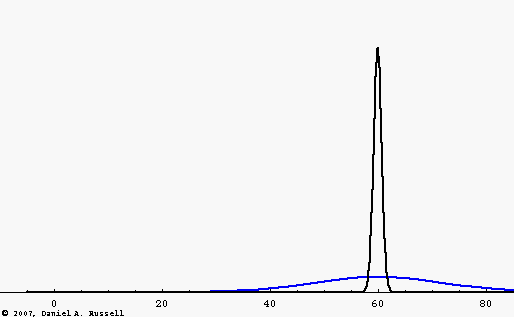
However, there are many examples of dispersive media where, for various reasons, the wave speed depends on the frequency of the wave. The blue wave pulse in the animation is the same Gaussian function as the black pulse, consisting of a large number of frequency components added together. However, now the wave speed depends on frequency, with higher frequencies traveling faster than lower frequencies. As a result, the wave pulse spreads out and changes shape as it travels.

The "mid-point" of both wave pulses travel at the same speed. This fact leads to the concept of a "group velocity" which is the speed with which the energy carried by the wave travels. The group velocity is the same for each wave pulse.

Dispersion for a wave packet with many frequency components

animation showing that a wave packet traveling in a non-dispersive medium does not change shape as it travels.

The animation at left shows a wave packet built up from a sum of 100 cosine functions with different frequencies. In a non-dispersive medium all of the different frequency components travel at the same speed so the wave function doesn't change at all as it travels.

animation showing that a wave packet traveling in a dispersive medium changes shape as it travels because higher frequency components travel at different speeds than lower frequency components.

Here is the same wave packet, built up from a sum of 100 cosine functions with different frequencies. But now the medium is dispersive so that different frequency components travel at different speeds. Now the wave changes shape. You can see the group velocity (envelope) and the phase velocity. For this example, the dispersion is such that lower frequencies travel faster than higher frequencies. As a result, the wave packet spreads out with the longer wavelengths moving faster and the shorter wavelengths lagging behind.