A string which is fixed at both ends will exhibit strong vibrational response only at the resonance frequncies
The vibrational pattern (mode shape) of the string at resonance will have the form

|
When a fixed-fixed string is set into vibration by plucking it, the string will vibrate at many of its natural resonance frequencies at the same time. Exacly which resonance frequencies (and thus which mode shapes) make up the final string vibration depends on the shape of the initial string displacement. The movie at left (0.58MB mpeg) shows the vibration of a fixed-fixed string which has been plucked at a point 1/3 of its length from the left end (x = 1/3L). As you observe the vibration you should be able to visualize two wave pulses, one travelling clockwise, the other travelling counterclockwise. The time for one complete trip equals one period - if the string wave vibrating with a fundamental frequency of 440 Hz, then this vibration cycle would repeat itself 440 times per second.
|
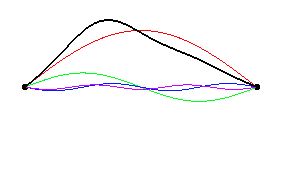 Fourier's theorem says that any periodic function f(t) may be constructed from a combination of sin(w t) and cos(w t) functions with appropriate amplitudes and frequencies. The picture at left shows the amplitude and phase of the first 6 string modes which add up to produce the initial string position (plucked at x = 1/3L). [color code: sum, n=1, n=2, n=3, n=4, n=5, n=6 ] You should notice that modes corresponding to n=3 and n=6 are missing. This is because standing wave patterns which have a node at the pluck point will not be excited. Since any mode which is an integer multiple of n=3 will have a node at position x=L/3 these standing wave patterns will not be excited. Fourier's theorem says that any periodic function f(t) may be constructed from a combination of sin(w t) and cos(w t) functions with appropriate amplitudes and frequencies. The picture at left shows the amplitude and phase of the first 6 string modes which add up to produce the initial string position (plucked at x = 1/3L). [color code: sum, n=1, n=2, n=3, n=4, n=5, n=6 ] You should notice that modes corresponding to n=3 and n=6 are missing. This is because standing wave patterns which have a node at the pluck point will not be excited. Since any mode which is an integer multiple of n=3 will have a node at position x=L/3 these standing wave patterns will not be excited.
|
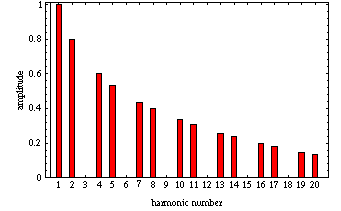 A "frequency spectrum" may be constructed for this plucked string vibration by determining the standing wave mode number (resonance frequency) and amplitude for all mode shapes which are present in a given string vibraiton. The figure at left shows the mode number spectrum for the string struck at (plucked at x = 1/3L). Notice that all multiples of 3 are missing. A "frequency spectrum" may be constructed for this plucked string vibration by determining the standing wave mode number (resonance frequency) and amplitude for all mode shapes which are present in a given string vibraiton. The figure at left shows the mode number spectrum for the string struck at (plucked at x = 1/3L). Notice that all multiples of 3 are missing.
|


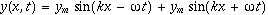

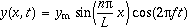 .
. 


 A "frequency spectrum" may be constructed for this plucked string vibration by determining the standing wave mode number (resonance frequency) and amplitude for all mode shapes which are present in a given string vibraiton. The figure at left shows the mode number spectrum for the string struck at (plucked at x = 1/3L). Notice that all multiples of 3 are missing.
A "frequency spectrum" may be constructed for this plucked string vibration by determining the standing wave mode number (resonance frequency) and amplitude for all mode shapes which are present in a given string vibraiton. The figure at left shows the mode number spectrum for the string struck at (plucked at x = 1/3L). Notice that all multiples of 3 are missing.