On the Sound Field Radiated by a Tuning Fork
The animations on this page were created to accompany the following article:
- Daniel A. Russell, "On the sound field radiated by a tuning fork," Am. J. Phys. 68(12), 1139-1145 (2000).
You can download a PDF copy of the paper "On the sound field radiated by a tuning fork" or access the paper from the American Journal of Physics website (link opens in a new tab).
Animations to Accompany Specific Figures from the paper
Fig. 3: Sound field radiated by a cylinder whose radius oscillates according to \(R + \cos(2\theta)\sin(\omega t) \)
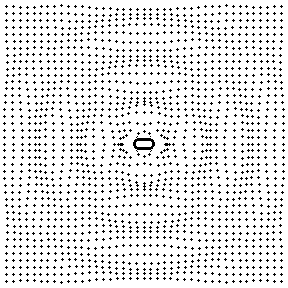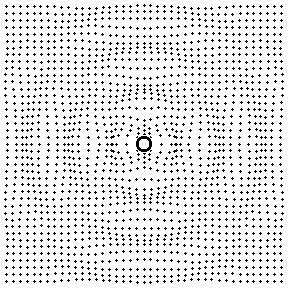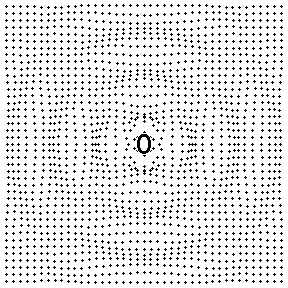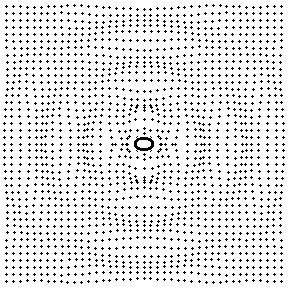
Excerpt from the text of the paper.....
The cylinder simultaneously elongates in the horizontal direction, pushing air outwards, and contracts in the vertical direction drawing air inwards. Half a cycle later the cylinder contracts in the horizontal direction drawing air inwards and expands in the vertical direction pushing air outwards............It is clear to see that waves propagating in the horizontal and vertical directions have opposite phase, and that the waves completely cancel along lines 45° from the horizontal.
Fig. 7: Contour plot of the pressure field produced by a longitudinal quadrupole
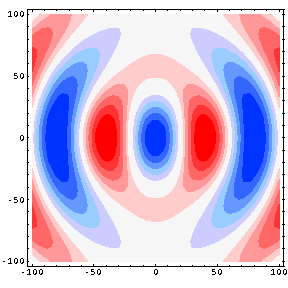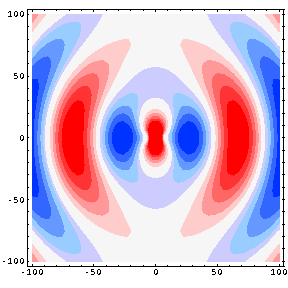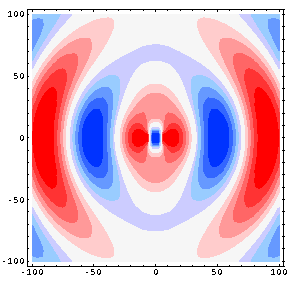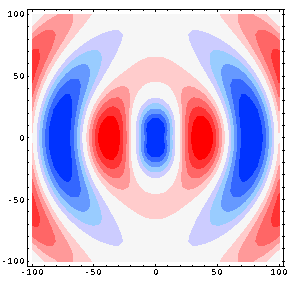
In the animation at left Red represents high pressure and Blue represents low pressure.
Excerpt from the text of the paper.....
The contour plot represents a 100 cm x 100 cm region with the source at the center of the plot; the two dipoles comprising the quadrupole , and representing the fork tines, are at ±1 cm. The animation is thus able to show both the near-field and far-field behavior of the pressure field. The wavelength is 80.5 cm, corresponding to a frequency of 426 Hz (the speed of sound is taken to be 343 m/s).
The contour plot (animation) shows both the near-field and far-field behavior of the pressure field......The transition from near-field to far-field is the result of a transition from path-length dependent amplitude differences to pathlength dependent phase differences. Consider the tuning fork as a linear quadrupole arrangement of four point sources. When the observer location is very close to the center of the fork, along a vertical orientation, the distance to the inner pair of (negative) sources is smaller than that to the outer (positive) pair. Since the pressure from a point source decreases as \( 1/r \) the pressure amplitude from the closer inner pair of sources dominates the near-field and a significant negative pressure is observed perpendicular to the source alignment. As one moves in the vertical direction away from the sources, the pathlength differences to each source become negligible and the phase differences dominate. Since there are an equal number of positive and negative sources, the pressures effectively cancel and there is very little resultant vertically propagating wave motion in the far-field.
The color palette used to generate this contour plot in Mathematica was borrowed from
V. W. Sparrow, J. L. Rochat, and B. A. Bard, "The use of color in the scientific visualization of acoustical phenomena," J. Comp. Acoust. 4(2), 202-223 (1996)
Fig. 12: Sound field produced by a dipole source
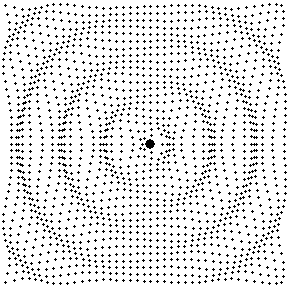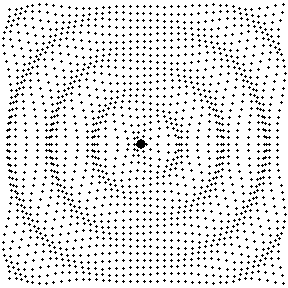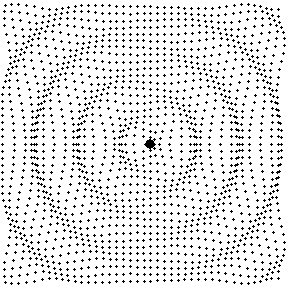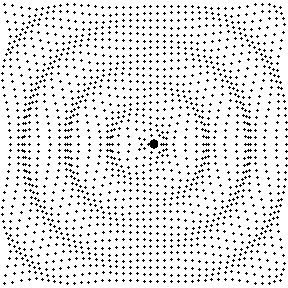
Excerpt from the text of the paper.....
Circular wave fronts with opposite phase are propagated left and right as the sphere moves back and forth in the horizontal direction. Fluid directly above and below the sphere sloshes back and forth as the sphere oscillates, but there is no wave propagation along the vertical axis of the figure.
Here is a link to my webpage showing animations of the Tuning Fork vibrational mode shapes that create these radiation patterns:
