Torsional Modes for a Rectangular Bar
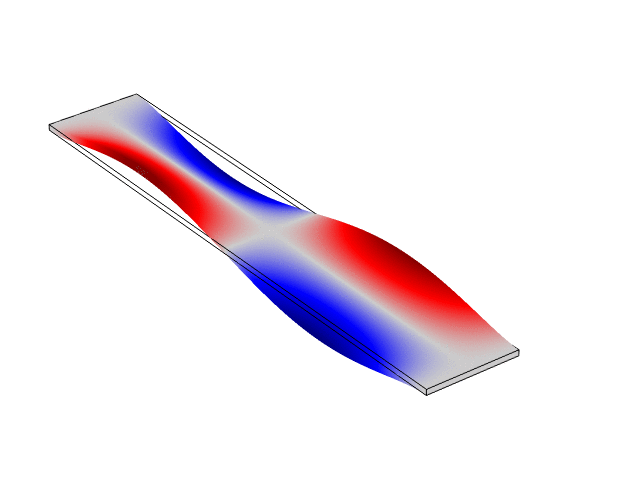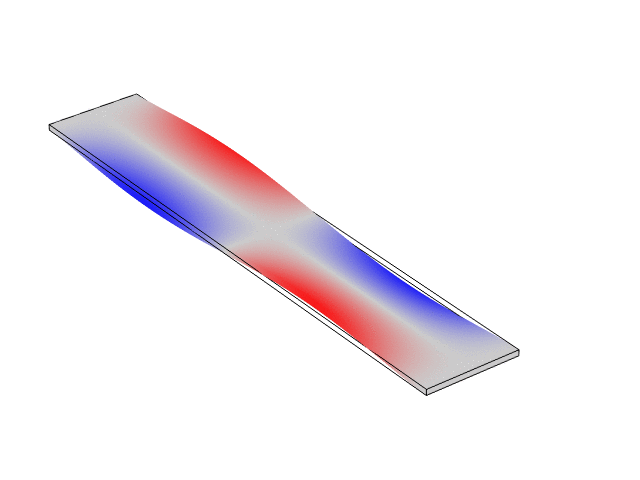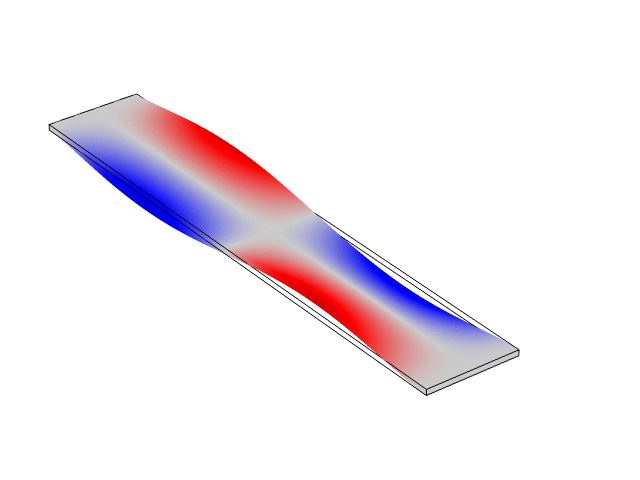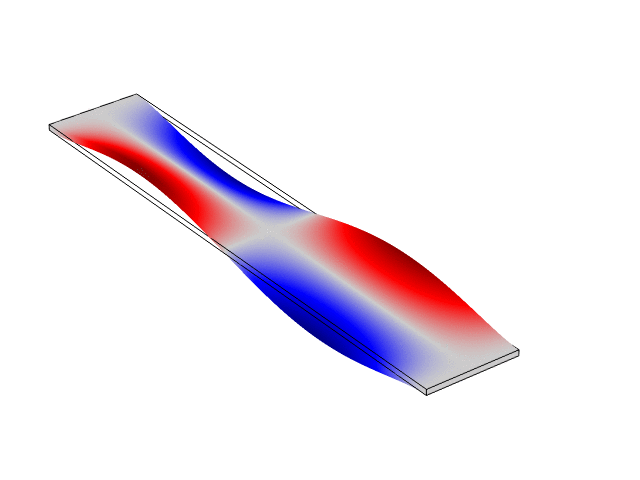
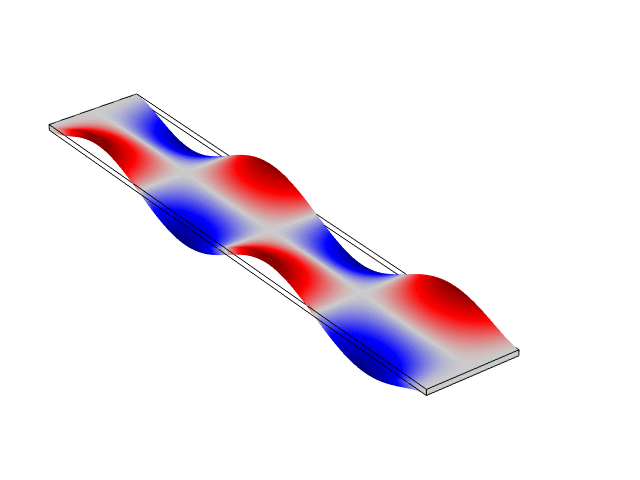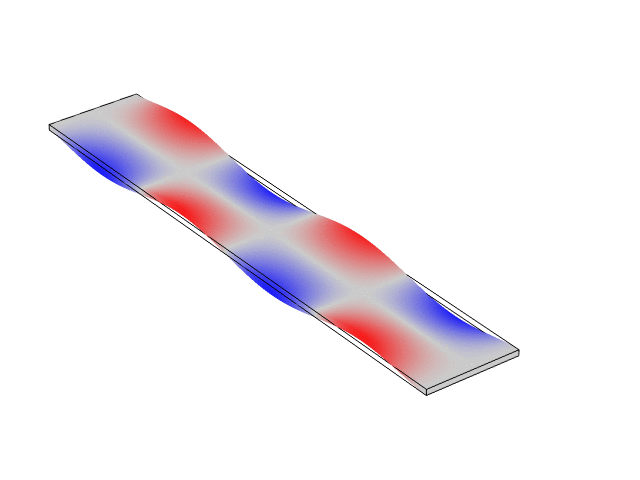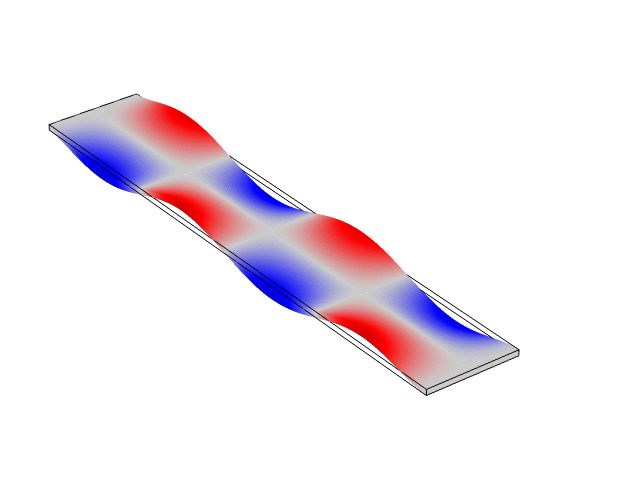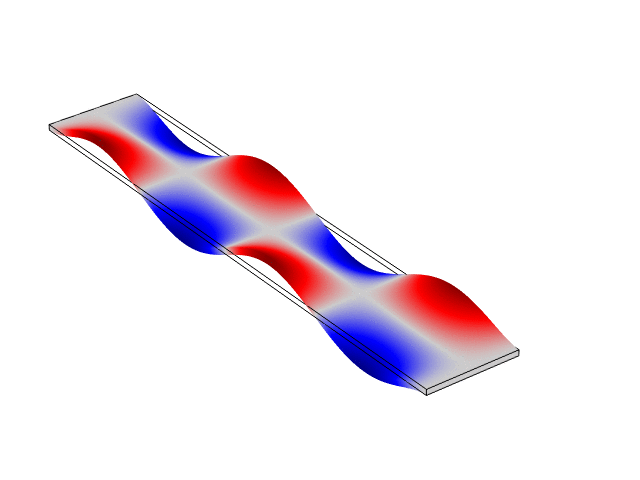
Rectangular Bar Free At Both Ends (Free-Free)
The animations below show the first five mode shapes for an Aluminum Bar (10 cm wide, 56 cm long, and 6 mm thick), free at both ends. These animations were created in COMSOL Multiphysics 6.1.


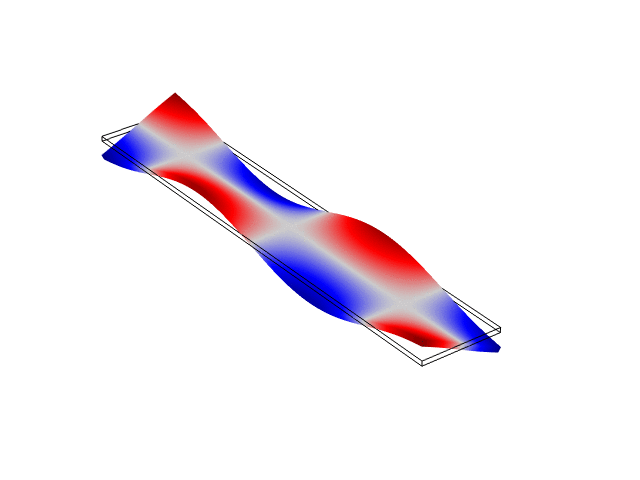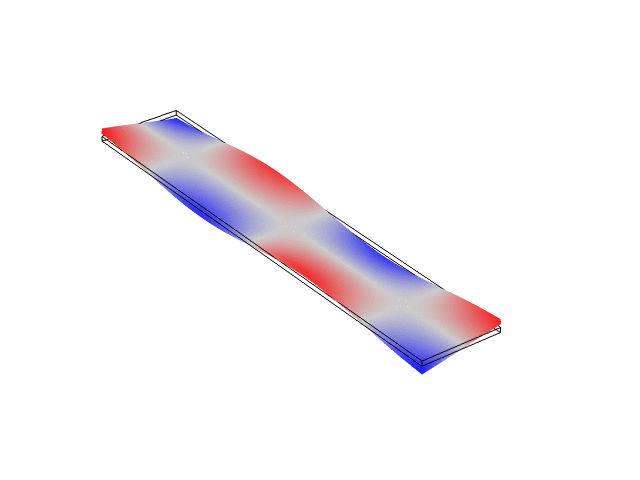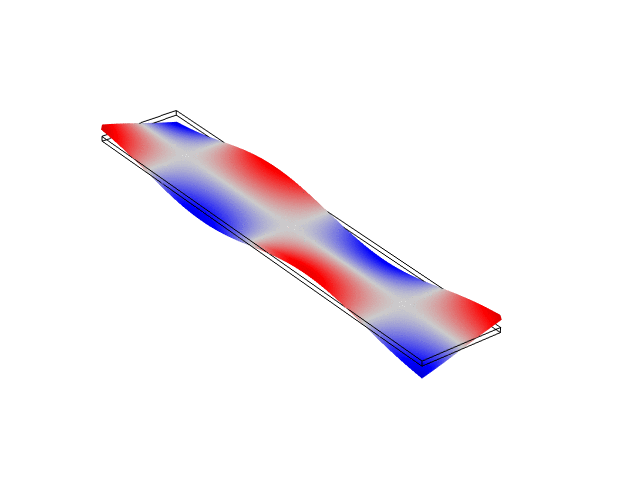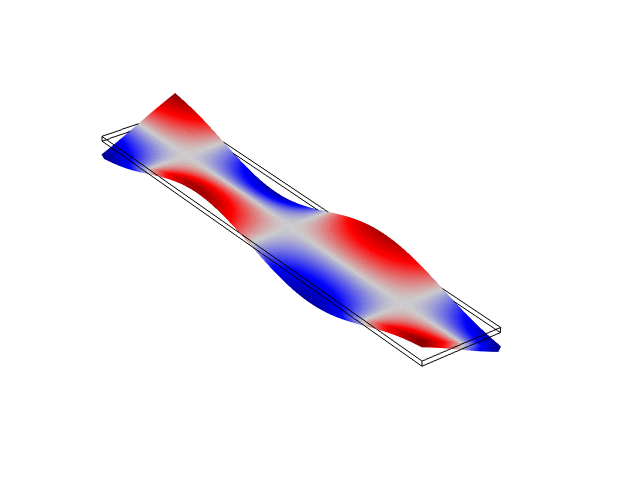
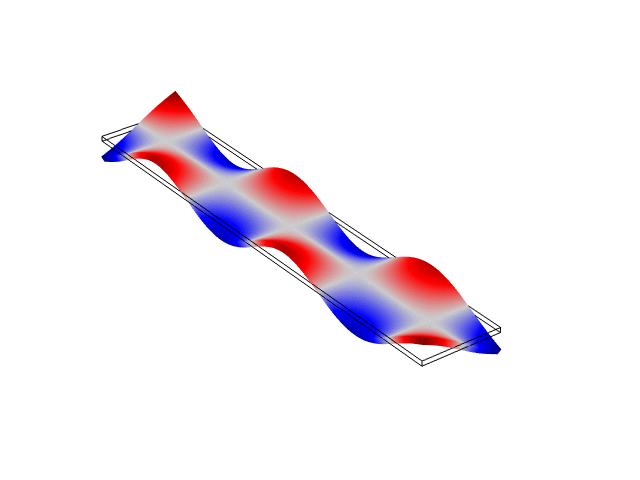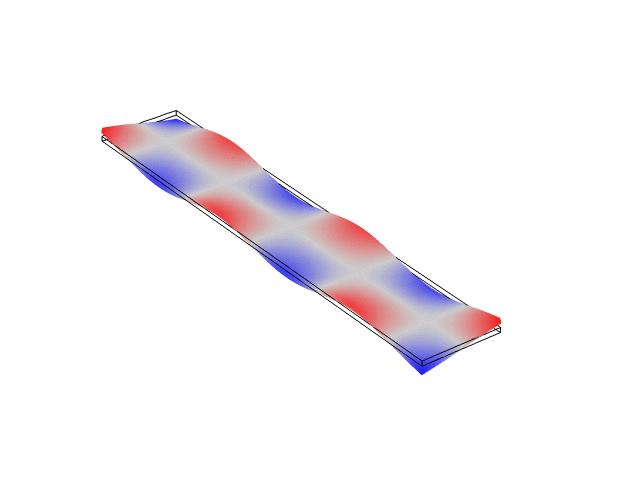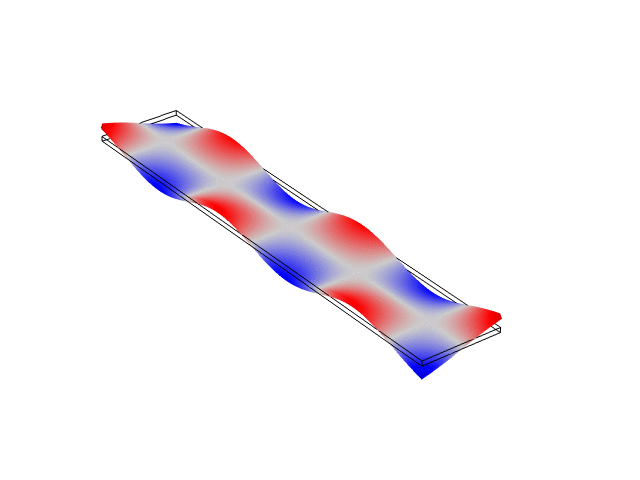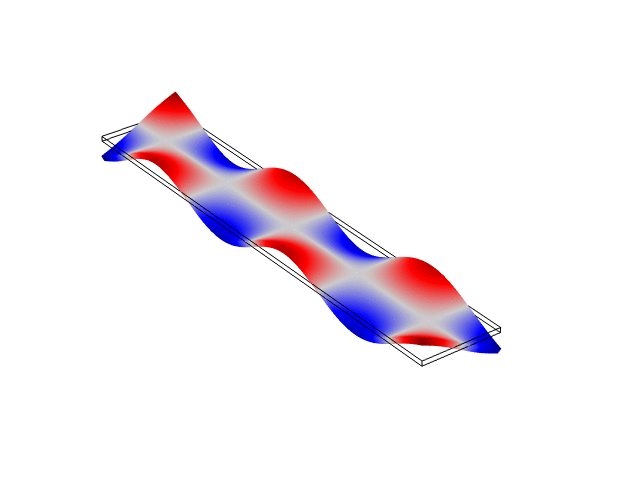
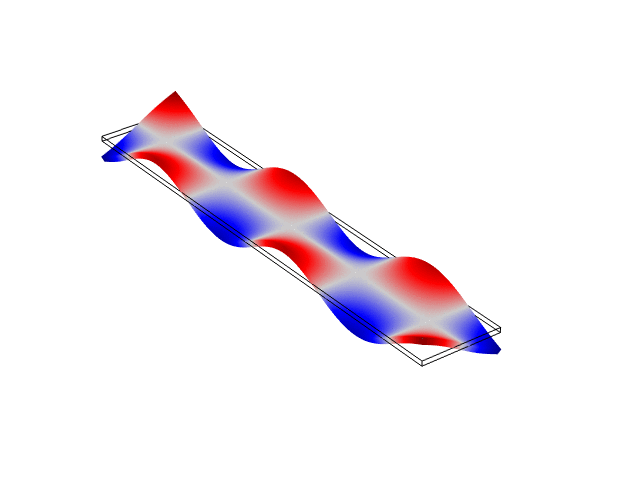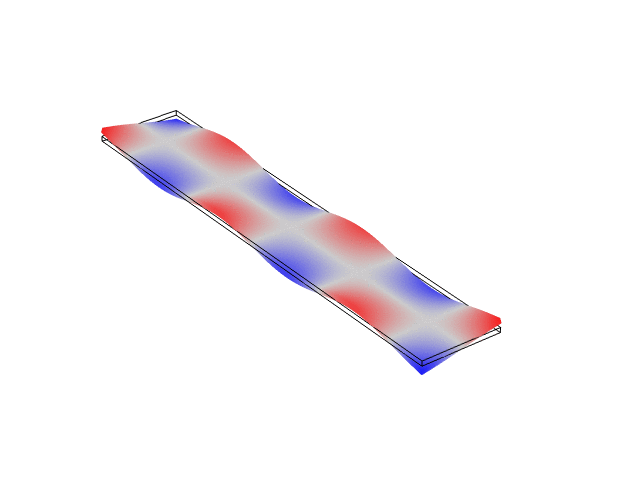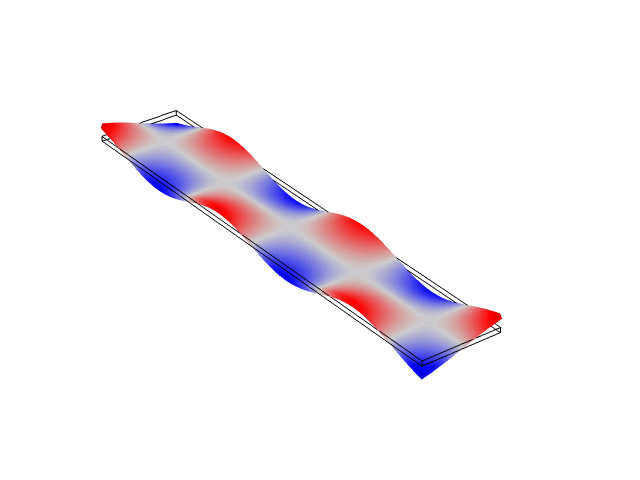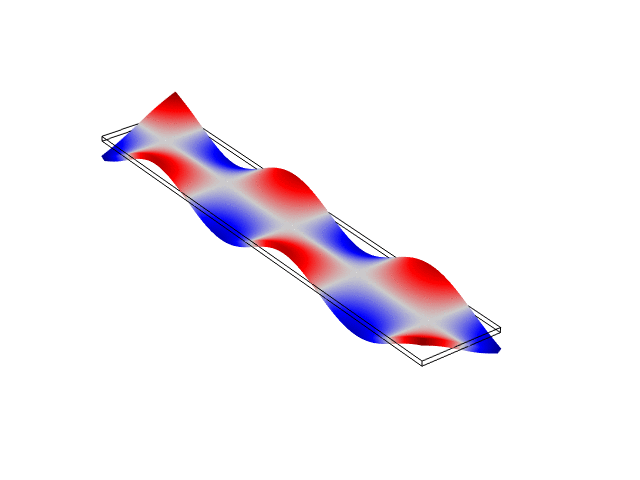
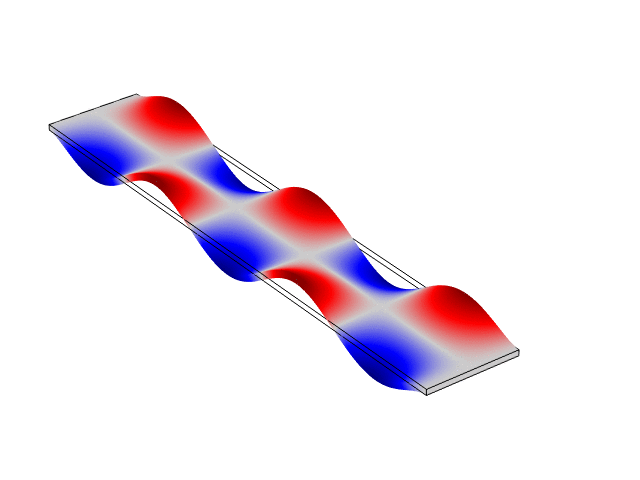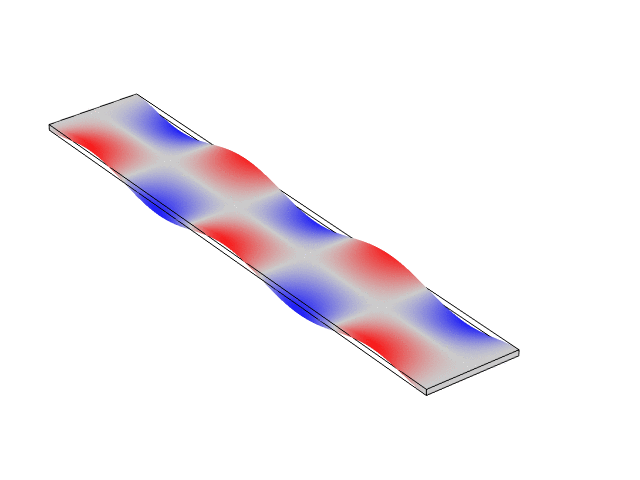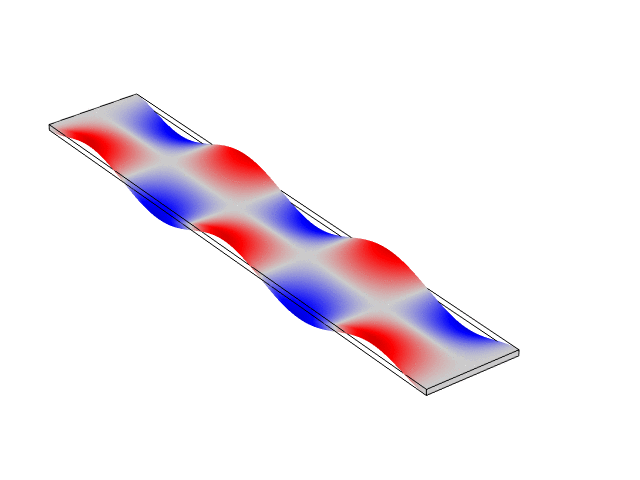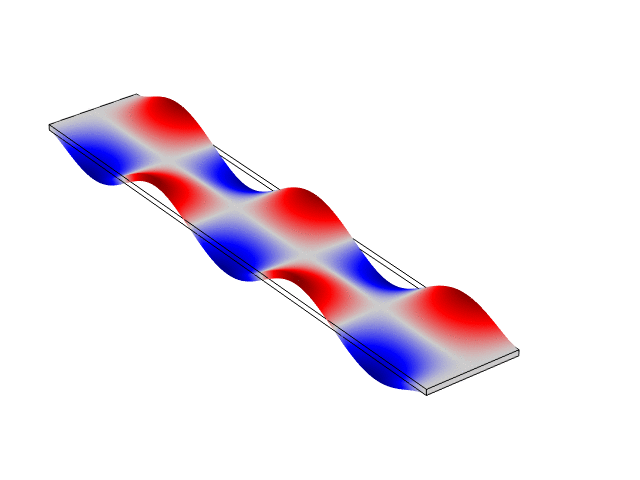
Rectangular Bar Fixed At Both Ends (Fixed-Fixed)
The animations below show the first five mode shapes for an Aluminum Bar (10 cm wide, 56 cm long, and 6 mm thick), fixed at both ends. These animations were created in COMSOL Multiphysics 6.1.


Theory and Background
The simple theory (which ignores the effects of warping and the coupling between bending and shear forces) for torsional or twisting oscillation in a bar/beam/rod results in an equation of motion for the angular displacement \(\theta\) of the cross-section of the bar from its equilibrium orientation, which has the form of the Wave Equation, $$ {\partial^2 \theta \over \partial x^2} - {1 \over c_T^2}{\partial^2 \theta \over \partial t^2} =0 \qquad \hbox{with} \qquad c_T = \sqrt{G K \over \rho I_p}$$ The wave speed \(c_T\) for torsional waves is depends on the material properties through the shear modulus, \(G\), which depends on Young's elastic modulus and Poisson's ratio \(\nu\) according to $$G = {Y \over 2 (1+\nu)} \; , $$ and the mass density \()\rho\) of the material from which the bar is made. The wave speed also depends on the shape and dimensions of the cross-sectional area. The factor \(K\) (units of \([\hbox{m}^4]\)) depends on the shape and dimensions of the cross-sectional area; for a bar with a rectangular cross-section of width \(w\) and height \(h\), $$ \hbox{rectangular cross-section of width $w$ and height $h$} \qquad \Longrightarrow \qquad K = {w h^3 \over 16} \Bigg[{16 \over 3} - 3.36 {h \over w}\bigg(1 - {h^4 \over 12 w^4}\bigg)\Bigg] \hskip50pt$$ $$\hbox{circular cross-section of radius $a$} \qquad \Longrightarrow \qquad K = {1 \over 2} \pi a^4 \hskip95pt$$ The quantity \(I_p\) (also with units of \([\hbox{m}^4]\)) represents the polar moment-of-inertia and depends on the shape and dimensions of the cross-sectional area: $$ \hbox{rectangular cross-section of width $w$ and height $h$} \qquad \Longrightarrow \qquad I_p = {wh\over 12}\big(w^2 + h^2 \big) \hskip50pt$$ $$\hbox{circular cross-section of radius $a$} \qquad \Longrightarrow \qquad I_p = {1 \over 2}\pi a^4 \hskip95pt$$
If the bar is free at both ends, this means that there is no torque (moment) at the ends restricting the angular displacement. So, \(\partial \theta / \partial x = 0 \) at both \(x=0\) and \(x=L\). Application of these boundary conditions to a pair of traveling waves in bar: $$ \theta(x,t) = A e^{j(\omega t - k x)} + B e^{j(\omega t + k x)} $$ results in a stand wave of the form $$ \theta(x,t) = \Theta_o \cos(kx)e^{j\omega t}$$ with the allowed wavenumbers and natural frequencies $$k_n = {n\pi \over L} \qquad \hbox{ and } \qquad f_n = {n c_T \over 2L}\; .$$ These are the equations which approximately represent the mode shapes for torsional oscillation of a thin rectangular bar. This simple theory predicts that the frequencies of higher order \(n>1\) torsional modes will be integer multiples of the fundamental \(n=1\). In reality, however, the higher frequencies are not exactly integer multiples.
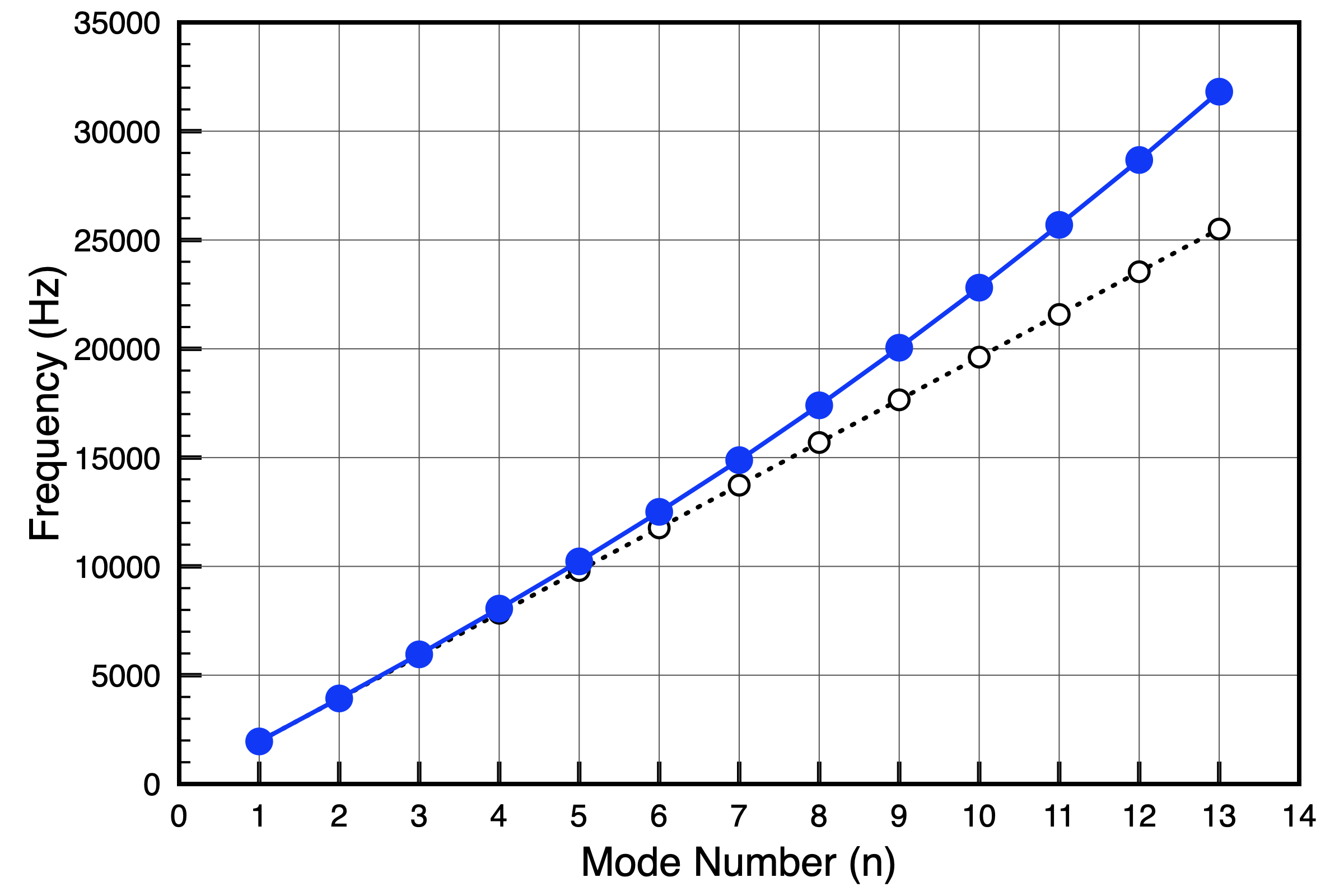
Comparing Realistic and Experimental Frequencies with Simple Theory
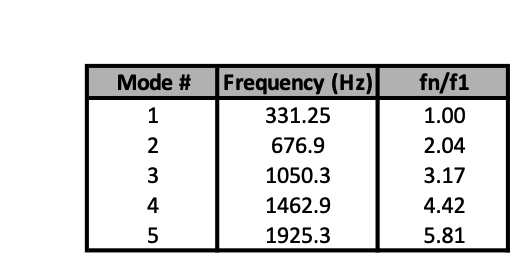
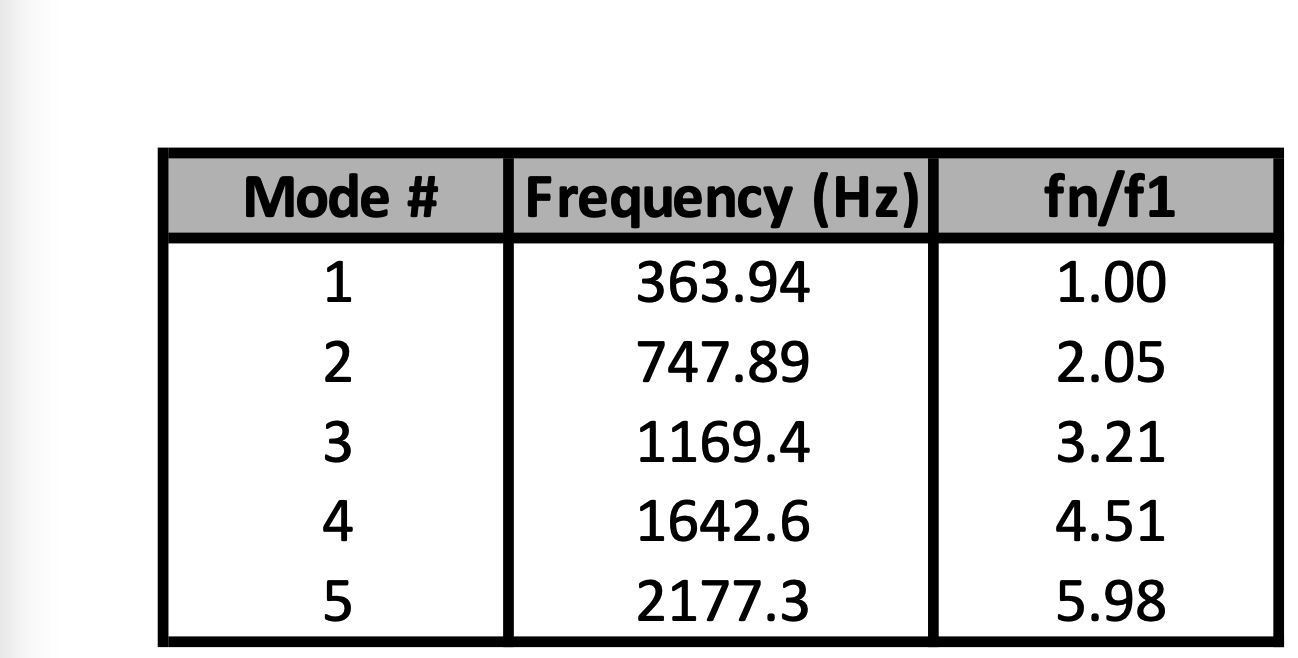
The plot below shows measured frequencies (blue) compared to simple theory for a free-free rectangular bar. Experimentally measured frequencies for larger mode numbers \(n\) become noticeably higher than the simple theory predicts. This is because the simple theory outlined above ignores the effects of warping and the coupling between bending and shear forces. This behavior is also true for a good computational model (like the COMSOL results shown at the top of this page). The table of frequencies at the top of this page shows the frequency ratios for the COMSOL model are all slightly higher than integer multiples of the fundamental, and the disparity increases for higher modes.