Physics and Acoustics of Baseball & Softball Bats
Daniel A. Russell, Ph.D.
Graduate Program in Acoustics
The Pennsylvania State University
The contents of this page are ©2003-2011 Daniel A. Russell
Today is The contents of this page were last modified on September 4, 2008

Swing Weight of a Bat
(Why moment-of-inertia matters more than weight)

Read a preview of my article about swing weight and moment-of-inertia that will be published in The Physics Teacher in October, 2010.

Question: When can a 30oz bat feel lighter than a 28oz bat?        Answer: When you swing it! [1]

In the article I wrote on bat weight and swing speed my discussion required the assumption that the collision between ball and ba took place at the center-of-mass of the bat, and that the rotation of the bat played no role in the problem. This cannot be a realistic analysis, then, since the very act of swinging the bat involves a rotational component of motion. Furthermore, any discussion of the conservation of momentum must also include rotational momentum. Likewise any discussion of the energies involved in the collision must include the rotational kinetic energy of the bat. In this article I'll discuss the rotation of the bat, the rotational inertia of the bat (the distribution of mass compared to the pivot point), and the effect this rotational inertia has on bat swing speed and batted ball velocity.

What is the Difference Between Actual Weight and Swing Weight?

The photo at left shows the knob of a 1997 Dudley Fusion slow-pitch softball bat, one of the only bats I am aware of that advertised a difference between actual weight and swing weight. The knob sticker states that the actual weight of the bat is 23-oz (when I checked it on a precision scale I found its actual weight to be 25.2-oz), but when the bat is swung it definitely feels more like a typical 28-oz bat. So, apparently there is a difference between a bat's actual weight and the perception of weight while the bat is swung.

Here are some examples of extreme differences between weight and swing-weight.

Same actual weight but different swing weight. In my laboratory I have two 30-oz slow-pitch softball bats, one is a 1993 Easton J-Series Graphite model and the other is a 2005 Louisville Slugger Warrior End-loaded. I have weighed both on a precision scale and they are within 0.2-oz of each other. Picking up the bats by the knob and letting them dangle from my fingers, they both weigh the same. However as soon as I start swinging them, the perception that they weigh the same immediately vanishes. The 30-oz Easton Graphite bat swings easily, feeling more like a 26-oz Louisville Slugger Genesis, while the 30-oz Louisville Slugger Warrior feels very heavy when I swing it, feeling more like 34-oz Louisville Slugger Pro II end-loaded or a 38-oz Easton BigMax bottle bat (both from the mid 1980's).

Different actual weight but same swing weight. The opposite behavior can be demonstrated with a 27-oz Miken Ultra and a 30-oz Miken Ultra II. When dangled from my fingers the 30-oz Ultra II definitely feels heavier, as it should since it weighs 3 ounces more. However, when I take practice swings with both bats I can't tell the difference between them. They both feel the same when I swing them.

How is it possible that two bats with the same actual weight feel like they are 8 ounces different when they are swung? How is it that two bats which differ in weight by 3 ounces could feel the same when swung? The answer to both questions has to do with the distribution of mass in each bat. In the language of physics, I'm talking about the moment-of-inertia which depends on both the total weight and the balance point, or center of gravity. In the language of sports equipment I'm talking about swing weight.

The Bat as a Rotating Object

To understand the importance of the rotational properties of a bat and to help illustrate why the swing weight of the bat might be important, let's take a look at the motion of the bat during a typical swing. The movie shown at right was extracted from a longer clip of a college player hitting a slow-pitch softball.[2,3] I should note that in this overhead camera view the swing is reduced to a 2-dimensional motion, in which the bat appears to move in a plane parallel to the ground. This is almost never the case - at the point of impact for most ball-bat collisions (especially in slow-pitch softball), the ball is usually moving downwards while the bat is moving upwards during the swing. However, the overhead viewpoint is sufficient for the purpose of discussing the fundamental aspects of swinging a bat and the primary effects of mass and inertia on the bat swing speed. The overhead view also clearly illustrates that any discussion of how heavy a bat feels while swinging it must include an an analysis of the rotation of the bat during the swing. The key issue is the rotation of the bat, and there are two rotational aspects which come into play. The first is the rotation of the arms and bat together (comprising a single arm-bat system) about a pivot point between the shoulders. The second is the rotation of the bat itself about a pivot point in the wrists

I will freely admit that I am not at all an expert on swing mechanics, and I am aware that the "perfect" swing for fast-pitch baseball is quite different than it would be for slow-pitch softball. However, looking at this movie (and assuming this player is not exhibiting some horrendously bad habits) it would appear that the bat undergoes three distinct phases of motion, and that the relative importance of the rotation about the body ωbody and the rotation about the wrists ωwrists is different for each of the three phases of the swing. [Figure at left adapted from Watts & Bahill.[4]]


Movie clip courtesy of Larry Noble, Kansas State University.
Used with Permission.

[1] Phase 1: Pull-Forward.  The three figures at right are still-frames from the movie showing the motion of the bat during the first part of the swing. The primary component of motion during the first part of the swing is essentially a rotation of the bat-arm system about a pivot point near the player's shoulders. There is, however, no rotation of the bat with respect to the players's wrists. The player's arms and the bat remain at 90o with respect to each other as the bat is pulled around and forward. During this first phase of the swing the actual weight (or mass) of the bat is more important since the player must overcome the inertia of the bat to begin moving from rest, but the bat does not change its orientation to the player as it moves. Differences in actual bat weight would be noticeable to a player during this portion of the swing, but differences in the balance point would probably not matter much because the bat is not rotating with respect to the player's hands or wrists.

[2] Phase 2: Wrist Rotation.  During the second part of the swing the bat undergoes both types of rotation. There is a small amount of rotation of the bat-arm system about a pivot point near the shoulders. However, the more important motion is a rotation of the bat about a point that appears to be centered near the player's wrists. The player's arms do not move very much during this part of the swing. Instead the player's wrists create a torque which rotates the bat through 90o until it makes contact with the ball. The bat rotates from being essentially parallel to the ball's path to being perpendicular to the ball's path at the moment of impact. During this part of the swing, when the bat is primarily rotating about a point near the player's wrists, the actual weight of the bat is less important than the swing weight (moment-of-inertia). During this phase of the swing, two bats with the same actual weight but different swing weights would be easily distinguished. The bat with the lighter swing weight will be easier to control and easier to generate a quick whip action to achieve greater bat speed just prior to the collision with the ball. Or, if the bat is end-loaded the larger rotational inertia of the bat will make it more difficult for a player to check his/her swing. This "wrist-rotation" phase of the swing is what generates the maximum bat speed just prior to collision with the ball.

[3] Phase 3: Follow Through.  The final phase of the swing consists of the follow through. The ball-bat collision is over but the bat is still moving. As was the case for the first part of the swing, the angle between the bat and the arms stays pretty much constant and the arm-bat system simply rotates about a pivot point near the shoulders.

Swing Weight, the Balance Point, and the Moment-of-Inertia

So, what is it about a bat that would make it easier to rotate about the wrists in order to generate higher bat speed? Let's look closer at two of the slow-pitch softball bats that I mentioned earlier from my research laboratory. The top bat in the photo at right is a 30-oz 1993 Easton J-Series Graphite bat and the bottom bat is a 30-oz 2005 Louisville Slugger TPS Warrior end-loaded, aluminum bat. The difference between the two bats is the way that the 30-oz is distributed along the bat length. The balance points (indicated by the yellow lines in the photo) are more than 4-inches apart, with the balance point of the Easton graphite bat being closer to the handle than that of the Louisville Slugger aluminum bat. Moving the balance point closer to the handle causes the bat to have a much lower swing weight, and the bat feels much lighter and is much easier to swing.

It might be tempting to just use the weight and the balance point of the bat to specify the swing weight. I have seen a couple of websites that attempt to share swing weights for a large number of bats, but they all incorrectly calculate "swing weight" values by simply multiplying the measured balance point by the measured weight. In reality, swing weight is a little more complicated. While the balance point (center-of-gravity) of an object is a single fixed location, the rotational inertia (opposition to a change in rotational motion) depends on the location of the pivot point about which the object rotates. It is this moment-of-inertia of the bat, not just the balance point, that determines bat-swing speed and the effectiveness of the collision between bat and ball.

The moment-of-inertia (MOI) of an object depends on the mass of the object and how that mass is distributed with respect to the pivot point. It is true that placing mass further from the pivot point increases the MOI. However, while the weight and balance point are related to MOI, calculating the MOI for a bat is more complicated than simply multiplying the two. (I've got a separate page that discusses the details of how MOI depends on mass distribution, but it involves more mathematics than is necessary here.) Instead, it might be more meaningful to discuss how MOI is measured by the bat industry.

The industry standard laboratory tests[5] which are currently used to regulate bat performance require the moment-of-inertia of a softball or baseball bat to be measured with reference to a pivot point on the handle, 6-inches from the knob end of the bat.[6] The bat is gripped at the 6-inch point in a pivot support that allows the bat to swing back and forth like a pendulum. The period (time for one complete pendulum swing) is measured carefully with an infrared triggered timing mechanism. Knowing the period T, the mass m, the acceleration due to gravity g, and the distance d between the pivot point and the balance point, you can calculate the moment-of-inertia from


The table at left shows the weight, balance point (measured from the end of the knob) and moment-of-inertia (about the 6-inch point on the handle) for the 1993 Easton J-Series Graphite and 2005 Louisville Slugger TPS Warrior bats that feel so different when swung. The shift of the balance point closer to the handle causes the graphite bat to have a much lower moment-of-inertia. The differences in the moment-of-inertia between the two bats are huge and this clearly identifies why the two bats feel so different when they are swung.

  

Why is the MOI measured with respect to the 6-inch point on the handle?

Much of the early research on baseball bats assumed that the pivot point during the entire swing, including the rotation just prior to impact, was located under the top hand about 6-inches from the knob of the handle.[7] However, recent field studies have shown that for both softball[8] and baseball[9] the actual pivot point of the bat (the instantaneous center of rotation) during impact with the ball is about 2.5 inches beyond the knob and about 1.5 inches off the long axis of the bat. A sampling of data points from a recent field study of top amateur slow-pitch softball players is shown at right.

Ultimately in our discussion of swing speed and bat properties, the exact location of the pivot point doesn't matter so much as long as we pick one pivot location and use it for all of our comparisons. In fact, if you know the weight, balance point location and the moment-of-inertia about a specific pivot location, you can calculate the moment-of-inertia about any other pivot point location. In the performance standard used to certify softball bats for the Amateur Softball Association, the MOI is measured at the 6-inch point on the handle, but the bat-swing speed is calculated using the MOI about a pivot point 2-inches beyond the end of the handle, in accordance with the measured field study data.


Graphic courtesy of Lloyd Smith, Washington State University Sport Sciences Laboratory.[6] Used with Permission

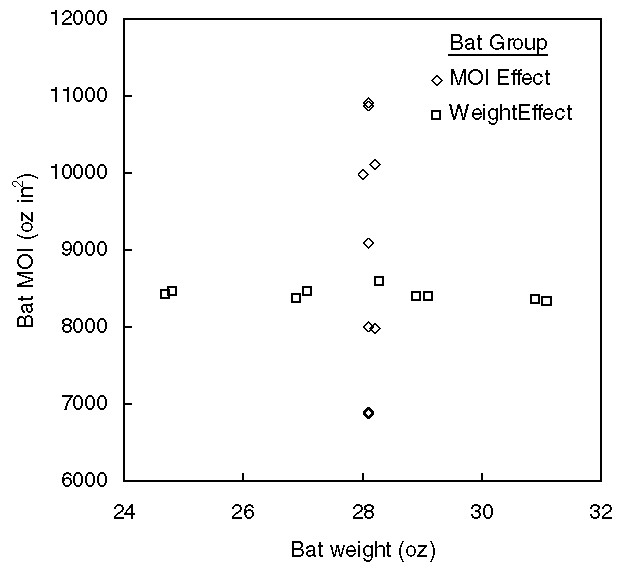
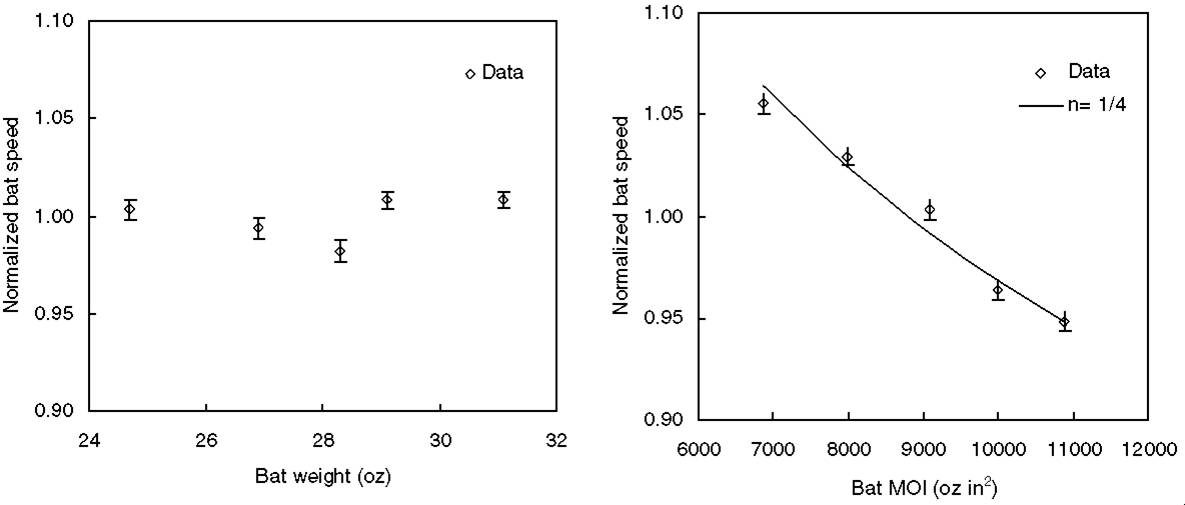
What effect does MOI have on bat performance?

Moment-of-Inertia and Bat Swing Speed

So, how does the rotation of the bat affect the speed with which the bat is swung? Well, put simply, the larger the MOI of the bat the more difficult it is to swing the bat quickly. A lower MOI bat may be swung with greater speed and greater control. Several recent field studies of real players swinging both softball bats[8,10] and baseball bats[9,11-13] have conclusively demonstrated that the speed with which a player can swing a bat depends very strongly on the moment-of-inertia of the bat.

An example of one data set (for slow-pitch softball[14]) is shown below. A selection of top level players were filmed with high-speed cameras while they were swinging two sets of bats (left graph below). The first set of bats had the same total weight, but the weight was distributed differently so that the bats had different moments-of-inertia. The second set of bats had the same moment-of-inertia, but different total weights. The speed of the bat, just prior to impact with the ball, was measured and the data was normalized for each player. The results clearly show (middle graph below) that when the moment-of-inertia was kept the same, the bat-swing speed did not vary as the total weight of the bat changed. In contrast, the bat-swing speed for all players was noticeably slower for larger MOI bats than for smaller MOI bats with the same total weight (right graph below).


This data suggests that while the first phase of the swing - the "pull-forward" phase - might be affected by the bat weight, the rotation of the bat about the hands just prior to impact with the ball depends on the moment-of-inertia. A bat with lower moment-of-inertia may be swung faster, even if the actual weight of the bat is larger.

Bat Swing Speed and Batted-Ball Speed

Bat-swing speed is important because (assuming everything else remains the same) the faster the bat speed, the faster the resulting batted-ball speed. The speed with which a batted ball leaves the bat (the Batted-Ball Speed, or BBS) depends on three things: the pitched-ball speed vball, the bat-swing speed vbat, and the efficiency of the collision between bat and ball, eA according to:
BBS = vball eA + (1 + eA) vbat
This equation states that if a player can increase his/her bat-swing speed (while using the same bat) the resulting batted-ball speed will increase proportionally. The graph at right shows experimental field data[13] for a number of baseball players swinging the same wood bat. The horizontal axis marked "Impact Speed" represents the speed of the bat just prior to impact with the ball. The dotted line in the graph shows that a 10-mph increase in bat-swing speed produces a 10-mph increase in batted-ball speed. Note, however, that this increase in BBS results from an increase in bat-swing speed for the same bat. Swinging a given bat faster will result in a faster batted-ball speed. However, swinging a lower MOI bat with a faster swing speed will not increase the batted-ball speed.

Trade-off between higher bat speed and less effective collision

Before you run out to purchase a new bat with lowest moment-of-inertia you can find in order to increase your bat-swing speed in hopes of hitting balls faster, there is a catch. It is true that lower MOI translates to higher bat-swing speed, and that higher bat-swing speed results in higher batted-ball speed. However, a gain in batted-ball speed only results if you are swinging the same bat faster. Swinging a lower MOI bat faster does not resulting in a faster batted-ball speed. This is because the effectiveness of the collision between bat and ball depends on the MOI of the bat, and a lower MOI bat produces a less effective collision with the ball. If the bat-swing speed is held constant, a bat with a lower moment-of-inertia produces a less-effective collision with the ball such that the batted-ball speed actually decreases for the lower MOI bat. In fact, when a player switches to a lower MOI bat, the increase in batted-ball speed due to higher swing speed is almost exactly cancelled out by the reduction in batted-ball speed because the lower MOI bat impacts the ball less effectively. I discuss this trade-off between higher bat-swing speed and lower collision efficiency in my article on the BESR and MOI performance standard for NCAA baseball bats. The trade-off between bat-swing speed and collision efficiency due to changes in moment-of-inertia is also the reason that corking a bat may help a player increase his batting average, but will not enable him to hit more home runs.

If a lower MOI bat doesn't hit balls as effectively, why would a player want to switch to a lower MOI bat? A lower MOI bat would provide a player with greater bat control. The increase in bat-swing speed means a player could wait a split second longer before committing to a swing. Waiting a couple of milliseconds would allow a player to watch a fast-pitched baseball travel an additional 5-6 feet before having to commit to a swing - and that additional time (distance) could enable the player to distinguish between a curve or sinker, or between a strike or ball. Bat control would improve for a lower MOI bat, and that might allow a player to make solid contact with the ball more frequently. But, a lower MOI bat will not help a player hit balls faster. So, if you want to increase your batting average, switch to a lower MOI bat. But, if you want to hit more home runs (which requires a faster BBS) you'll need to increase your arm and upper body strength and generate a faster bat-swing speed.

Why Don't Bat Manufacturers List Swing Weight?

This is one of those 64-million dollar questions, and unfortunately not knowing the MOI values of a group of bats makes it difficult to apply much of the information in this article. If you go looking for a new tennis racket or a set of golf clubs you'll either find a swing weight number not stamped on the racket or club, or you'll be able to easily obtain that information from the supplier or manufacturer. However, the only thing you will find on a baseball or softball bat is the actual weight. Manufacturers - so far - have chosen not to share MOI values for bats with the public. Manufacturers measure the MOI of every single bat model (and they design bats to have a certain MOI). And, governing bodies either regulate the MOI values of bats (as the NCAA does for college and high school baseball bats) or they account for the MOI and its effect on bat-swing speed when regulating performance (as the ASA does for their 98-mph slow-pitch softball performance standard). Unfortunately, MOI values of bats are not shared with the public who purchase and swing the bats. A player is left with the possibly frustrating experience that not all 28-oz softball bats feel the same when swung, and that new $300 bat you just bought might not feel right when you swing it.

As of Summer 2008, the only bat manufacturer I am aware of that comes close to listing MOI values for their bats is CE-Composites, makers of the Combat® line of baseball and softball bats. CE-Composites lists the actual weight of the bat along with a proprietary "swing weight number" that is related to the moment-of-inertia of the bat and its balance point (center-of-mass). A player can obtain bats in just about any combination of actual and swing weights. Thus, a player who prefers a lighter actual weight for the first "pull-foward" phase of the swing, but wants a heavier swing weight during the second "wrist torque" rotation phase of the swing just prior to contact can find a bat that exactly suits his/her needs. Perhaps in the next couple of years other manufacturers will start following suit and listing swing weights as well as actual weights for softball and baseball bats. My preference would be for manufacturers to provide the MOI value along with the weight.

References

[1] I borrowed this question and answer from an article (reprinted from the April 2002 issue of Tennis Magazine) posted on the Tennis Company website.
[2] Larry K. Noble, "Elastic and Rigid Body Properties of Bats," Mini-symposium presentation at the Annual Meeting of the American College of Sports Medicine, Baltimore, MD, May 30-June 3 (2001).
[3] L. Noble and D. Zollman, Physics of Sport Videodisk,(Videodiscovery Inc., 1988) *Permission to reproduce the movie clip here was obtained from Larry Noble.
[4] R. G. Watts and A. T. Bahill, Keep Your Eye On The Ball: Curve Balls, Knuckleballs, and Fallacies of Baseball, (W.H. Freeman, New York, 2000).
[5] ASTM F1881-04 Standard Test Method for Measuring Baseball Bat Performance Factor; ASTM F1890-04 Standard Test Method for Measuring Softball Bat Performance Factor; ASTM F2219-04 Standard Test Methods for Measuring High Speed Bat Performance
[6] ASTM F2398-04e1 Standard Test Method for Measuring Moment of Inertia and Center of Percussion of Baseball of Softball Bats,
[7] L. Noble and X. Eck, "Emperical determination of the axis of percussion of softball and baseball bats," in Biomechanics IX-B, D.A. Winter, R.W. Norman, R.P. Wells, K.C. Hayes, and E. Patla (Eds.), Champaign, IL (1985) pp. 516-520.
[8] Smith, L, Broker, J, Nathan, A, “A Study of Softball Player Swing Speed,” Sports Dynamics Discovery and Application, Edited by A. Subic, P. Trivailo, and F. Alam, RMIT University, Melbourne Australia, pp. 12-17 (2003)
[9] J.J. Crisco, R.M. Greenwald, L.H. Penna, and K.R. Saul, "On Measuring the Performance of Wood Baseball Bats," in The Engineering of Sport, A.J. Subic and S.J. Haake (Eds.), pp. 193-200 (Blackwell Science, 2000)
[10] K. Koenig, N. Mitchel, T. Hannigan, and J. Clutter, "The influence of moment of inertia on baseball/softball bat swing speed," Sports Engineering, 7(2), 105-118 (2004).
[11] G. Fleisig, N. Zheng, D. Stodden, and J. Andrews, "Relationship between bat mass properties and bat velocity," Sports Engineering, 5(1), 1-8 (2002).
[12] J. Clutter and K. Koenig, "The effect of baseball bat properties on swing speed," Proceedings of the 4th meeting of the American Society of Mechanical Engineers, Bioengineering Division, Edited by V. Goel, R. Spilker, G. Atheshian, and L. Soslowsky, pp. 629-630 (Big Sky MT, June 1999)
[13] J.J. Crisco, R.M. Greenwald, J.D. Blume, and L.H. Penna, "Batting performance of wood and metal bats," Med. Sci. Sports Exerc., 34(10), 1675-1684 (2002)
[14] L.V. Smith, unpublished data from a slow-pitch field study at Montgomery, AL (2002)
Back to Physics and Acoustics of Baseball & Softball Bats