Physics and Acoustics of Baseball & Softball Bats Daniel A. Russell, Ph.D. Applied Physics, Kettering University, Flint, MI 48504-4898 The contents of this page are ©2008 Daniel A. Russell

Inertia is a measure of how difficult it is to change the velocity of an object by applying a force, and is usually expressed in terms of mass. The greater the inertia of an object (i.e., the more mass an object has), the more difficult it is to change its velocity. Mass is different from weight though the two terms are often used interchangeably. [Since I am a physics professor I feel obligated to explain the difference between the two before moving on to discuss baseball and softball bats. Mass is a property of an object; a given object will have the same mass regardless of where in the universe it happens to be located. A bowling ball has the exactly same mass on earth as it does on the moon, or somewhere out in space where it is free from the pull of gravity. Trying to stop a moving bowling ball in space is just as difficult as it is on earth. Weight is a force, specifically the force that an object experiences when placed in a gravitational field. The strength of the gravitational field depends on the mass of the object creating the field as well as on the square of the distance from that object. The gravitational field of the moon is only about 1/6 that of the earth. So, while a bowling ball has the same mass on earth as it does on the moon (and thus its velocity would be just as difficult to change in both locations) the weight of the ball on the moon would be 1/6 of its weight on earth.]
Rotational inertia, or the moment-of-inertia (MOI) is a measure of how difficult it is to change the rotational velocity of an object which is rotating about a pivot point. The larger the moment-of-inertia, the more difficult it is to change the rotational speed of the object. The value of the MOI depends on the total mass of the object as well as the way in which that mass is distributed about the pivot point. Consider first a point mass m (a small ball) which is rotating parallel to the ground at a distance x from a fixed pivot point, as is shown in the image at top right. The MOI of the point mass is the product of the mass and the square of the distance from the pivot point:	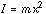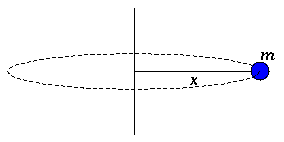Single point mass rotating at a fixed distance from a pivot point.
If there are several point objects all rotating about the same pivot point, but at different distances from the pivot, then the total moment-of-inertia of the system is just the sum of the individual moments-of-inertia.	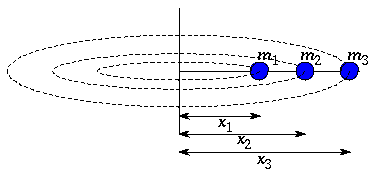Multiple point masses rotating at a various distances from a pivot point.
In our case the object which is rotating is a bat, with mass distributed along its entire length. In order to solve this more difficult problem, we pretend that the bat is made up of very large number of very small slices, each with its own incremental mass dm and each being located at a distance x from the pivot point. If we knew how the mass dm varied with position we could add all the individual moments-of-inertia together to obtain the total inertia of the bat. 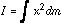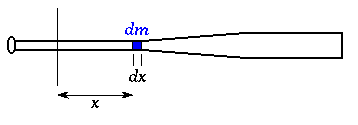However, very few people actually have the mass distribution function dm for a given baseball or softball bat at their fingertips, so calculating the moment-of-inertia for a bat isn't very practical. It turns out that the moment-of-inertia is much easier to measure than it is to calculate, so I won't attempt to explain how we would solve for the inertia, but instead will describe how it is measured and what it means.	Extended object (bat) pivoting about a fixed axis may be broken up into many small pieces with varying mass and varying distance from the pivot point.

Weight and Balance Point To measure the weight of the bat you could just put it on a scale and record the weight directly. To find the balance point, you could use a knife edge and find the location where the bat exactly balances. This is a bit tricky but it works pretty well. Or you could follow the procedure for measuring weight and balance point as spelled out in ASTM Standard F2398-04 "Test Method for Measuring Moment of Inertia and Center of Percussion of a Baseball of Softball Bat" which is what bat manufacturers and governing associations do. This test standard requires the use of two scales, one which supports the bat at a point 6-inches from the end of the knob, and the other which supports the barrel of the bat at a distance of 24-inches from the knob. The weight of the bat is just the sum of the two scale readings W = W6 + W24 and the balance point is calculated from BP = (6*W6 + 24*W24) / (W6 + W24)

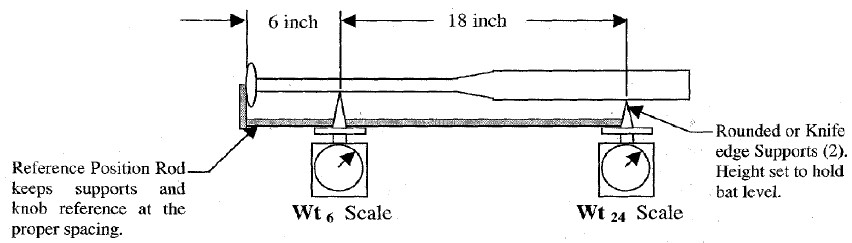
Knowing the location of the balance point is important. The moment-of-inertia is always calculated or measured with respect to a specified pivot point. According to the standard practice[1] used by manufacturers, test labs and governing bodies, the pivot point is taken to be on the handle 6-inches from the knob end of the bat. In laboratory tests to measure bat performance, the bat is gripped at the 6-inch point on the handle, so the moment-of-inertia about this location is relevant to the tests. However, several field studies of bat-swing speed have used the moment-of-inertia of the bat with respect to a pivot point at the knob. The MOI values for the two pivot points are quite different. However, it is possible to convert from one to the other as long as you know one of the MOI values and the pivot location, the weight of the bat, and the location of the balance point (center-of-mass). The parallel axis theorem states that the moment-of-inertia about an axis through the center-of-mass (Icm) and the moment-of-inertia about a different axis which is parallel to the axis through the center-of-mass are related by: 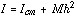where M is the total mass of the object and h is the distance between the actual axis of rotation and the center-of-mass. So, if you measure the MOI for a pivot point 6" from the end of the knob, you can use the parallel axis theorem to calculate Icm. Then you can use the value of Icm and the parallel axis theorem again to calculate the moment-of-inertia about some other axis (say, about the knob).	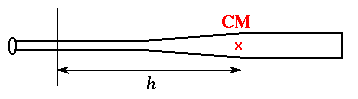Center of Mass or Balance Point.
One additional quantity that is often mentioned along with moment-of-inertia is the radius of gyration. The radius of gyration is the distance R from the pivot point where a point mass (small ball) with the same mass as the total mass M of the bat would be located, so that the moment-of-inertia of this point mass ball would be the same as the moment-of-inertia of the actual bat.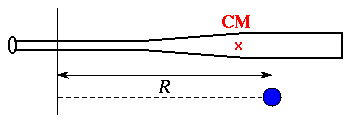I = M R2	Radius of Gyration compared to the Balance Point.

Measuring the Moment-of-Inertia of a Baseball of Softball Bat

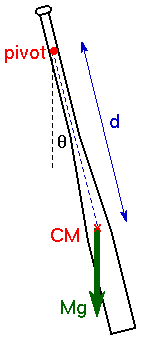
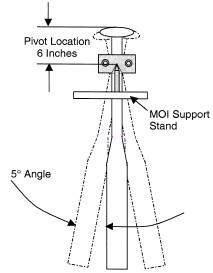
The industry standard laboratory tests, currently used to regulate bat performance, require the moment-of-inertia of a softball or baseball bat to be measured with reference to a pivot point on the handle, 6-inches from the knob end of the bat. The bat is gripped at the 6-inch point in a pivot support that allows the bat to swing back and forth like a pendulum. The period (time for one complete pendulum swing) is measured carefully with an infrared triggered timing mechanism. Knowing the period T, the mass m, the acceleration due to gravity g, and the distance d between the pivot point and the balance point, the moment-of-inertia is then calculated from

References