|
Physics and Acoustics of Baseball & Softball Bats
Daniel A. Russell, Ph.D. Graduate Program in Acoustics The Pennsylvania State University The contents of this page are ©2003-2011 Daniel A. Russell | 
|
|
|
Physics and Acoustics of Baseball & Softball Bats
Daniel A. Russell, Ph.D. Graduate Program in Acoustics The Pennsylvania State University The contents of this page are ©2003-2011 Daniel A. Russell |
|
| NOTE (3/27/08): This article is a summary of the published literature concerning batted-ball speed and bat WEIGHT. However, a great deal of recent research clearly indicates that the distribution of weight (as measured by the moment-of-inertia) is far more important than the weight itself. As a result, some of the conclusions summarized below are no longer entirely realistic. I am currently writing an article summarizing the influence of moment-of-inertia (MOI) on bat swing speed and batted-ball speed. |
|  Some of the Little League bats I have tested in Kettering University's Acoustics Laboratory. Bats in photo do not exactly match list in table. |
|
The answer to that question is "both," though past players tend to have used heavier bats than do today's players.
Baseball's "king of swat" Babe Ruth reportedly began his hitting career using a 54 ounce (1.5 kg) hickory bat, and is known to have used a 40oz bat in 1927 when he hit his 60 home runs.[1] Ty Cobb and Joe Di Maggio both played with 42oz bats and Rogers Hornsby used a 50oz piece of lumber. George Sisler, playing for the St. Louis Browns in the 1920's, made his bat heavier by hammering Victrola needles into the barrel of his bat.[2] In the 1950's Cincinnati Reds' Ted Kluszeski hammered tenpenny nails into his bat to make it heavier.
Other great hitters including Ted Williams, Rod Carew and Stan Musial used much lighter bats: 31-33oz.[1] Roger Maris used a 33oz bat to hit his 61 home runs in 1961. Many players have tried to make their bats lighter by drilling a hole in the barrel and filling it with cork. Detroit Tigers' Norm Cash admitted to using a corked bat in 1961 when he won the batting title with a .361 average (though he slumped to .243 the next year with the same corked bat).[2] Kirkpatrick[3] reports that Roger Maris participated in a 1962 experiment in which he batted for distance with 5 different new bats whose weights varied from 33 to 47oz. He hit 5 long fly balls with each bat and the distances were measured and correlated to bat weight. The heavier bats, on average, resulted in further distance. However, Maris' preferred bat (which he used to break Babe Ruth's home run record) was the lightest of the set, even though it produced the shortest distance fly balls. Mark McGwire used a 35oz bat to hit his 70 home runs in 1998, and Barry Bonds used a 32oz bat to hit his 73 home runs in 2001. Most of today's major league players typically use 31-35oz bats. Physicists have shown,[3,4] from a simple collision analysis, that the optimum bat weight is between 15 and 18oz. However, no professional batter uses a bat this light (in fact, you cannot make a wood bat this light). NCAA regulations[x] recently imposed a -3 rule (length in inches minus weigh in ounces cannot exceed 3) so that 34 inch bats must weigh 31oz. So far no such rule exists for Little League play, and -12 composite bats were introduced for the 2003 season. This brings us back to our original questions: which is better: heavier or lighter bats? So, what is the optimum bat weight, and what criteria influence this choice? Let's start by looking at the collision between ball and bat. |
 Ty Cobb and his 42oz bat |
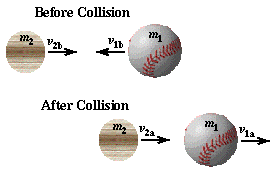The impact between bat and ball is a collision between two objects, and in its simplest analysis the collision may be taken to occur in one-dimension. In reality most collisions between bat and ball (especially the ones I am able to make) are glancing collisions which require a two-dimensional analysis. It turns out, in fact, that a glancing blow is necessary to impart spin to the ball which allows it to travel farther.[5] Maybe I'll write about this more interesting, but more difficult problem later, but for right now I'll keep things simple and look at the collision in one-dimension only. The ball, m1, and bat, m2, both have initial velocities before the collision (subscript "b"), with the ball's velocity being negative. After the collision (subscript "a") both bat and ball have positive velocities. The before and after velocities and the masses of bat and ball may be related to each other through the physical relationship known as the conservation of linear momentum. Linear momentum is the product of the mass and velocity of an object, p=mv. If the net force acting on a system of objects is zero then the total momentum of the system is constant. While the bat and ball are in contact the player is exerting a force on the bat; the force needed to swing the bat. So, in a completely correct analysis, momentum is not constant because of this force exerted by the player swinging the bat. However, the force on the bat by the player is very much smaller than the forces between bat and ball during the collision, and the contact time between ball and bat is very short (less than 1 millisecond). This allows us to ignore the force on the bat by the player during the collision between ball and bat without significantly affecting our results. If we ignore the force by the player on the bat, we can express the conservation of linear momentum by setting the total momentum before the collision equal to the total momentum after the collision.
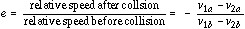
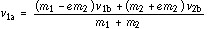
This equation tells us how the batted ball velocity (v1a)depends on the mass of the ball (m1) and bat (m2), the elasticity of the ball (e), the pitched ball speed (v1b) and the bat swing speed (v2b). The properties of the ball may be treated as constants since they don't change during a turn at bat. The hitter has no control over the pitched ball speed, and while it may vary considerably from pitch to pitch we'll assume that it is a constant. The only two remaining variables which determine the final velocity of the ball are the mass of the bat, m2 and the initial speed of the bat, v2b. If we know these two parameters, we can predict the batted ball speed. As we will see, however, the problem is complicated somewhat by the fact that the speed with which a player can swing a bat depends on the weight of the bat.
|
To see the effects of bat weight and bat speed, here is a summary of an experiment that I found summarized in a 1980 high-school textbook, Physics of Sports developed by Florida State University.[6] For this experiment, the ball mass, pitch speed, and bat swing speed were all kept constant. Only the bat mass was changed. The data shows that a heavier bat produces a faster batted ball speed. This makes intuitive sense since a heavier bat brings more momentum into the collision. Doubling the mass of the bat results in an increase of almost 12mph. So, using a heavier bat should result in faster hit balls, which means the hit ball will travel farther. If a player can maintain the same bat swing speed with a heavier bat, the heavier bat will produce higher batted ball velocity and an increase in distance.
But, any player who has experimented swinging bats with widely different weights knows that it is easier to swing a light bat than a heavier bat. Put another way, it takes more effort to swing a heavy bat with the same speed as it does a lighter bat, and most players cannot swing a heavy bat as quickly as they can a bat which is half the weight. So, we need to see how the batted ball speed depends on bat swing speed. |
|
|
A similar experiment (from the same 1980 high-school textbook Physics of Sports developed by Florida State University[6]) changed the bat swing speed while the the ball mass, pitch speed, and bat mass (30oz) were all kept constant. The data shows that a faster bat swing produces a faster batted ball speed. Doubling the swing speed of the bat results in an increase of almost 22mph. So, it would seem that swinging the same bat faster is more beneficial than swinging a heavier bat at a the same speed. Ideally, the best result would be to swing a heavier bat faster. But, as I already stated, it is harder to swing a heavier bat with the same speed, let alone swing a heavier bat faster.
So, it looks like we have two different effects (increasing bat weight and increasing bat swing speed) which both result in faster batted ball speeds. However, it does not seem possible to get both effects at the same time. In fact, increasing bat weight might decrease bat swing speed. So, we need to see how these two parameters are related before we can answer the question "what is the final batted ball speed?" |
|
Let's assume that the mass of the baseball is a constant m1=5.125oz, the coefficient of restitution is e=0.55, and that the initial velocity of the baseball is representative of a typical pitch speed, (v1b=-90mph for the Major League player and v1b=-40mph for the Little League player). Then we can substitute either of the equations for bat speed into the equation for batted ball speed and make some plots like those shown by Bahill in his papers[2,7] and book[8]. The blue dots with error bars represent measurements of bat swing speed for various bat weights. The blue curve in each plot shows how the bat swing speed decreases with increasing bat weight according to the equations above. The red curve in each plot shows how the resulting batted ball velocity depends on both the bat weight and the bat swing speed. Notice that the curves are very different for the Major League power hitter and the Little League. The professional has much more control over his bat swing speed, and can produce much greater final ball speed.
 
|
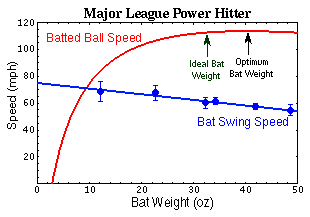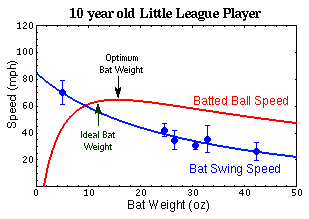
Perhaps a pertinent question is why a major league power hitter would choose to use a lighter bat (say 32oz) when an optimal 41oz bat would produce a higher batted ball velocity? Two possibilities come to mind. First, the fact that you can swing a lighter bat faster means that you can wait just a little bit longer before committing to a swing. For a professional, the ability to wait even 1/10th of a second longer to watch a pitched ball can result in a considerable improvement in the chance of making contact. Secondly, most hitters can control a lighter bat more effectively than they can a heavier bat. Bat control affects the location of the bat as it crosses the plate, and more control over bat location is definitely a good thing when the pitched ball crosses the plate considerable variation in height or distance from the batter. Notice further, from the plot for the major league power hitter, that for bat weights in the range of 35oz to 45oz there is very minor change in the batted ball velocity. Using a 33oz bat instead of a 41oz bat will only very slightly reduce the batted ball velocity, but it will have a significant affect on the bat swing speed and the resulting swing time. Based on such a trade-off between ball speed and bat control, Bahill has defined the Ideal Bat WeightTM as the weight at which the batted ball speed drops 1% below the speed of the optimum batted ball speed bat weight. As shown in the plot, the Ideal Bat Weight for the power hitter is about 32-33oz. This is right in the weight range used by most professional players.
The results for the Little League player are quite different. The optimum bat weight, for maximum batted ball speed, is about 16oz, and the Ideal Bat Weight is about 12-13oz. As was shown in the table at the top of this page, most available 30-inch wood and aluminum Little League bats weigh between 20 and 26oz, which is well above both the optimum and ideal weights for this player. From the plot we can see that if this player used a 23oz bat he would have a much lower bat swing speed and a significantly lower batted ball velocity. Most young players are forced to use bats which are heavier than the ideal bat weight because light enough bats are not available. Only this year (2003) have composite bats become available that begin to approach 16oz for a 30-inch bat.
| Player | Recommended Bat Weight (oz) |
|---|---|
| Major League Baseball | Height/3 + 7 |
| Amateur Baseball | Height/3 + 6 |
| Fast Pitch Softball | Height/7 + 20 |
| Slow Pitch Softball | Weight/115 + 24 |
| Junior League Baseball (13-17 yrs) | Height/3 + 1 |
| Little League Baseball (11-12 yrs) | Weight/18 + 16 |
| Little League Baseball (9-10 yrs) | Height/3 + 4 |
| Little League Baseball (7-8 yrs) | Age*2 + 4 |
References
[1] S. Ashley, "Getting Good Wood (or Aluminum) on the Ball," Mechanical Engineering, 112(10), 40-47 (1990)
[2] Terry Bahill and William Karnavas, "The ideal baseball bat," New Scientist, 130, 26-31 (April 6, 1991)
[3] P. Kirkpatrick, "Batting the ball," American Journal of Physics, 31(8), 606-613 (1963)
[4] P. Brancazio, Sport Science: Physical Laws and Optimum Performance, (Simon and Schuster, 1984)
[5] Robert G. Watts and Steven Baroni, "Baseball-bat collisions and the resulting trajectories of spinning balls," American Journal of Physics, 57(1), 40-45 (1989)
[6] Physics of Sport, (Ginn and Company, 1980), part of the Individualized Science Instructional System for Grades 9-12, developed by Florida State University.
[7] A. Terry Bahill and Miguel Morna Freitas, "Two Methods for Recommending Bat Weights," Annals of Biomedical Engineering, 23(4), 436-444 (1995)
[8] Robert G. Watts and A. Terry Bahill, Keep Your Eye on the Ball: Curve Balls, Knuckleballs, and Fallacies of Baseball, revised ed. (W. H. Freeman and Co., 2000)