Acoustics and Vibration Animations
Daniel A. Russell
Graduate Program in Acoustics, The Pennsylvania State University

An Interactive Waveguide Animation

The animation below shows video clip of a Mathematica Computational Document Format (CDF) animation of a logitudinal wave in a duct being driven at the left end (the source is the red "piston"). The interactive animation may be downloaded as a (Computational Document Format (CDF file) and played by downloading the Free CDF Player from Wolfram.com.

Once you have downloaded the CDF file and the free CDF player, you can change the driving frequency of the source, and you can change the mode number of the wave shape that the piston is attempting to excite. When the driving frequency is above the cut-on frequency for that mode, the modeshape will begin to propagate to the right, down the duct.

How to use the Interactive Animation

• Frequency Slider -- Moving the frequency slider will change the excitation frequency. Clicking on the [+] to the right of the slider will allow you to see the value of the normalized frequency. You can then use the + or - buttons to incrementally change the frequency value.
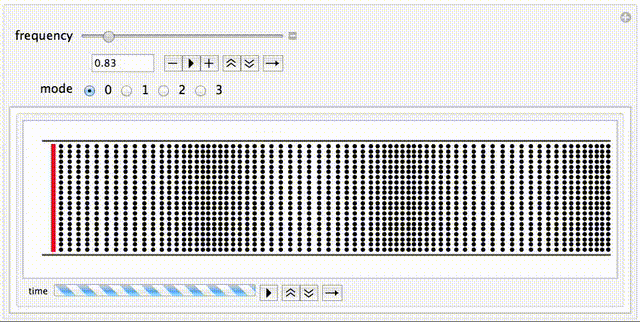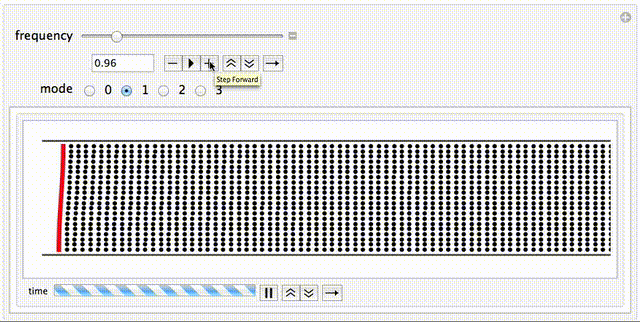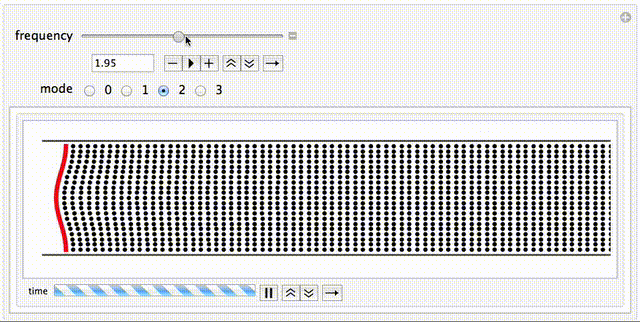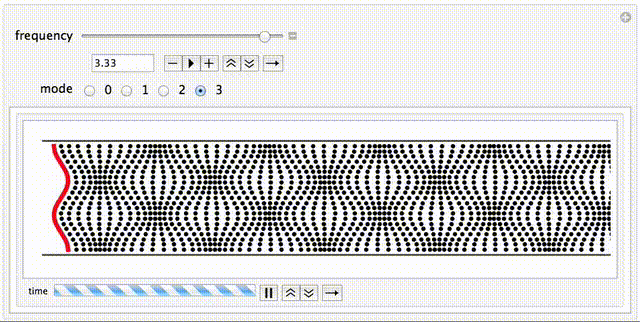
• Mode Number -- use these radio buttons to select the mode you want to try to propagate down the duct. n=0 is the plane wave, and n=1,2,3 are higher modes. This animation has been setup so that the cut-on frequency for each mode is equal to its mode number. Higher modes will be evanescent (exponential decay without propagation) unless the excitation frequency is greater than the cut-on frequency.
• Play / Pause -- you can pause the animation by clicking on the pause/play button under the animation.

Some Observations to Make

• Plane Waves -- For a rigid-walled duct, a plane wave (the n=0 mode) has a cut-on frequency of 0 Hz, which means that the plane wave will always propagate for every excitation frequency. Also, the phase speed for plane waves is constant, and equal to the speed of sound in the medium. If you track the time for plane wavefront (compressed region) to travel down the duct, you should find that will be the same for low and high frequencies. The wavelength will shorten as the frequency increases, the the speed will remain constant.
• Evanescent Modes -- for higher modes (n=1,2,3) the wave will only propagate down the waveguide if the excitation frequency is larger than the cut-on frequency. For this example, the frequency has been normalized so that the cut-on frequency is the same as the mode number; for the n=1 mode, propagation occurs when frequency is greater than 1. If the frequency is less than the cut-on frequency, the wave is evanescent and will not propagate. You can explore this by starting with the n=1 mode and a frequency of 0.81, so that this mode is not propagating even though it is being driven with large amplitude. As you increase the frequency to 1.81 you will see the n=1 mode begin to propagate. Then with the frequency af 1.82, change to the n=2 mode, and you will notice that this new mode is evanescent until the frequency is increased above 2. What happens to the n=3 mode for frequencies below and above 3?
• Phase Speed -- For non-plane modes (n=1,2,3) the apparent speed of the wave (observed by tracking a wavefront as it moves down the duct) may be seen to decrease as the frequency increases.