Acoustics and Vibration Animations
Daniel A. Russell
Graduate Program in Acoustics, The Pennsylvania State University

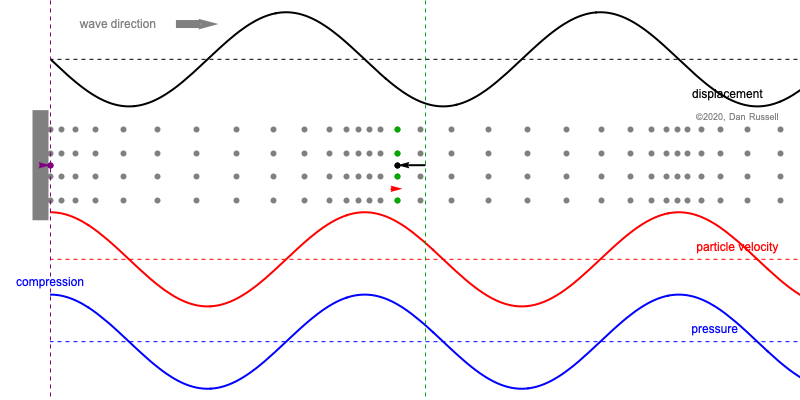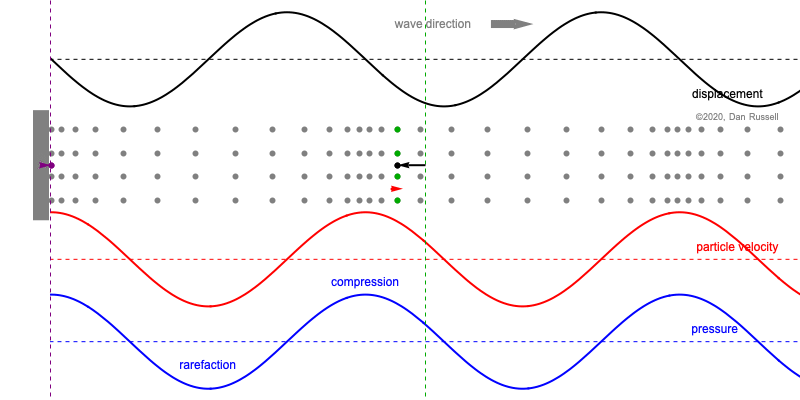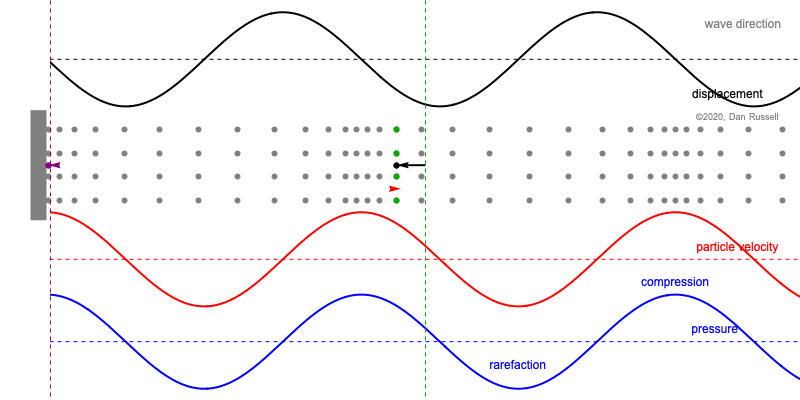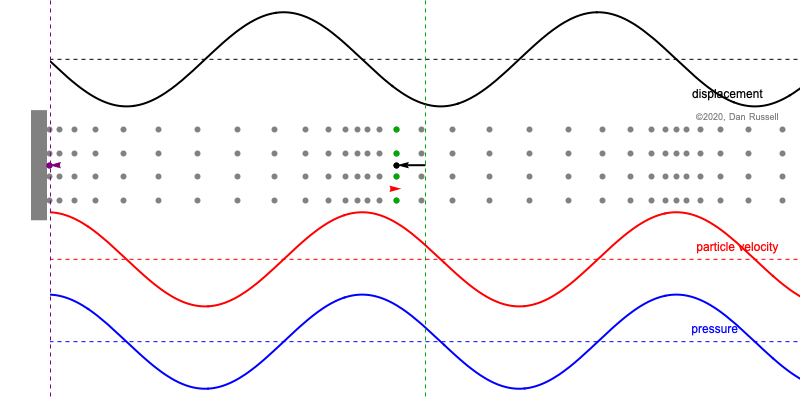
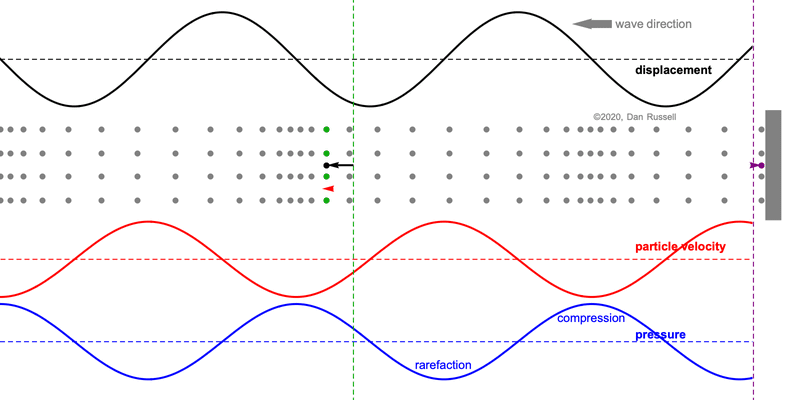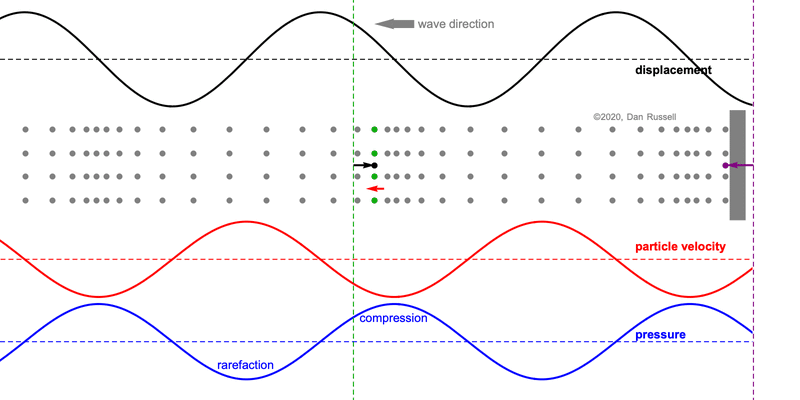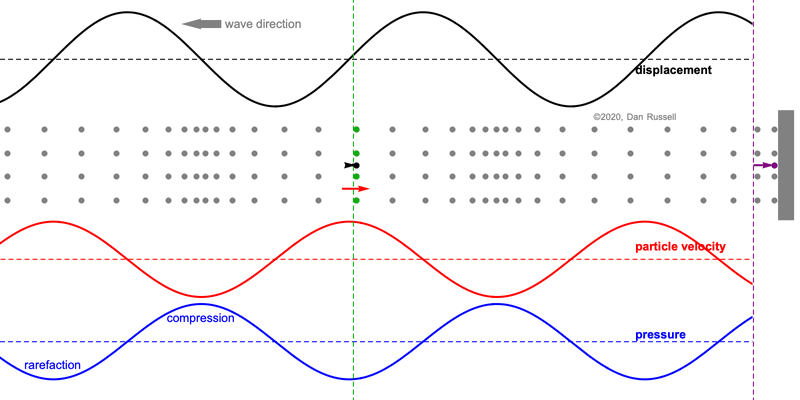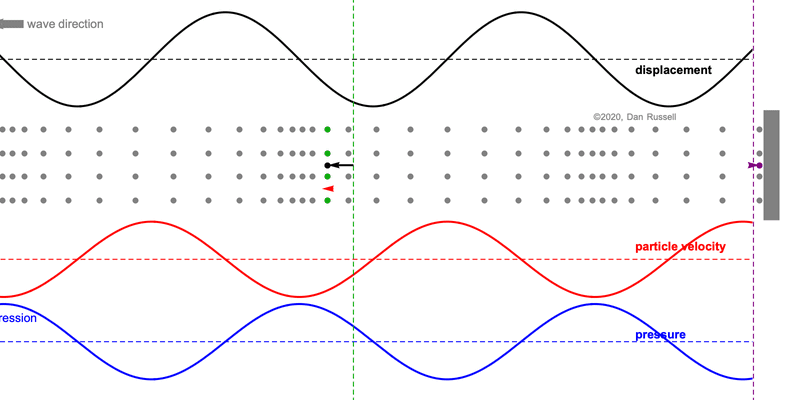
When discussing the behavior of longitudinal plane waves (i.e., sound waves air), the following statements are often made regarding the relative phase between the pressure and the fluid particle velocity^[1]

• pressure and particle velocity are in-phase for a forward traveling (right going) wave,
• but pressure and particle velocity have opposite phase for a backward traveling (left going) wave.

Mathematically this is observed the presence of a negative sign for the left going part of the wave expression. But conceptually, this can be a bit tricky to understand, especially because we tend to draw plots of displacement, velocity using the vertical axis to indicate positive values for a wave which involves longitudinal (horizontal) motion.

Click here to Show/Hide Math Equations and Explanation

If we start with an expression for pressure for a sinusoidal wave traveling in the positive \(x\)-direction, \[ p(x,t) = A e^{j(\omega t - k x)} \qquad \hbox{real part} \longrightarrow p(x,t) = A \cos(\omega t - k x) , \] the particle velocity associated with this pressure is obtained through the conservation of momentum (Euler's equation) \[ \rho\frac{\partial u}{\partial t} = - \frac{\partial p}{\partial x} \quad \longrightarrow \quad u = - \frac{1}{\rho} \int \frac{\partial p}{\partial x}\, dt \] so that the particle velocity for this sinusoidal wave traveling the positive \(x\)-direction is \[ u(x,t) = \frac{1}{\rho c} A e^{j(\omega t-kx)} \qquad \hbox{real part} \longrightarrow u(x,t) = \frac{1}{\rho c}A \cos(\omega t - k x) , \] where I've made use of the fact that the wave speed \(c=\omega/k\). Comparing the expressions for particle velocity and pressure, we see that they are exactly the same except that velocity amplitude is smaller by a factor of \(\rho c\), a quantity which is called the "characteristic impedance" of the medium through which the wave is traveling.

Now let's consider a pressure wave traveling in the negative \(x\)-direction, \[ p(x,t) = B e^{j(\omega t + k x)} \qquad \hbox{real part} \longrightarrow p(x,t) = B \cos(\omega t + k x) . \] As above, the particle velocity associated with this pressure is obtained through the conservation of momentum, so that the particle velocity for this sinusoidal wave traveling the negative \(x\)-direction is \[ u(x,t) = -\frac{1}{\rho c} B e^{j(\omega t + k x)} \qquad \hbox{real part} \longrightarrow u(x,t) = - \frac{1}{\rho c}B \cos(\omega t + k x) , \] Comparing these expressions for particle velocity and pressure, we see that now the velocity amplitude is negative indicating a 180° phase relationship between velocity and pressure.