 |
Undamped Oscillator
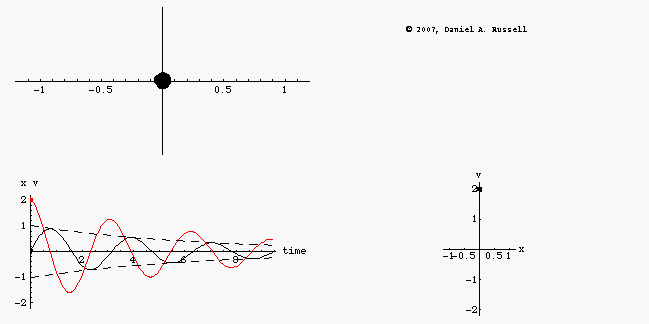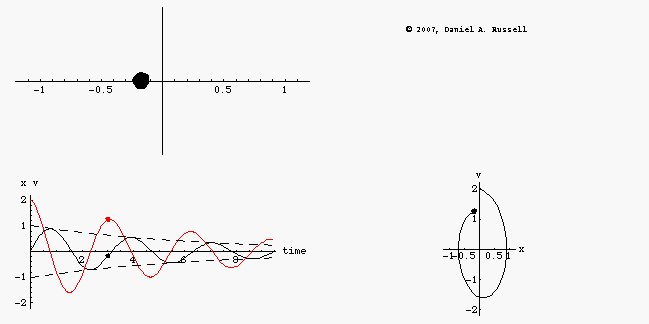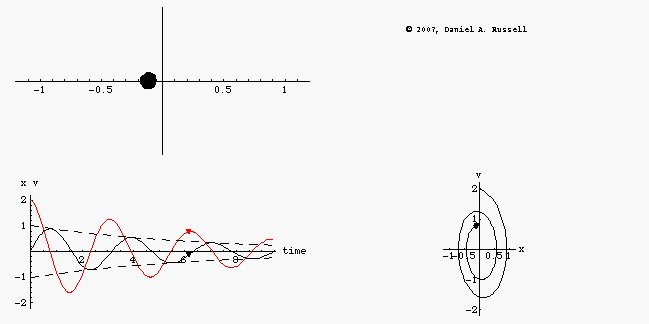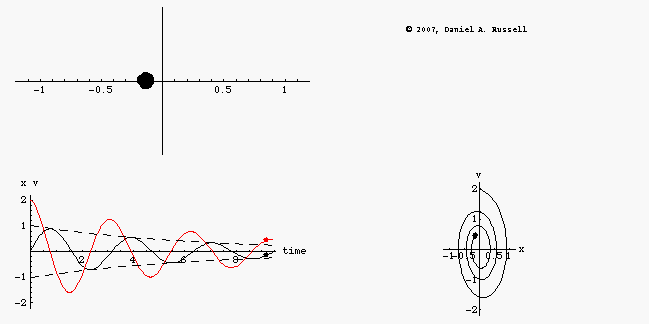
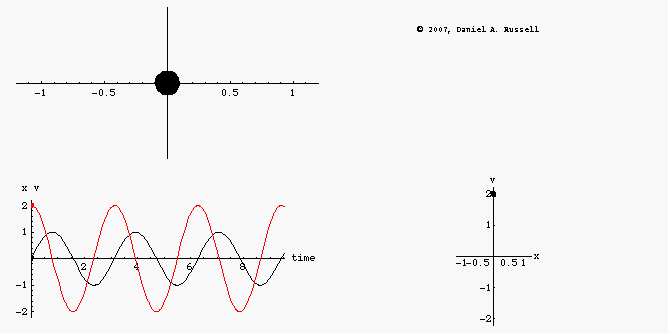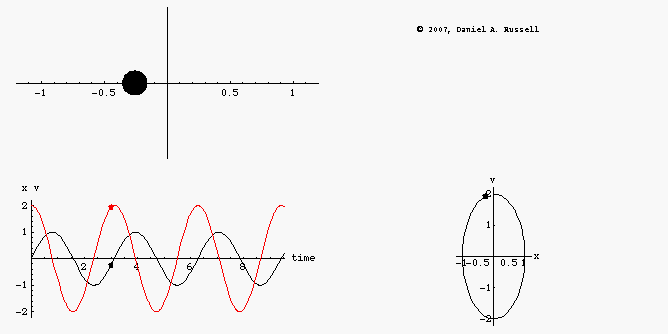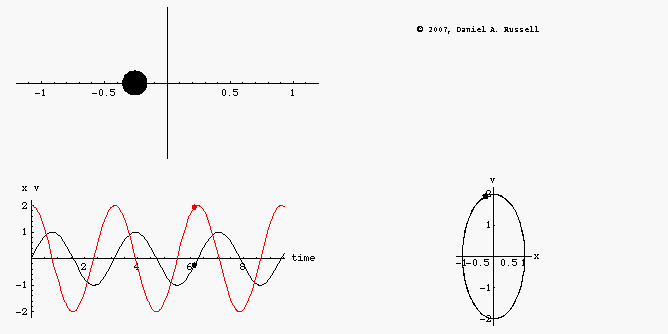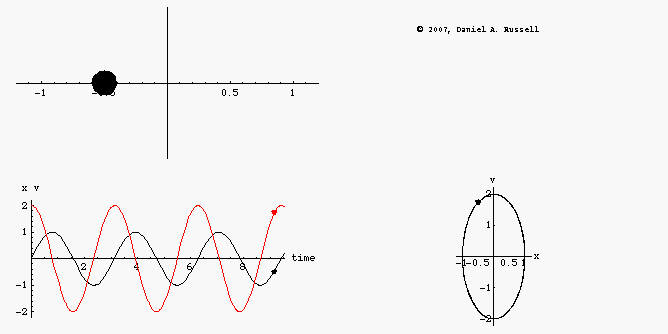
The animations at left represents the motion of an undamped oscillator. The top left animation shows the object oscillating back and forth along the x-axis. The lower left animation is a plot superimposing the position x(t) as a function of time and the velocity v(t) as a function of time on the same graph. Dots have been provided to show how both the position and velocity alternate between positive and negative maximum values as the system oscillates. The combined plots also illustrate the difference in phase between position and velocity. When the position is maximum the velocity is passing through zero, and vice versa. However, the combined plot is not as easy to visualize without making it an animation. The phase-diagram plot, shown in the lower right, shows the phase relationship between velocity and position much more clearly. As the system oscillates, the phase diagram carves out a clockwise ellipse.
|