Acoustics and Vibration Animations

Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University

All text and images on this page are ©2004-2013 by Daniel A. Russell and may not used in other web pages or reports without permission.

The content of this page was originally posted on September 7, 2012. The HTML code was modified to be HTML5 compliant on March 17, 2013.

Multiple Degree-of-Freedom Mass-Spring Systems

1-DOF Mass-Spring System

animation of single mass spring system

A single-degree-of-freedom mass-spring system has one natural mode of oscillation.

One mass connected to one spring oscillates back and forth at the frequency ω=(s/m)1/2.

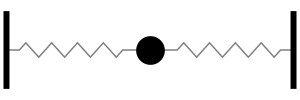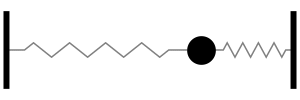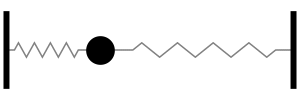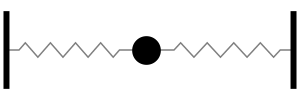
animation of one mass with two springs

One mass, connected to two springs in parallel, oscillates back and forth at the slightly higher frequency ω=(2s/m)1/2. The natural frequency is slightly higher (more oscillations per second) because the parallel springs combination has a greater stiffness than a single spring. (NOTE: the springs are in parallel - not in series - because they experience the same displacement, but not the same force).

2-DOF Mass-Spring System

animation of 2 masses, mode 1

A two degree-of-freedom system (consisting of two identical masses connected by three identical springs) has two natural modes, each with a separate resonance frequency.

The first natural mode of oscillation occurs at a frequency of ω=(s/m)1/2, which is the same frequency as the one mass, one spring system shown at the top of this page. At this requency, both masses move together, with the same amplitude and in the same direction so that the coupling spring between them is neither stretched or compressed. The system behaves like two identical single-degree-of-freedom mass-spring systems oscillating together in phase.

Alternately, you could consider this system to be the same as the one mass with two springs system shown immediately above. But, with the mass being twice as large the natural frequency, is lower by a factor of the square root of 2.

animation of 2 masses, mode 2

The second natural mode of oscillation occurs at a frequency of ω=(3s/m)1/2. At this requency, the two masses move with the same amplitude but in opposite directions so that the coupling spring between them alternately stretched and compressed. The center of the coupling spring does not move; this location is called a node.

animation of the coupled motion for two mass-spring system

In addition to the two natural modes, a 2-dof system can exhibit a coupled behavior. If one ot the masses is held at rest at its equilibrium position while the other mass is displaced from equilibrium and then both masses are released from rest, the resulting motion is coupled motion. The energy is traded back and forth between the two oscillators, and the two masses alternately switch between oscillating and being at rest. This coupled motion is not a natural mode of the 2-dof system, but is the special case for a specific set of initial conditions.

3-DOF Mass-Spring System

animation for 3 masses, mode 1

A three degree-of-freedom mass-spring system (consisting of three identical masses connected between four identical springs) has three distinct natural modes of oscillation.

The first natural mode of oscillation occurs at a frequency of ω=0.765 (s/m)1/2. At this requency, all three masses move together in the same direction with the center mass moving 1.414 times farther than the two outer masses.

animation for 3 masses, mode 2

The second natural mode of oscillation occurs at a frequency of ω=(2s/m)1/2. At this requency, the center mass does not move (this is a node) while the two outer masses move with the same amplitude but in opposite directions.

animation for 3 masses, mode 3

In the third natural mode, the outer two masses move in the same direction with the same amplitude while the center mass moves in the opposite direction with 1.414 times larger amplidue. This mode occurs at a frequency of ω=1.868 (s/m)1/2.

4-DOF Mass-Spring System

animation for 4 masses, mode 1

A four degree-of-freedom mass-spring system (consisting of four identical masses connected by five identical springs) has four distinct natural modes of oscillation.

The first natural mode of oscillation occurs at a frequency of ω=0.618 (s/m)1/2. At this requency, all four masses move together in the same direction with the inner pair moving 1.618 times as far as the outer pair. The spring between the inner pair is neither stretched nor compressed.

animation for 4 masses, mode2

The second natural mode of oscillation occurs at a frequency of ω=1.176 (s/m)1/2. At this requency, the pair of masses on the left move together but in opposite direction as the pair of masses on the right. There is a node point in the very center of the system.

animation for 4 masses, mode 3

In the third natural mode, the outer two masses move in the same direction as each other, but in the opposite direction as the inner pair of masses. The center spring again is neither compressed nor stretched. This mode has a frequency of 1.618 (s/m)1/2. There are two node locations, one between the first and second mass, and the other between the third and fourth mass.

animation for 4 masses, mode 4

In the fourth natural mode, each of the four masses alternates in direction, with the two inner masses moving with slightly greater amplitude. This mode occurs at a frequency of ω=1.902 (s/m)1/2. There are three clearly identified nodes, one each at the center of the inner three springs.