Acoustics and Vibration Animations
Daniel A. Russell
Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons License CC BY NC ND This work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License . Based on a work at http://www.acs.psu.edu/drussell/demos.html . Additional information about using this content is available at http://www.acs.psu.edu/drussell/Demos/copyright.html .


The content of this page was originally posted on July 10, 1996. Animations were updated on October 31, 1999.
HTML code was updated for accessibility and HTML5 compliance on July 29, 2025 .

Response of a 1-DOF Oscillator to a Displacement of its Base

Transient Response to Motion of the Base

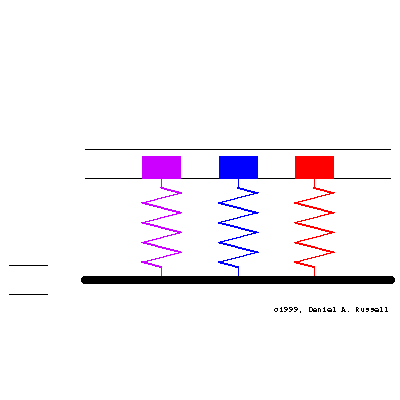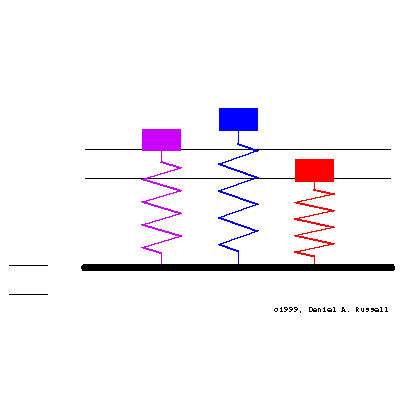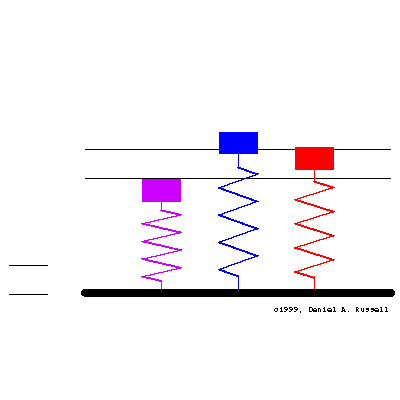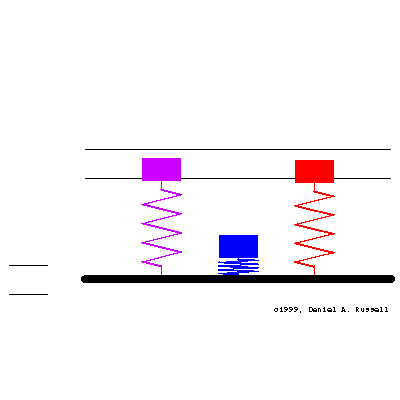
animation showing three masses oscillating in response to oscillation of the base support. See text for explanation.

Three simple 1-DOF mass-spring oscillators have natural frequencies (from left to right, matching colors) of \[ {\color{purple} f_o=0.4 } \qquad {\color{blue} f_o=1.0 } \qquad {\color{red} f_o=1.6 } \] At time t=0 the base starts moving with sinusoidal displacement \( \xi(t) = \xi_o \sin(2\pi f t) \) where the driving frequency is \( f =1.001 \). All three oscillators has a small amount of damping, so the initial transient motion decays and a steady-state is obtained.

The animation at left shows the motion of the base and the resulting motion of all three oscillators together. The masses are color coded to match the frequencies above and the plots below. The horizontal lines indicate the maximum displacement of the base.

Plots showing transition from transient to steady state motion

In all three plots below, the dashed gray curve represents the displacement of the base, while the colored curves represent the displacement of the masses.


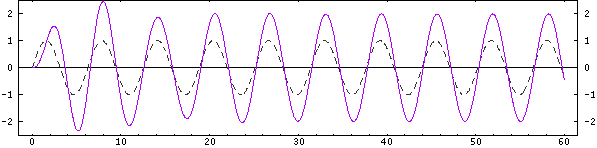
plot showing the displacement of the left mass-spring, in purple, along with the time history of the oscillating base.

Mass 1: Below Resonance

The first oscillator is being driven below its natural frequency. Its motion is in-phase with that of the base and its displacement is slightly larger than the base displacement. In terms of the input mechanical impedance as seen by the base, this oscillator provides an apparent positive added mass to the base.


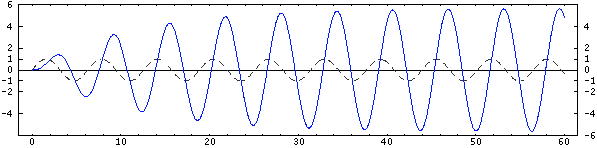
plot showing the displacement of athe middle mass-spring, in blue, along with the time history of the driving force.

Mass 2: At Resonance

The middle oscillator is being driven very near resonance. Its displacement lags that of the base by 90° and it grows until steady state is reached. In terms of the input mechanical impedance as seen by the base, this oscillator provides an apparent damping, removing vibrational energy from the base.


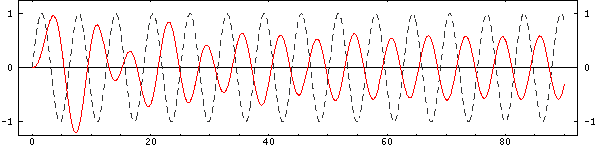
plot showing the displacement of athe right mass-spring, in red, along with the time history of the driving force.

Mass 3: Above Resonance

The third oscillator is being driven at twice its natural frequency. The transient behavior takes longer to decay. Once steady state has been achieved, the displacement is less than that of the base and it almost 180° out of phase with the base. In terms of the input mechanical impedance as seen by the base, this oscillator provides an apparent negative added mass to the base.