The Dynamic Vibration Absorber
(Tuned-Mass-Damper)
This page demonstrates the behavior of the classical undamped dynamic absorber, introduced into the literature in 1928 by J. Ormondroyd and J.P. Den Hartog. The results below were calculated using the mathematical derivation on pages 87-106 of Den Hartog's book Mechanical Vibrations, 4th Edition, (Dover, 1985).
The Classical Undamped Tuned Dynamic Absorber
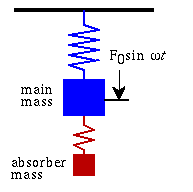
Suppose a sinusoidal force \( F_o \sin(\omega t) \) acts on an undamped main mass-spring system (without the absorber mass attached). When the forcing frequency equals the natural frequency of the main mass the response is infinite. This is called resonance, and it can cause severe problems for vibrating systems.
When an absorbing mass-spring system is attached to the main mass and the resonance of the absorber is tuned to match that of the main mass, the motion of the main mass is reduced to zero at its resonance frequency. Thus, the energy of the main mass is apparently "absorbed" by the tuned dynamic absorber. It is interesting to note that the motion of the absorber is finite at this resonance frequency, even though there is NO damping in either oscillator. This is because the system has changed from a 1-DOF system to a 2-DOF system and now has two resonance frequencies, neither of which equals the original resonance frequency of the main mass (and also the absorber).
If no damping is present, the response of the 2-DOF system is infinite at these new frequencies. While this may not be a problem when the machine is running at its natural frequency, an infinite response can cause problems during startup and shutdown. A finite amount of damping for both masses will prevent the motion of either mass from becoming infinite at either of the new resonance frequencies. However, if damping is present in either mass-spring element, the response of the main mass will no longer be zero at the target frequency.
Animation of the main mass and dynamic absorber at three operating frequencies.

The 2-DOF system has two natural frequencies, corresponding to the two natural modes of vibration for the system. In the lower frequency mode both masses move in the same direction, in-phase with each other. In the higher frequency mode the two masses move in opposite direction, 180° out of phase with each other. The animation below shows the motion of the 2-DOF system at normalized forcing frequencies of
- \( f_{\rm left}=0.67 \) (in-phase mode),
- \( f_{\rm middle}=1 \) (undamped classical tuned dynamic absorber),
- \( f_{\rm right}=1.3 \) (opposite-phase mode).
Frequency response plots for the main mass and absorber mass
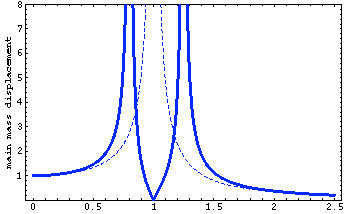
The plots below show the displacements as a function of normalized frequency (driving frequency divided by natural frequency of main mass). The plot on the left below shows the response of the main (blue) mass-spring system to which the sinusoidal driving force is applied. The dashed curve shows the displacement response of the undamped main mass alone (without the second attached absorber). Notice that when the driving frequency matches the natural frequency, the response of the main system (dashed curve) is infinite. The thick curve An absorber mass (20% of the main mass) is tuned to the resonance frequency of the main mass and attached. The thick curve represents the displacement of the main mass with the classical undamped tuned dynamic absorber attached. Notice that when the dynamic absorber is present, the main mass has zero displacement at the original problem frequency. Notice, also, that there are now two new resonance frequencies.
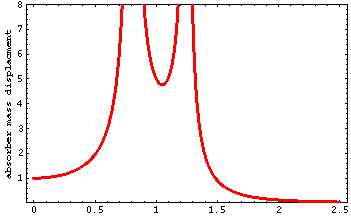
The red curve represents the displacement of the absorber mass. Notice that the displacement is infinite at the same two resonance frequencies, but that the response at the target frequency is finite (approximately 4.8).