Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University
This work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://www.acs.psu.edu/drussell/demos.html.
The content of this page was originally posted on January 24, 2012. The HTML code was modified to be HTML5 compliant on March 16, 2013.
The tuning fork vibrational modes shown below were extracted from a COMSOL Multiphysics computer model built by one of my former students (Eric Rogers) as part of the final project for the structural vibration component of PHYS-485, Acoustic Testing & Modeling, a course that I taught for several years while I was a member of the physics faculty at Kettering University.
The fundamental mode of vibration is the mode most commonly associated with tuning forks; it is the mode shape whose frequency is printed on the fork, which in this case is 426 Hz. The two tines of the fork alternately move toward and away from each other, each bending like a cantilever beam, fixed at the stem and free at the other end. This is a symmetric mode, since the two tines are mirror images of each other.
A video on my YouTube Channel shows the slow-motion oscillation (shot with a high speed camera at 1200fps) of a 125 Hz tuning fork vibrating in its fundamental mode of vibration.
When vibrating in the fundamental mode, it would appear that the stem of the fork is stationary. However, the stem actually vibrates up and down at the fundamental frequency as well as at the second harmonic, 852 Hz - twice the frequency of the fundamental (even there is no vibrational mode of the fork at this frequency). This stem motion is very small, and difficult to feel if you place a finger tip at the bottom of the stem. But, it can be effectively demonstrated by touching the stem of a vibrating fork to a table top, door, or piano soundboard.
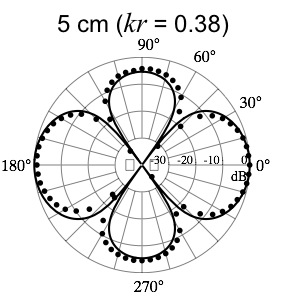The fundamental vibration mode of a tuning fork radiates sound as a longitudinal (or linear) quadrupole sound source[1] with a well-defined transition between the near-field and far-field radiated patterns.[2,3] The plot at left shows the near-field measured directivity pattern (dots) representing the sound pressure level as a function of angle around the fork along with the theoretical model (curve) for a longitudinal quadrupole.[2]
This is the second most commonly heard vibrational mode. It results from striking the tines of the fork against a hard object. This mode is the second mode shape for a clamped-free bar, and it has a much higher frequency (roughly 6.26 times higher than the fundamental). The clang tone may sound louder than the fundamental because the human ear is much more sensitive to frequencies between 1000 Hz and 4000 Hz while the ear does not hear frequencies below 500 Hz very well.
This is also a symmetric mode, since the two tines are mirror images of each other.
In addition to the familiar symmetric fundamental and clang modes, a tuning fork can also exhibit a family of in-plane bending modes, similar to a the vibrational modes of a clamped-free solid bar. Instead of each tine oscillating as a separate clamped-free bar, the entire fork vibrates as one object. The animations at right show the first three such clamped-free mode shapes for the tuning fork. The frequencies are (from left to right) 385 Hz, 2171 Hz, and 4772 Hz. Notice that the first of these modes has a frequency lower than that of the fundamental mode at 426 Hz.
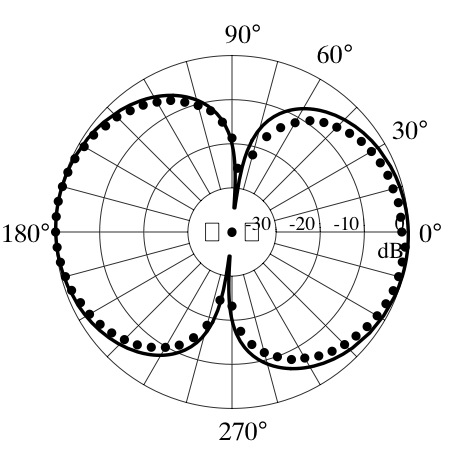The first in-plane bending mode (385 Hz) radiates sound as a dipole source.[2] The plot at left shows the measured directivity pattern (dots) representing the sound pressure level as a function of angle around the fork along with the theoretical model (curve) for a dipole source.[2]
In addition to the in-plane bending modes, a tuning fork will also exhibit several out-of-plane bending modes where the fork acts like a solid bar, vibrating perpendicularly to the plane of the tines. Frequencies (left to right): 457 Hz, 2861 Hz. The lowest of these modes is very close to the fundamental frequency.
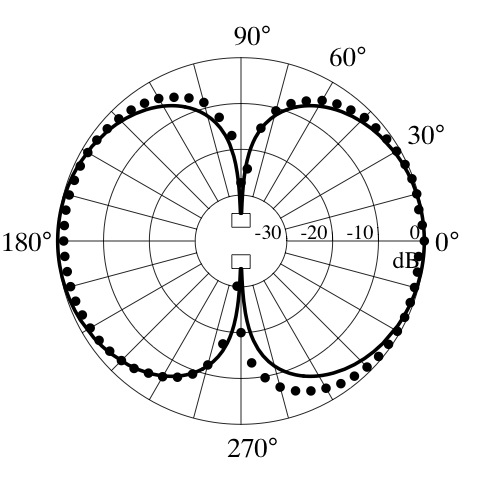The first out-of-plane bending mode (457 Hz) radiates sound as a dipole source. The plot at left shows the measured directivity pattern (dots) representing the sound pressure level as a function of angle around the fork along with the theoretical model (curve) for a dipole source.[2]
A fork, clamped at the stem, will also exhibit asymmetric out-of-plane modes where the two tines oscillate perpendicular to the plane of the fork, but in opposite directions to each other. The fork essentially twists back and forth - rather like the torsional twisting modes of a solid bar. The frequencies for these two modes of vibration are 537 Hz and 3102 Hz. This vibrational mode is discussed briefly by Backus in his text on musical acoustics.[4]
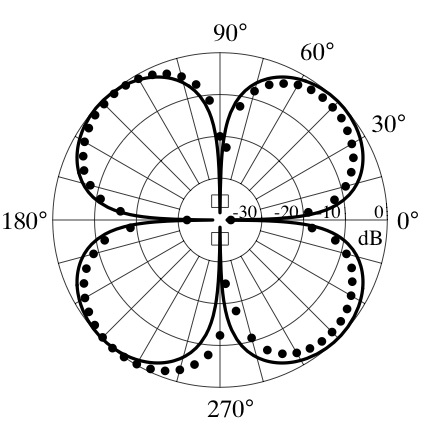The first out-of-plane bending mode (537 Hz) radiates sound as a lateral quadrupole source. The plot at left shows the measured directivity pattern (dots) representing the sound pressure level as a function of angle around the fork along with the theoretical model (curve) for a lateral quadrupole.[2]
References