The animations on this page were inspired after reading: Roger Knobel Introduction to the Mathematical Theory of Wave Motion, (American Mathematical Society, 2000), pp. 31-35.
Solitons (Solitary Waves)
In 1834, John Scott Russell, a Scottish naval enginer, was observing the passage of a boat along a canal and noticed a very strange type of wave traveling along the canal. His famous (and oft repeated) summary of the event[1] states . . .
I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped - not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation.
Fascinated by what he had observed, Russell constructed a 30-foot wave tank in his back yard and carried out experiments. He made the following observations:
- These "solitary" waves are stable, and can travel over very large distances without changing their shape, neither decreasing in amplitude nor breaking as waves in water often do.
- The speed of the wave depends on the height of the wave.
- These waves don't obey superposition. When a taller (faster) wave overtakes a shorter (slower) wave, they don't combine and add together. Instead they appear to swap places with the faster wave appearing to jump through the slower one.
The mathematical theory explaining the existince of these solitary heaps of water was first deveoped by Boussinesq[2] in 1871 and Rayleigh[3] in 1876. However, it is the form of the equation and its solutions as developed by Koreweg and de Vries[4] in 1895 that is most commonly used to describe the waves that have become known as "solitons". The equation of motion for these waves can be written in dimensionless form as $$ \frac{\partial x}{\partial t} + u\frac{\partial u}{\partial x} + \frac{\partial^3 u}{\partial t^3}=0 $$ with wave functions satisfying this equation of motion having the form $$ u(x,t) = 3c\,\hbox{sech}^2\biggl(\frac{\sqrt{c}}{2}(x - ct)\biggr) $$ where the wave speed c depends on the height of the wave pulse.


 The animation at left shows what happens when these two solitons meet in the same medium. The top trace (thin gray line) shows what we would expect to see if the wave pulses simply interfered with each other through superposition. Of course, if these were linear waves, they would both be traveling with the same speed the tall one would not overtake the shorter one. The bottom trace (thick black line) shows what actually happens to these two solitary waves. As the faster, taller pulse catches up to the shorter, slower pulse, the two do not simply add together. Instead, the taller pulse appears to jump through the shorter one and they switch places. After they "collide" they keep moving each with their own speeds but they are not in the relative locations we would have expected the to be in had they simply passed through eachother.
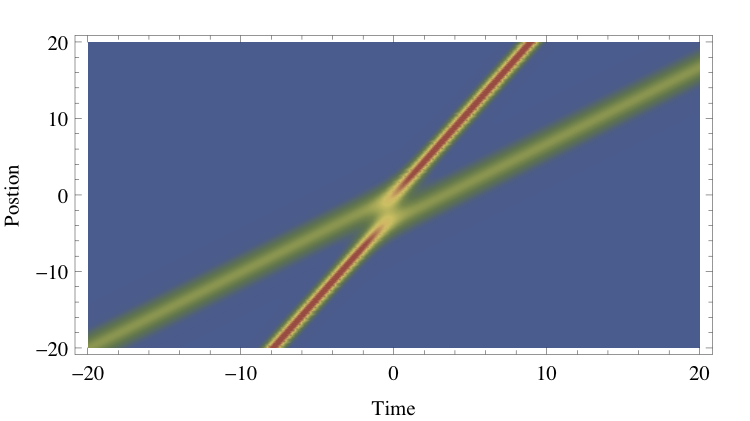
The contour plot at right shows the traces of the two pulses as they collide, and it is easy to see that the paths of the two pulses appear to jump and change places rather than just pass through each other.
The animation at left shows what happens when these two solitons meet in the same medium. The top trace (thin gray line) shows what we would expect to see if the wave pulses simply interfered with each other through superposition. Of course, if these were linear waves, they would both be traveling with the same speed the tall one would not overtake the shorter one. The bottom trace (thick black line) shows what actually happens to these two solitary waves. As the faster, taller pulse catches up to the shorter, slower pulse, the two do not simply add together. Instead, the taller pulse appears to jump through the shorter one and they switch places. After they "collide" they keep moving each with their own speeds but they are not in the relative locations we would have expected the to be in had they simply passed through eachother.
The contour plot at right shows the traces of the two pulses as they collide, and it is easy to see that the paths of the two pulses appear to jump and change places rather than just pass through each other.