The Simple Harmonic Oscillator
Simple Harmonic Motion
In order for mechanical oscillation to occur, a system must posses two quantities: elasticity and inertia. When the system is displaced from its equilibrium position, the elasticity provides a restoring force such that the system tries to return to equilibrium. The inertia property causes the system to overshoot equilibrium. This constant play between the elastic and inertia properties is what allows oscillatory motion to occur. The natural frequency of the oscillation is related to the elastic and inertia properties by:
\[ \omega_o = 2\pi f_o = \sqrt{\frac{\hbox{elastic modulus}}{\hbox{inertia}}} \]The simplest example of an oscillating system is a mass connected to a rigid foundation by way of a spring. The spring constant \( k \) provides the elastic restoring force, and the inertia of the mass <\( m \) provides the overshoot. By applying Newton's second law \( F = ma \) to the mass, one can obtain the equation of motion for the system: \[ m \frac{d^2 x}{dt^2} + kx = 0 \qquad \longrightarrow \qquad \frac{d^2 x}{dt^2} + \frac{k}{m}x = 0 \qquad \longrightarrow \qquad \frac{d^2 x}{dt^2} + \omega_o^2 x = 0 \] where \( \omega_o = \sqrt{k/m} \) is the natural oscillating frequency.
The solutions to this equation of motion takes the form \[ x(t) = x_{\rm max} \cos(\omega_o t + \phi) \] where \( x_{\rm max} \) is the amplitude of the oscillation, and \( \phi \); is the phase constant of the oscillation. Both \( x_{\rm max} \) and \( \phi \) are constants determined by the initial conditions (intial displacement and velocity) at time <\( t=0 \) when one begins observing the oscillatory motion. <\p>
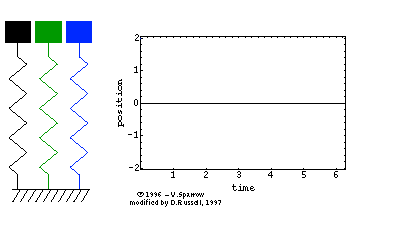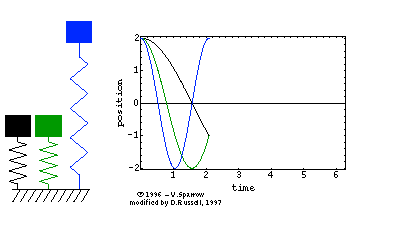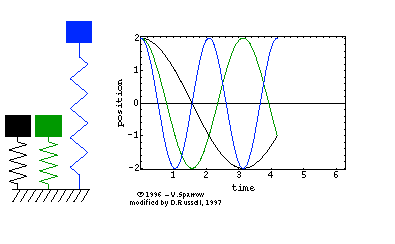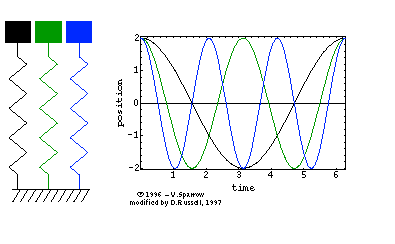
The animation at right shows the simple harmonic motion of three undamped mass-spring systems, with natural frequencies (from left to right) of \( \omega_o \), \( 2\omega_o \), and \( 3\omega_o \). All three systems are initially at rest, but displaced the same distance from equilibrium.
The period of the oscillatory motion is defined as the time required for the system to start one position, complete a cycle of motion and return to the starting position.
⇒ From the position versus time plot, can you determine the period for each of the three oscillators?
Energy Swapping
The elastic property of the oscillating system (spring) stores potential energy \[ \frac{1}{2} k x^2 = \frac{1}{2} k x_{\rm max}^2 \cos^2(\omega_o t + \phi) \] and the inertia property (mass) stores kinetic energy \[ \frac{1}{2} m v^2 = \frac{1}{2} m \omega_o^2 x_{\rm max}^2 \sin^2(\omega_o t + \phi) \] As the system oscillates, the total mechanical energy in the system trades back and forth between potential and kinetic energies. The total energy in the system, however, remains constant, and depends only on the spring contant and the maximum displacement (or mass and maximum velocity \( v_{\rm max} = \omega x_{\rm max} \) \[ \frac{1}{2} k x^2 + \frac{1}{2} m v^2 = \frac{1}{2} k x_{\rm max}^2 \cos^2(\omega_o t + \phi) + \frac{1}{2} m \omega_o^2 x_{\rm max}^2 \sin^2(\omega_o t + \phi) \ . \] Since \( \omega_o = \sqrt{k/m} \) this becomes \[ \frac{1}{2} k x^2 + \frac{1}{2} m v^2 = \frac{1}{2} k x_{\rm max}^2 \Bigl( \cos^2(\omega_o t + \phi) + \sin^2(\omega_o t + \phi) \Bigr) = \frac{1}{2} k x_{\rm max}^2 = \frac{1}{2} m v_{\rm max}^2 \ . \]

The animation at right (courtesy of Vic Sparrow) shows how the total mechanical energy in a simple undamped mass-spring oscillator is traded between kinetic and potential energies while the total energy remains constant.
