Plane Waves and Evanescent Waves
(Sound Radiation from a Plate)

A plane wave is a wave that propagates in only one direction, with wavefronts that are planes perpendicular to the direction in which the wave is traveling. Along those planar wavefronts, the pressure (or displacement from equilibrium) has the same value. An evanescent wave doesn't propagate but instead decays exponentially with distance.

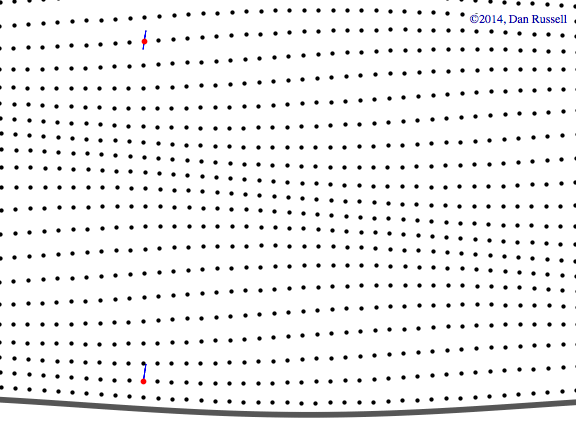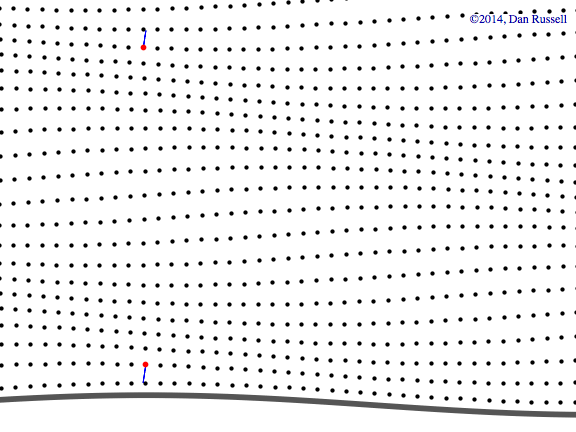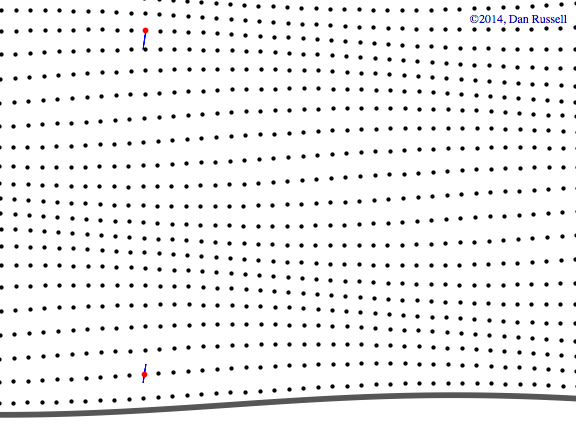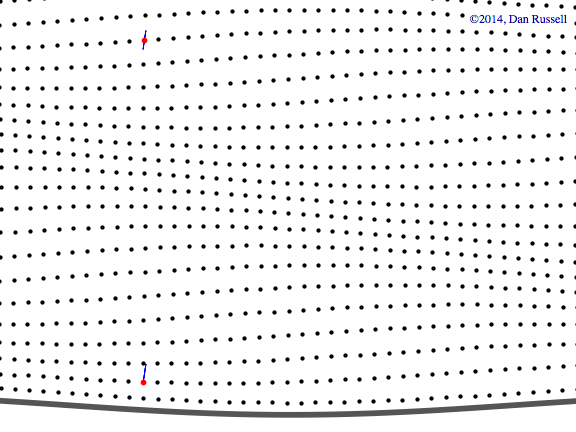
Plane wave in \(+x\) direction

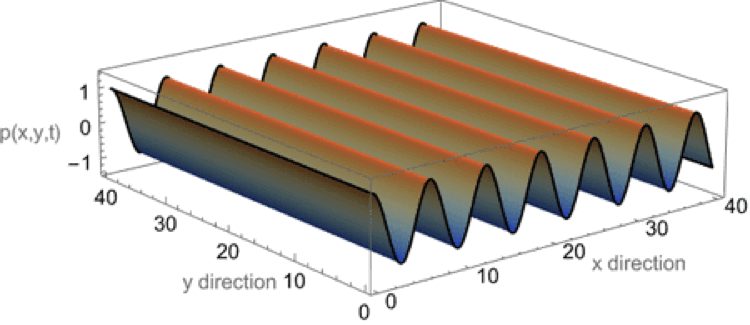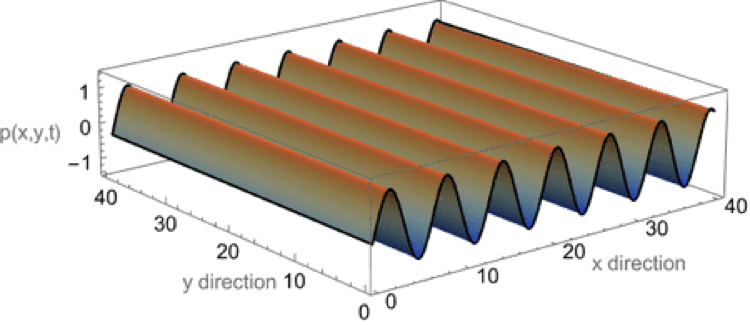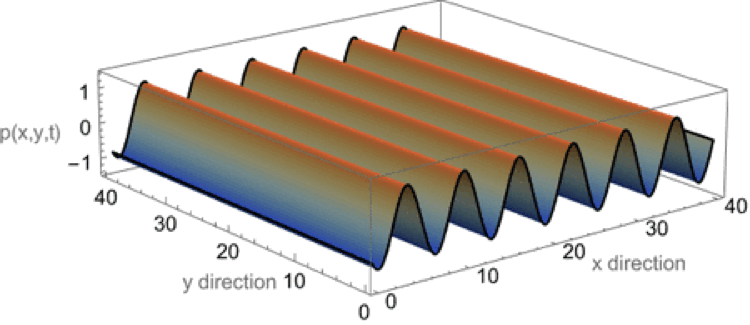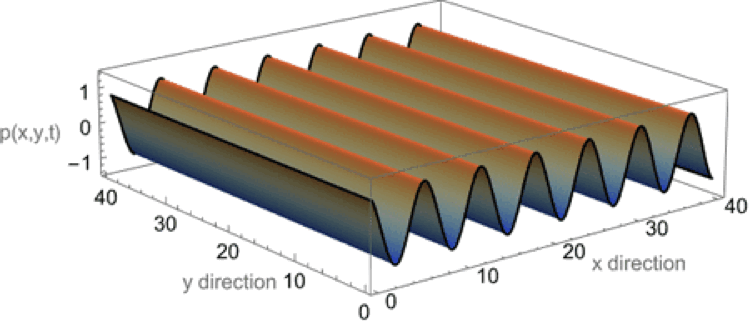
This first animation shows a plane wave propagating in the +x direction. The equation describing the plane wave is \( p(x,y,t)=A^{-i(\omega t - k_x x)} \) with the real part carrying the physical meaning. There is no variation in the amplitude along the y-axis as the wave travels parallel to the x-axis.

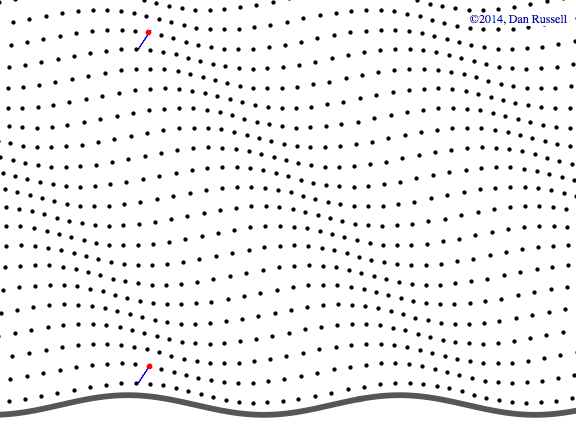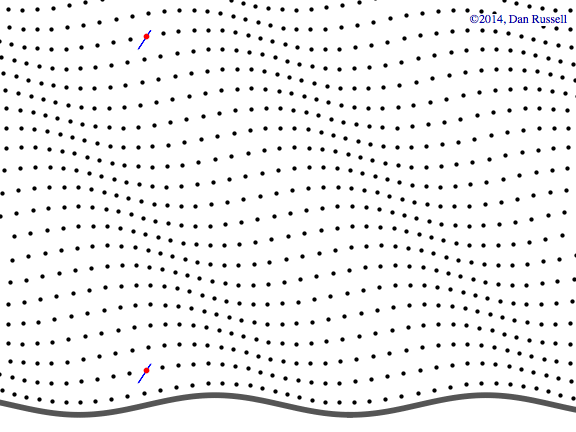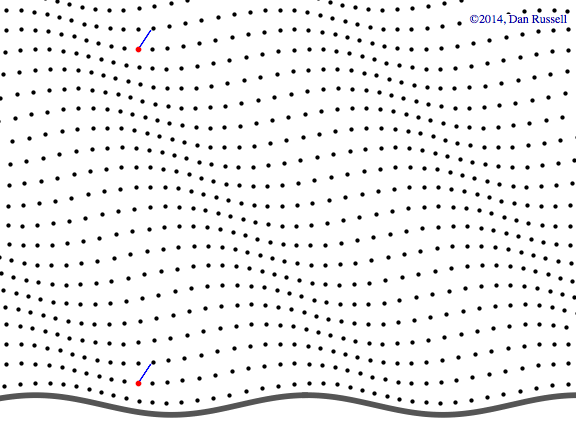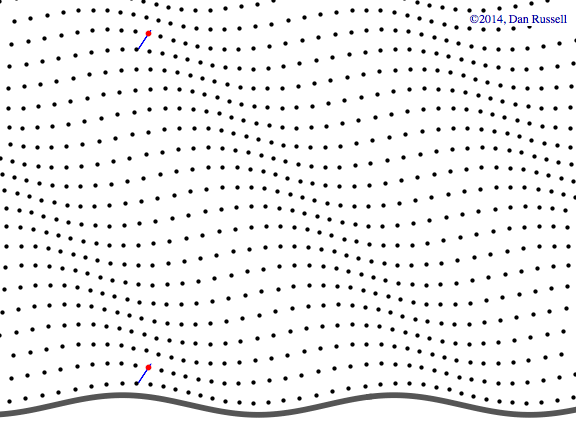
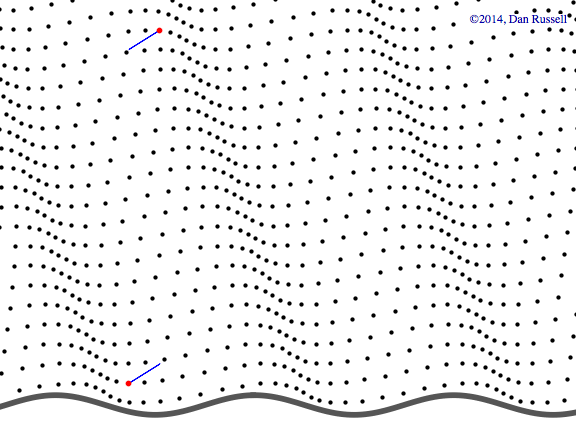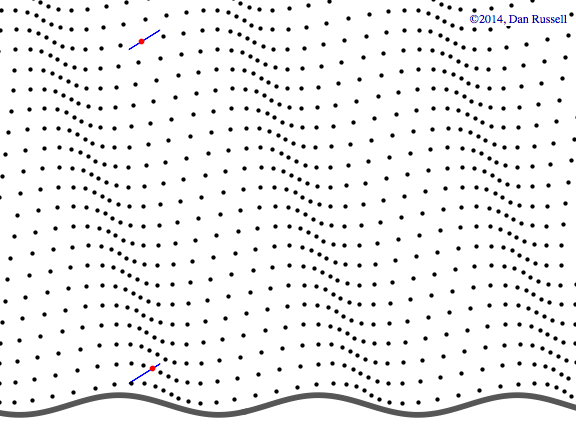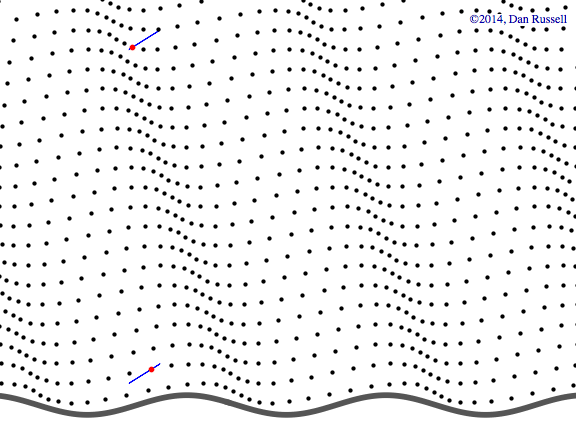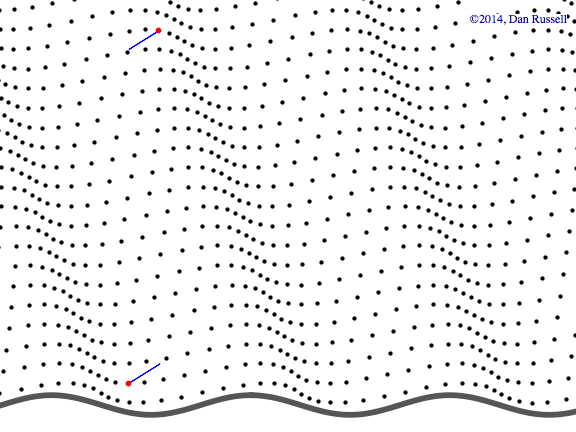
Plane wave in both x-y plane

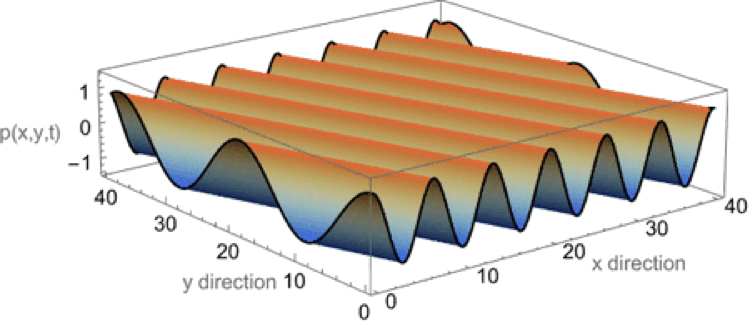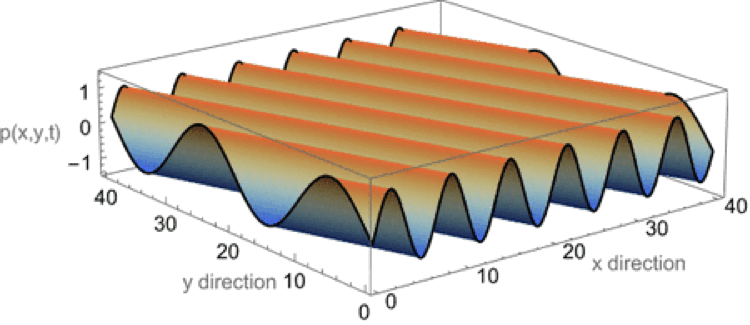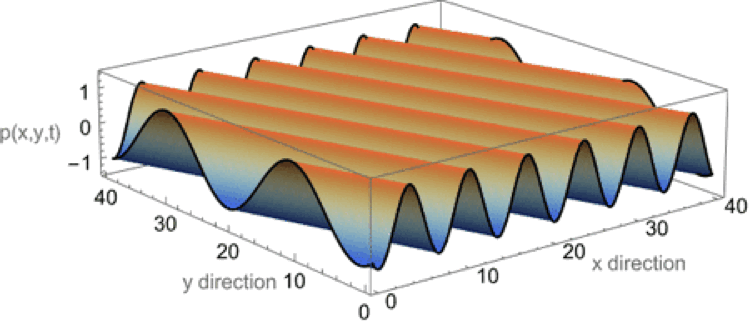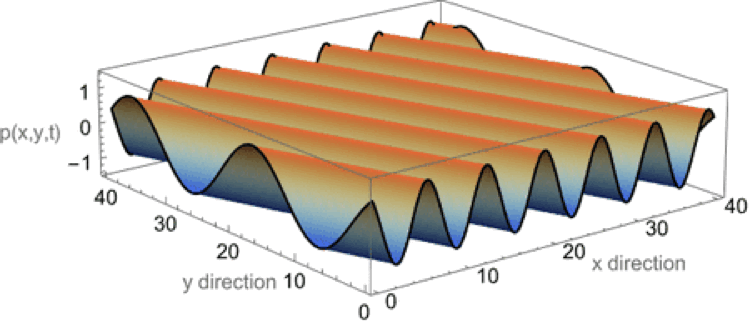
This animation shows a plane wave propagating in the x-y plane with components in both the x and y directions. The wave function is \( p(x,y,t)=A^{-i(\omega t - k_x x - k_y y)} \) and the animations shows traces of the wave along the x and y axes. In this example, the plane wave is propagating at an angle of 19^o from the x-axis, and the trace velocity of the wave along the y-axis is noticeably faster than the trace velocity of the wave along the x-axis. The trace wavelength in the y-direction is longer than the trace wavelength along the x-direction.

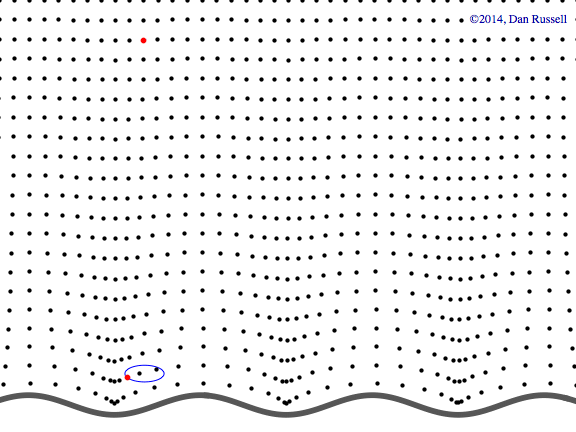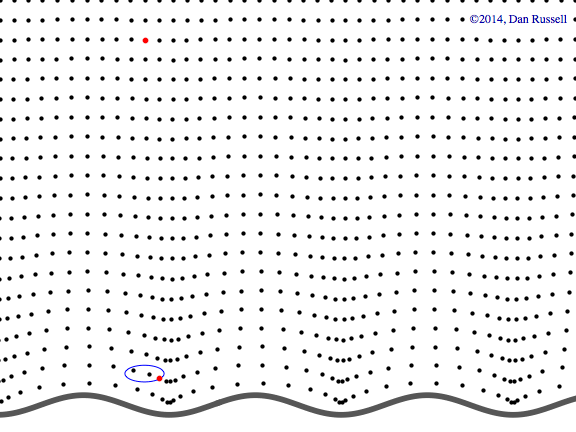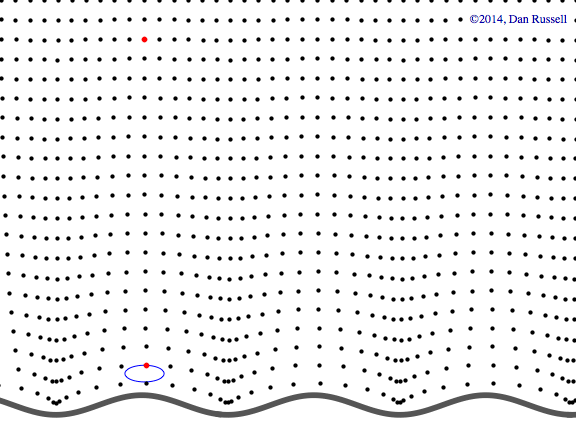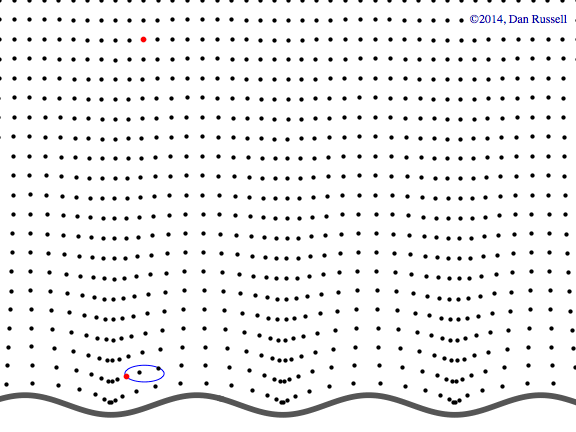
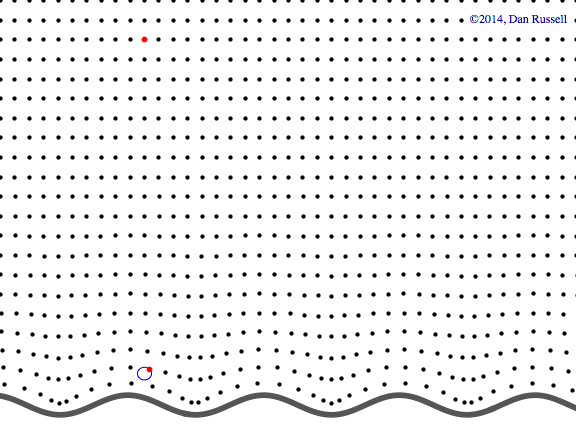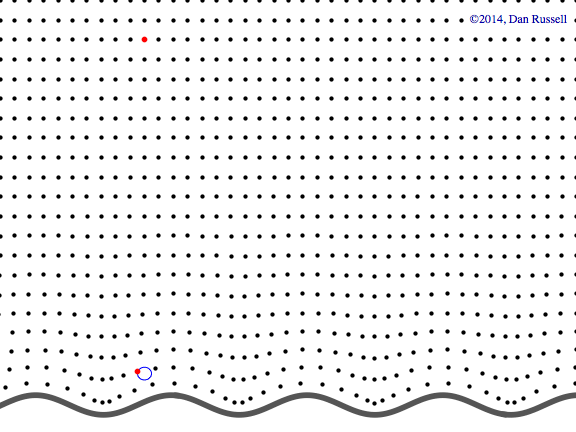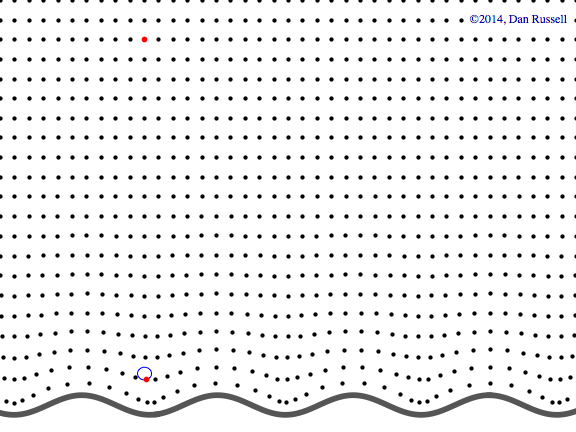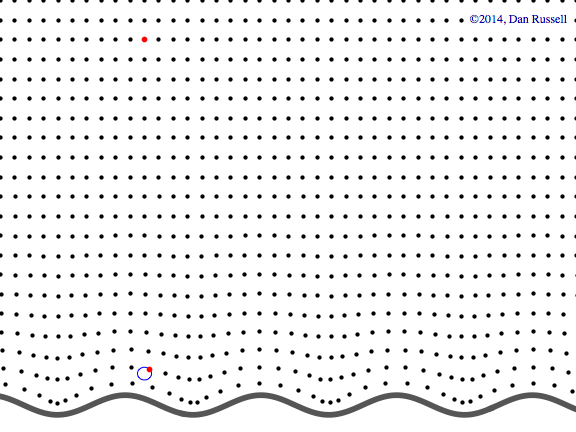
Evanescent wave in the x-y plane

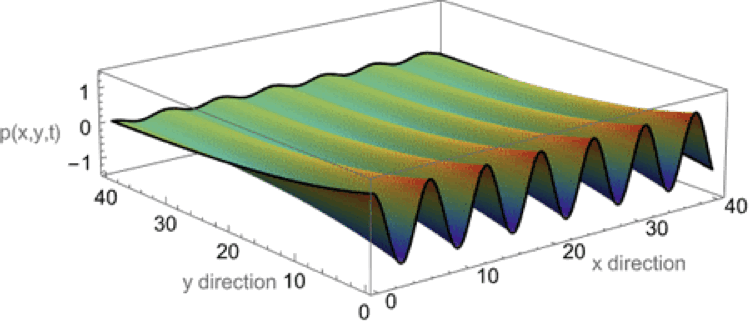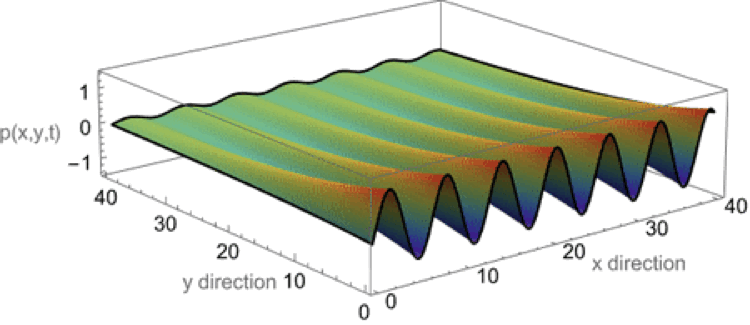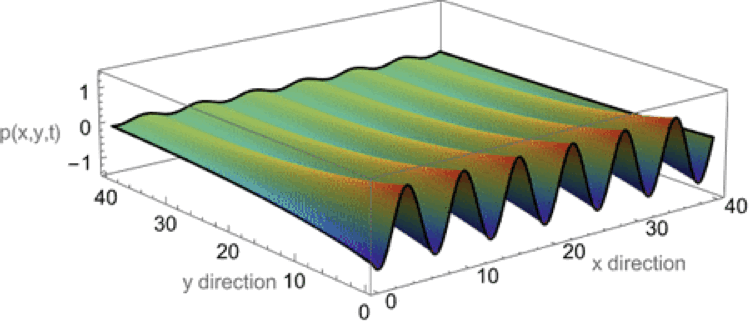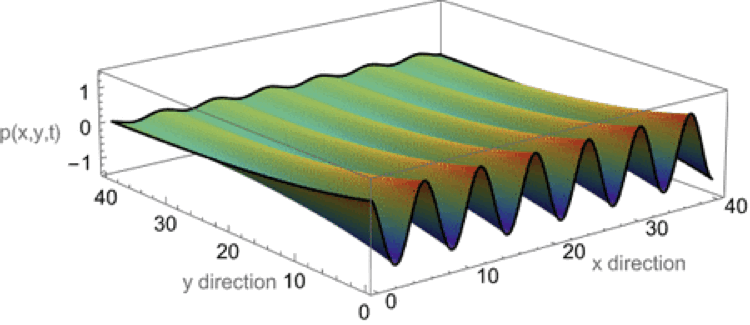
This animation shows a evanescent wave with a trace velocity along the x-axis, but which decays exponentially in the y-direction. The wavenumber k_y in the y-direction is imaginary, resulting in disturbance of the form \( p(x,y,t)=Ae^{-k_y y}e^{-i(\omega t - k_x x)} \) that exponentially decays in the y-direction, while traveling in the x-direction.

Sound Radiation from Bending Waves on a Plate

Flexural bending waves in a plate are transverse waves, in that the displacement of the plate is perpendicular (or transverse) to the direction of wave propagation. When a flexural bending wave is traveling along a plate, the surround fluid is displaced due to the wave in the plate, and longitudinal sound waves may travel through the medium away from the plate.

The speed of longitudinal sound waves in a fluid depends on the elastic and inertia properties of the fluid, and for a homogeneous fluid (or gas) at a specific pressure and temperature, the speed of sound in the fluid is a constant. The speed of flexural bending waves in a thin plate depends on the plate materials (density and elastic moduli), the plate thickness, and also on the frequency of the wave. Flexural bending waves with higher frequencies (shorter wavelengths) travel faster than lower frequency (long wavelength) waves. The radiation of sound from flexural bending waves in a plate depends on whether the speed of bending waves in the plate is faster or slower than the speed of sound in the fluid.

Plate Wave Speed (Trace Velocity) Faster than Sound Speed in Fluid

The animations below illustrate the sound radiation from flexural Bending waves traveling in the +x direction (to the right) on an infinite thin plate. The plate wave motion is shown as the thick black wave pattern at the bottom of each animation. The particles in the fluid medium above the plate oscillate in response to this plate motion. I have identified two particles with red dots to highlight particle motion both near and far from the plate. For each of these two particles, I have also indicated the trajectory of their motions with a blue curve.

Click on any of the animations below to open a larger version in a new window/tab.

c_plate = 5 c_fluid (plane waves)

The speed of the wave in the plate (trace velocity in x-direction) is 5 times the speed of sound in the fluid above the plate, and the flexural bending wave has a wavelength much longer than the wavelength of the sound wave in the fluid. A plane wave is radiated almost straight upward, nearly perpendicular to the plate surface. The particles at all locations in the fluid oscillate back and forth along a straight line parallel to the direction of wave propagation.

c_plate = 1.5 c_fluid (plane waves)

The speed of the wave in the plate (trace velocity in x-direction) is 1.5 times the speed of sound in the fluid above the plate, and the flexural bending wave has a wavelength slightly longer than the wavelength of the sound wave in the fluid. A plane wave is radiated at roughly 45^o from the horizontal. The particles at all locations in the fluid oscillate back and forth along a straight line parallel to the direction of wave propagation.

c_plate = 1.1 c_fluid (plane waves)

The speed of the wave in the plate (trace velocity in x-direction) is now 1.1 times the speed of sound in the fluid above the plate, and the flexural bending wave has a wavelength nearly the same as the wavelength of the sound wave in the fluid. A plane wave is radiated at roughly 25^o from the horizontal. The particles at all locations in the fluid oscillate back and forth along a straight line parallel to the direction of wave propagation.

Plate Wave Speed (Trace Velocity) Slower than Sound Speed in Fluid

As the speed of the transverse bending wave in the plate decreases and approaches the speed of sound in the fluid, the direction of the radiated plane wave rotates from upward, perpendicular to the plate surface, to being parallel to the plate surface, when the two speeds are exactly the same. The condition when the flexural bending wave speed in the plate equals the speed of sound in the fluid is called "coincidence" since the two wave speeds "coincide". When the speed of the flexural bending wave in the plate is slower than the speed of sound in the fluid, the plane wave cannot bend back toward the plate surface, but instead the wave becomes evanescent with the wave amplitude decaying exponentially in the vertical direction away from the plate surface. Particles in the fluid near the plate surface move in counter-clockwise ellipses as the flexural wave passes by, while particles far from the plate surface don't move at all.

c_plate = 1.03 c_fluid (plane waves)

Just above coincidence, the speed of the wave in the plate (trace velocity in x-direction) is 1.03 times the speed of sound in the fluid, and the flexural bending wave has a wavelength almost exactly the same as the wavelength of the sound wave in the fluid. A plane wave is almost parallel to the plate surface. The particles at all locations in the fluid oscillate back and forth along a straight line parallel to the direction of wave propagation.

c_plate = 0.95 c_fluid (evanescent wave)

Now the plate wave speed is just barely slower than the sound speed in air, (c_plate=0.95 c_fluid). There is now no radiated plane wave. Instead there is an evanescent wave which travels in the x-direction parellel to the plate, but which decays exponentially in the y-direction away from the plate. In the near-field close to the plate surface, the trajectory of the particle motion is a counter-clockwise ellipse, showing that the primary effect of the flexural bending wave is to simply "slosh" the fluid back and forth as it passes by.

c_plate = 0.75 c_fluid (evanescent wave)

Finally the plate wave speed is just 75% of the sound speed in air, and again there is no radiated plane wave. An evanescent wave travels in the x-direction parellel to the plate, but which decays exponentially in the y-direction away from the plate. In the near-field close to the plate surface, the trajectory of the particle motion is a counter-clockwise circle, showing that the primary effect of the flexural bending wave is to simply "slosh" the fluid back and forth as it passes by.

References

L. Cremer, M. Heckl, and B.A.T. Petersson, Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies, 3rd Edition, (Springer-Verlag, Berlin, 2005), pp. 461-464.
Earl G. Williams, Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography, (Academic Press, 1999), pp. 18-31.

Plane Waves and Evanescent Waves (Sound Radiation from a Plate)