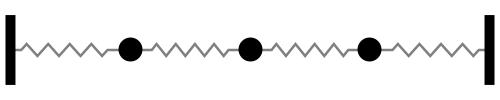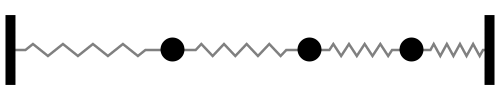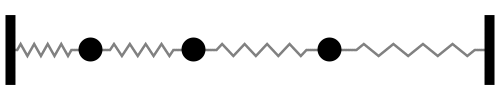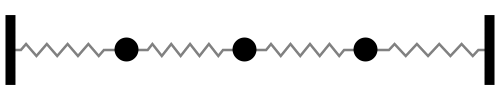
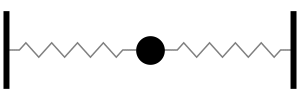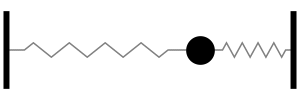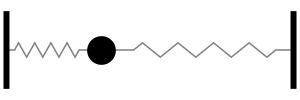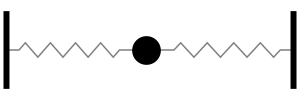
|
Acoustics and Vibration Animations
Daniel A. Russell, Ph.D. Graduate Program in Acoustics The Pennsylvania State University All text and images on this page are ©2004-2011 by Daniel A. Russell and may not used in other web pages or reports without permission. | 
|
 |
One mass, connected to two springs in parallel, oscillates back and forth at the frequency ω=(2s/m)1/2.
(note: the springs are in parallel - not in series - because they experience the same displacement, but not the same force). |
 |
The first natural mode of oscillation occurs at a frequency of ω=(s/m)1/2. At this requency, both masses move together, with the same amplitude and in the same direction so that the coupling spring between them is neither stretched or compressed. |
 |
The second natural mode of oscillation occurs at a frequency of ω=(3s/m)1/2. At this requency, the two masses move with the same amplitude but in opposite directions so that the coupling spring between them alternately stretched and compressed. The center of the coupling spring does not move; this location is called a node. |
 |
If one ot the masses is held at rest at its equilibrium position while the other mass is displaced and then released from rest, the resulting motion is coupled motion. The energy is traded back and forth between the two oscillators. |
 |
The first natural mode of oscillation occurs at a frequency of ω=0.765 (s/m)1/2. At this requency, all three masses move together in the same direction with the center mass moving 1.414 times farther than the two outer masses. |
 |
The second natural mode of oscillation occurs at a frequency of ω=(2s/m)1/2. At this requency, the center mass does not move (this is a node) while the two outer masses move with the same amplitude but in opposite directions. |
 |
In the third natural mode, the outer two masses move in the same direction with the same amplitude while the center mass moves in the opposite direction with 1.414 times larger amplidue. This mode occurs at a frequency of ω=1.868 (s/m)1/2. |