Vibrational Modes of a Baseball Bat

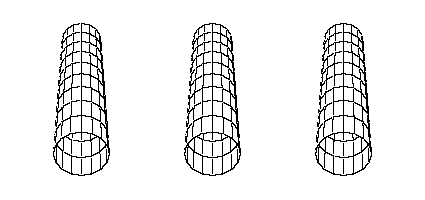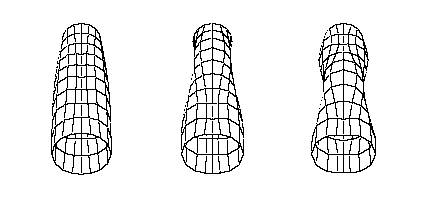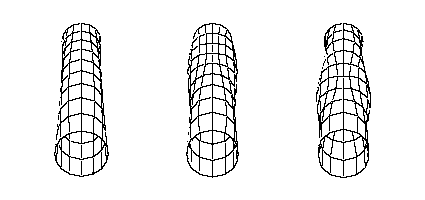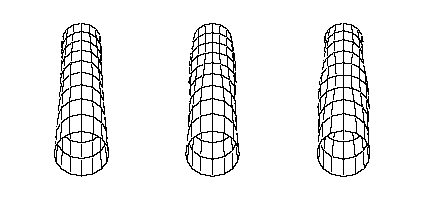
The animations at right show the first four bending modes of a baseball bat. Actually the animations were created from experimental data obtained for a Louisville Slugger Genesis slow pitch softball bat, a hollow barrel bat made from carbon fiber composite materials. However, the vibrational shapes and the node locations are very similar to those for solid wood and aluminum baseball/softball bats I have tested in the acoustics laboratory at Kettering University.

The first bending mode usually occurs at a frequency around 170Hz and is extremely important to the performance of a bat. One of the definitions of the "sweet spot" is the location of the node at the barrel end of the bat. This point, usually 5-7 inches from the barrel end, does not move when the bat is vibrating in its first (or fundamental) bending mode. Another node exists about 6 inches from the handle end (both nodes are identified by the black dots in the animation). An impact at the node will not cause the bat to vibrate, and thus none of the initial energy of the ball will be lost to the bat. In addition, the player will not feel any vibration at this frequency.

The second bending mode, usually occuring near 600Hz, is also very important as it also has a node about 2-3 inches from that of the first bending mode. A "sweet zone" is often defined as the region between the nodes of the first two bending modes.^[2] An impact in region will minimally exite the first two bending modes, so the player will feel little vibration and the ball will not lose energy to bat vibration.

The higher bending modes probably have little influence on the feel of the bat, but computer calculations have shown that they can significantly influence the post-impact ball speed.^[3,4]

The first hoop mode is responsible for both the "trampoline effect" and the "ping" sound of an aluminum bat. For most single walled aluminum bats this mode has a frequency around 2000Hz; for most double walled aluminum bats it is around 1500Hz; and for some recent composite bats it is as low as 1000Hz. This vibrational shape radiates sound in a quadrupole pattern - quadrupoles are rather inefficient sound radiators, but the frequency (2000Hz) is in the range of sounds most readily heard by the human ear so the "ping" can sound quite loud. In well designed bats this first hoop mode shapes is as wide (long) as possible and the location of maximum displacement corresponds to the node of the first bending mode (indicated by the red dot). A ball impact at the sweet spot will excite the hoop mode but not the bending vibrations. Much effort has gone into trying to make the most use of the trampoline effect. My recent research suggests that tuning the first hoop mode to a specific frequency may greatly enhance the trampoline effect and the resulting ball speed.

The second hoop mode is of less importance, and will be minimally excited by a hit near the sweet spot since there is a node (a circle around the circumference of the bat which does not vibrate) there. This mode is an extremely inefficient octupole type of sound radiator and will not be very audible even if exited by a hit off the sweet spot. The third hoop mode is even less important to the performance of a bat.