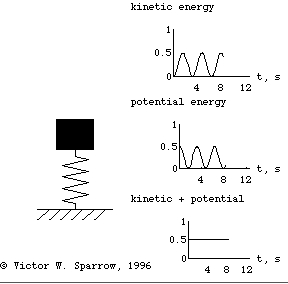
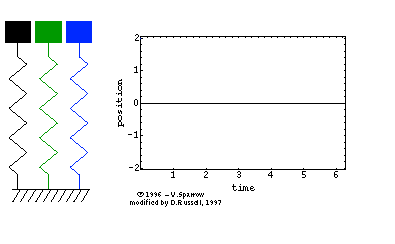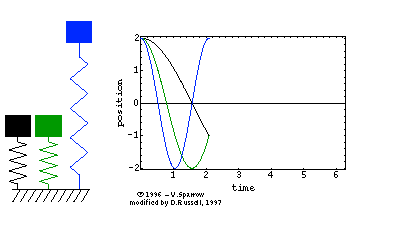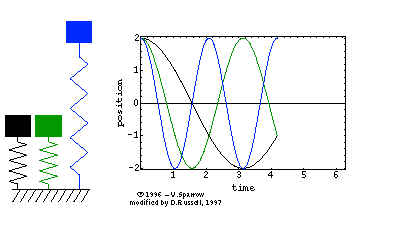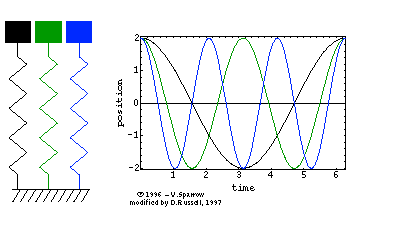
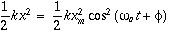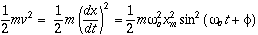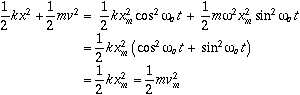 The animated gif at right (click here for mpeg movie) shows the simple harmonic motion of three undamped mass-spring systems, with natural frequencies (from left to right) of ωo, 2ωo, and 3ωo. All three systems are initially at rest, but displaced a distance xm from equilibrium. The animated gif at right (click here for mpeg movie) shows the simple harmonic motion of three undamped mass-spring systems, with natural frequencies (from left to right) of ωo, 2ωo, and 3ωo. All three systems are initially at rest, but displaced a distance xm from equilibrium.
The period of the oscillatory motion is defined as the time required for the system to start one position, complete a cycle of motion and return to the starting position.
⇒ From the position versus time plot, can you determine the period for each of the three oscillators?
|


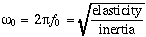
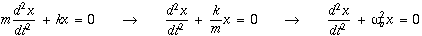
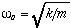 is the natural oscillating frequency. The solutions to this equation of motion takes the form
is the natural oscillating frequency. The solutions to this equation of motion takes the form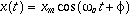
 The animated gif at right (click here for
The animated gif at right (click here for