Refraction of Sound Waves
My Experience with Refracting Sound Waves
I have friends who have a cabin on Island Lake, just north of Park Rapids, MN, and for several years my family used to spend a week each summer at their cabin. The cabin is located at the "X" on the map below, just below the Vacationaire Resort. Approximately 1/3-mile across the lake (indicated by the red ovals in the map and photo below) are several cabins close to the beach and the water. During the daytime we could see people at those cabins across the lake from our dock but we could not hear them. At night, however, we could both see the campers on the other side of the lake and we could also hear and understand their conversations from our dock as they talked around their camp fire. This phenomena is due to the refraction of sound waves due to variations in the speed of sound as a function of temperature near the lake surface.
What is Refraction?
What does refraction look like?


When a plane wave travels in a medium where the wave speed is constant and uniform, the plane wave travels in a constant direction (left-to-right in the first animation shown at right) without any change.
However, when the wave speed varies with location, the wave front will change direction. The second animation, at farthest right, shows a case where the wave speed is faster at the bottom of the region and slower at the top. As a result, the bottom of the plane wavefront is moving faster than the top of the wavefront, and the plane wavefront changes direction and starts moving upward at an angle.
Why does refraction happen?
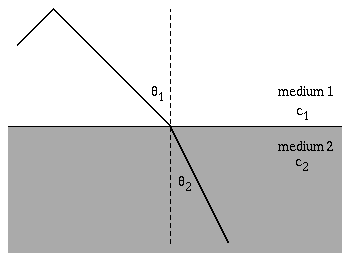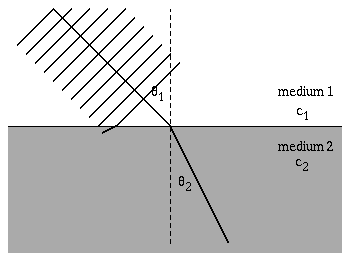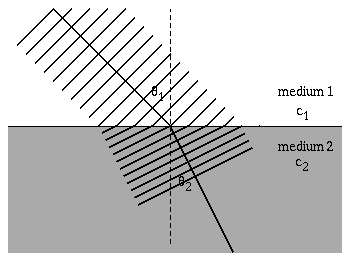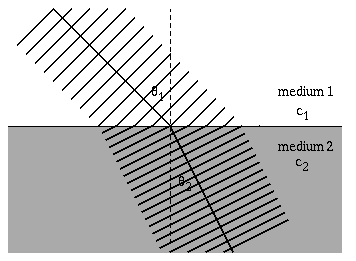
The speed of a wave depends on the elastic and inertia properties of the medium through which it travels. When a wave encounters different medium where the wave speed is different, the wave will change directions. Most often refraction is encountered in a study of optics, with a ray of light incident upon a boundary between two media (air and glass, or air and water, or glass and water). Snell's law relates the directions of the wave before and after it crosses the boundary between the two media. \[ \frac{\sin\theta_1}{c_1} = \frac{\sin\theta_2}{c_2} \] Notice that as the wavefronts cross the boundary the wavelength changes, but the frequency remains constant.
Temperature Lapses and Inversions and the Speed of Sound
In acoustics, however, sound waves usually don't encounter an abrupt change in medium properties. Instead the wave speed changes gradually over a given distance. The speed of a sound wave in air depends on the temperature as \[ c = 331.36 + 0.6067 T \] where \( T \) is the temperature in °C.
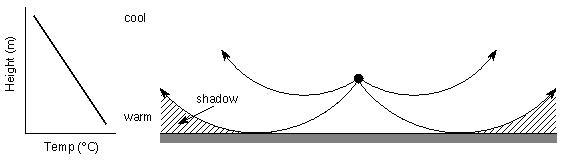
Often the change in the wave speed, and the resulting refraction, is due to a change in the local temperature of the air. For example, during the day the air is warmest right next to the ground and grows cooler above the ground. This is called a temperature lapse. Since the temperature decreases with height, the speed of sound also decreases with height. This means that for a sound wave traveling close to the ground, the part of the wave closest to the ground is traveling the fastest, and the part of the wave farthest above the ground is traveling the slowest. As a result, the wave changes direction and bends upwards. This can create a "shadow zone" region into which the sound wave cannot penetrate. A person standing in the shadow zone will not hear the sound even though he/she might be able to see the source. The sound waves are being refracted upwards and will never reach the observer.
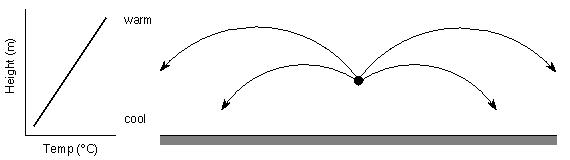
The opposite effect, a temperature inversion occurs when the temperature is coolest right next to the ground and warmer as you increase in height above the ground. Since the temperature increases with height, the speed of sound also increases with height. This means that for a sound wave traveling close to the ground, the part of the wave closest to the ground is traveling the slowest, and the part of the wave farthest above the ground is traveling the fastest. As a result, the wave changes direction and bends downwards. Temperature inversions most often happen at night after the sun goes down when the ground (or water in a lake) cools off quickly, while the air above the ground remains warm. This downward refraction of sound is why you can hear the conversations of campers across the lake, when otherwise you should not be able to hear them. (remember that they can probably hear you too!)
The three animations below compare what happens to a spherical wave pulse if the wave speed depends on position. In the left animation, the wave speed is the same everywhere (a uniform medium) so the wave expands in all directions at the same rate and the spherical wavefront expands as a sphere. In the middle animation, the wave speed is a linear function in the vertical direction, with the speed being faster at the bottom and slower at the top. This could represent a temperature lapse and the result is that the part of the wavefront which was directed downward are refracted so they end up curving upward. In the animation on the right, the wave speed is faster at the top and slower at the bottom, similar to a temperature inversion. Now, the part of the wavefront initially directed upward ends up curving downward.



Refraction of Sound During the Civil War
Acoustician Charles D. Ross has found that refraction of sound caused by temperature and wind gradients may have had a significant impact on the outcome of several Civil War Battles (Gettysburg, Gaines Mill, Fort Donelson, Seven Pines/Fair Oaks, Iuka, Perryville, Chancellorsville, and Five Forks). A summary of his findings are summarized in Echoes, the newsletter of the Acoustical Society of America, and a longer length paper "Outdoor sound propagation in the US Civil War" published in Applied Acoustics. If you are really interested in more, he published a fascinating little book Civil War Acoustic Shadows which describes in detail how acoustics and sound refraction (among other phenomena) could have affected the outcomes of several important battles of the Civil War.


