Physics and Acoustics of Baseball & Softball Bats
Daniel A. Russell, Ph.D.
Graduate Program in Acoustics
The Pennsylvania State University
The contents of this page are ©2003-2011 Daniel A. Russell

Today is The contents of this page were last modified on July 8, 2008
This document, as are all of the articles on my website, is an evolving document. I will continue to modify this document as necessary to correct mistakes, when I think of better ways to explain something, or when I think of new things to add.

Explaining the BESR Performance Standard for NCAA Baseball Bats

In order for non-wood baseball bats to be eligible for use in high school and college NCAA play, they must be

. As I explained in my introductory article about bat performance, Batted-Ball Speed (BBS) is the ultimate performance criteria for bats as they are used in the field. In another article I discussed how the ASA regulates Batted-Ball Speed (BBS) for slow-pitch softball bats directly by measuring the efficiency of the bat-ball collision in the laboratory, and then using field measurements of ball pitch speeds and bat swing speeds - as dependent on moment-of-inertia - to directly predict batted-ball speeds in the field. In this article I'll discuss the approach taken by the NCAA for college baseball and the NFHS for high school baseball, which is to regulate the Batted-Ball Speeds of baseball bats indirectly by regulating the Ball Exit Speed Ratio (BESR) and controlling the bat swing speed by limiting the moment-of-inertia (MOI) of non-wood baseball bats.

Right up front I want to make something clear: The NCAA BESR bat performance standard does NOT regulate the maximum batted-ball speed for a bat. In fact, the BESR standard does not even measure batted-ball speed at all. And, for that matter, it doesn't measure the ball exit speed either. What the standard does measure is the ratio of the ball exit speed to the combined speeds of the pitched ball and swung bat. Knowledge of the Ball-Exit-Speed-Ratio along with the Moment-Of-Inertia of the bat can be used to calculate the batted-ball speed. In fact, the 97-mph hit ball speed usually associated with the BESR standard is a calculation based on a measured BESR for a specific 34-inch wood bat, an assumed bat swing speed of 66-mph and an assumed pitched-ball speed of 70-mph. It may be a representative BBS value for wood bats, but this 97-mph value does not represent the maximum hit-ball speed for a wood bat. In order to leave most MLB ballparks, a baseball has to be hit at speeds around 110-mph, something that MLB players do with wood bats rather frequently. In the only field study of wood and aluminum bats to date, a wood bat was found to hit balls with a maximum batted-ball speed of 101-mph, and an average batted-ball speed of 91.4-mph. The calculated value of the batted-ball speed, calculated from the laboratory measurement of BESR and MOI, for this same bat was 95.0-mph, which is 6-mph lower than the maximum batted-ball speed measured in the field study.

The Physics Equations Behind the BESR Standard

The speed a baseball has after being hit by a baseball bat, termed the Batted-Ball Speed (BBS), is the most obvious and accurate assessment of bat performance in the field of play. The BBS (along with the launch angle, ball spin, and aerodynamic drag forces) is what determines how far a hit ball will travel. Starting with basic physics conservation laws (conservation of linear and angular momentum, conservation of energy, and the definition of coefficient-of-restitution) it is possible to derive an equation for the batted-ball speed as:^[1,2]

(1) where v_ball is the pitched-speed of the ball, v_bat is the linear speed of the bat at the location of impact, e_A is the collision efficiency, a quantity that depends on the elastic properties of both the bat and ball, as well as on the moment-of-inertia of the bat, and the location of the impact on the bat barrel. Back in 1999, when the NCAA was developing their bat performance standard, they defined a term called the Ball-Exit-Speed-Ratio to be equal to the collision efficiency plus a constant

(2) The Batted-Ball Speed in equation (1) may then be written in terms of the BESR as

(3) The BESR (equivalent to the collision efficiency) is the quantity that is measured in the laboratory. For the laboratory test we'll substitute v_exit (the final exit speed of the ball after it collides with the bat) for BBS and rearrange equation (3) to solve for the BESR as^[3]

(4) The original definition of the BESR was designed to take advantage of a laboratory test method (I'll describe it later below) where the initial speeds of the ball and bat before the collision are nearly identical. If v_ball = v_bat then equation (4) reduces to

(5) which may be interpreted as the ratio of the speed with which the ball exits the collision divided by the combined speeds of the bat and ball before the collision. Thus, the name Ball-Exit-Speed-Ratio.^[4] The method of measuring the BESR is relatively simple. You design a device that swings a bat at a moving ball (so that bat speed and ball speed are the same right before impact), measure the speeds of bat and ball prior to the collision, then measure the speed with which the ball leaves the bat, and compute the ratio from equation (5). Once the BESR is known, it is possible to calculate a prediction of the batted-ball speed (BBS) for a bat in the field by simply plugging in the laboratory value for the BESR into equation (3) along with a value for the pitched ball speed v_ball and the bat swing speed v_bat.

The interpretation of the Batted-Ball Speed equation (3) means that a larger BESR will produce a larger BBS, assuming ball and bat speeds don't change. Faster bat speeds also result in faster batted-ball speeds, with a change in bat speed having a greater effect on the BBS than a similar change in pitched-ball speed. This last fact is very important. Consider two bats that have the same BESR as measured in the lab, but which can be swung with significantly different speeds. The bat which can be swung faster will produce a higher batted-ball speed in the field if the BESR value is the same for both bats. The one important factor that BESR cannot measure is the manner in which bat weight and moment-of-inertia affect bat speed.

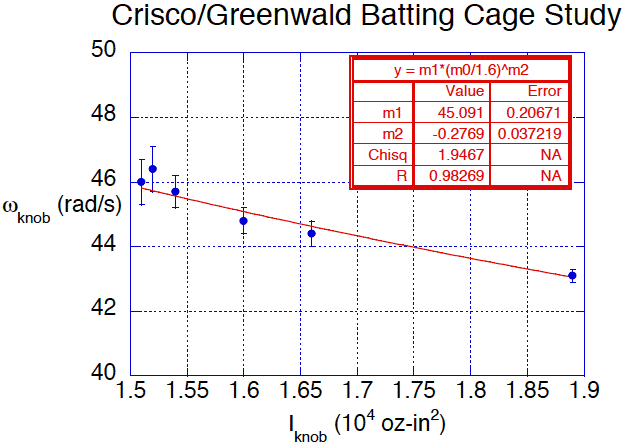The Dependence of Swing Speed on Moment-of-Inertia for Baseball Bats

In 2000 it became apparent that the BESR standard alone cannot account for variations in bat speed in the field. So, the NCAA also decided to regulate the minimum weight and moment-of-inertia (MOI) a non-wood bat can have. This decision is based on field studies which show a direct correlation between the speed with which a baseball bat can be swung and the moment-of-inertia of the bat. Three field studies in particular have focused on the relationship between bat speed an moment-of-inertia for adult baseball bats,^[5-7] and all three studies concluded that bat speed is higher for bats with lower moments-of-inertia and lower for bats with larger moments-of-inertia. Alan Nathan has analyzed the bat swing speed data from the Fleisig^[5] and Crisco-Greenwald^[7] field studies and has fit the data with formulas that can be used to calculate bat speed. The graph at right shows the data and the fit for the Crisco-Greenwald data, and the resulting equation relating the angular velocity of the bat about a pivot point at the knob varies with the moment-of-inertia about the knob (I_knob) is

For the Fleisig field study, Nathan's fit to the data is

We have to do a couple of things to either of these equations before have the value of bat speed necessary for predicting BBS. First we must convert angular velocity to linear speed at the impact point. Assuming an impact at the sweet spot 6-inches from the barrel end of the bat (or 28-inches from the knob), we can simply multiply the angular velocity by 28-inches to obtain the linear velocity at the sweet spot. This gives a resulting bat speed at the impact location with units of inches per second. If we multiply this value by 0.05682 we obtain the bat swing speed in miles per hour. The more tricky conversion we might also have to do involves the value of I_knob. The moment-of-inertia of a bat is usually measured with respect to a pivot point on the handle, 6-inches from the knob. But, the swing speed equations use the moment-of-inertia about a pivot point at the knob. If you know the mass of the bat and the balance point (location of center-of-gravity), you can use the parallel axis theorem to calculate I_knob from the MOI at the 6-inch point. For the bats used in the Crisco-Greenwald batting cage study, the conversion is roughly I_knob = 1.493*MOI₆ + 1610 with units of oz-in².

As an example, a typical 34" wood bat has a moment of inertia of 11,500 oz-in² measured with respect to a pivot at the 6-inch point on the handle. The linear bat speed at the sweet spot is then calculated to be: Crisco-Greenwald v_bat = 68.6 mph and Fleisig v_bat = 59.3 mph. For the calculations I describe below, I used an average of the two bat-swing equations.

Conceptual Explanation of the NCAA Approach to Regulating Bat Performance

Batted-Ball Speed (BBS) is the ultimate performance criteria, and it depends on the speed of the pitched ball, the BESR and the bat swing speed. The NCAA and NFHS regulate the BESR directly - by measuring it in a laboratory - and regulate bat swing speed indirectly by placing a lower limit on the MOI a bat can have. The question is, how do the BESR and MOI influence BBS, and can we understand what the regulations mean about bat performance without having to discuss physics equations? Well, let's review what we know about Batted-Ball Speed. Assuming all other things remain the same:

Faster pitched-ball speeds result in higher BBS. The BESR test is conducted with an assumed pitched-ball speed of 70-mph.
A more effective collision between bat and ball results in a higher value of the BESR which increases BBS.
Bat swing speed depends on the moment-of-inertia (MOI) of a bat, with larger MOI bats being more difficult to swing quickly. Lower bat speed, due to larger MOI, lowers BBS. Higher bat speed, due to lower MOI, will raise BBS.

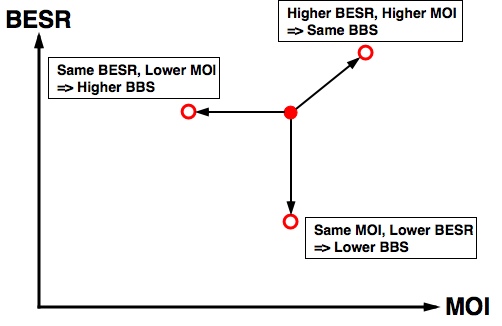
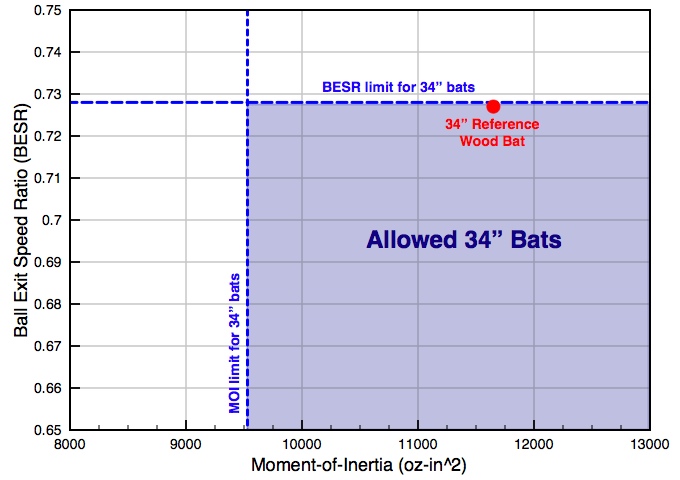
So, let's explore graphically how we would expect changes in BESR or MOI to affect BBS. The graphical approach below should greatly aid in understanding the performance standard. I would like to be able to claim this graphical approach as my own invention - but I will readily admit that I adapted it from a presentation by Dr. Alan Nathan (Univ. of Ill).

The graphic shows a plot of BESR versus MOI which are the two quantities the NCAA regulates for high school and college baseball bats. The solid red dot represents a particular bat with a certain BESR and MOI. First, let's see what happens of the BESR is held constant, but the MOI is lowered. Since the BESR is the same, the collision efficiency is also the same. But, since the MOI is lower, the bat can be swung faster which means that the Batted-Ball Speed will increase. Data points on the left of our graph will have higher Batted-Ball Speeds than data points on the right side off the graph.
As a second case, let's keep the MOI constant, but lower the BESR. Now the swing speed will remain constant (same MOI) but the collision efficiency will decrease due to the lower BESR. This will result in a lower BBS. Data points at the bottom of the graph will have lower Batted-Ball Speeds than data points at the top of the graph.
And finally, if we increase the BESR and the MOI at the same time, then the collision efficiency will increase, the but bat speed will decrease. If the increase in BESR and the decrease in bat speed offset each other, then the Batted-Ball Speed will not change.

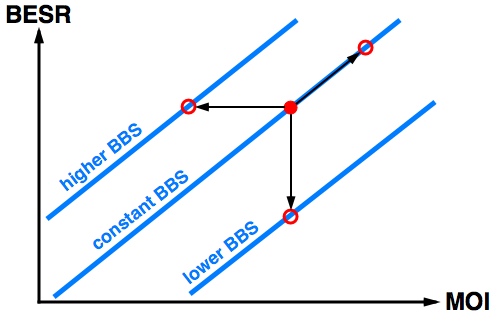
This result implies that we could draw some diagonal lines that represent constant BBS contour lines on our graph of BESR versus MOI. If the BESR and MOI change together so as to offset each other, then the location of our red dot simply moves back and forth diagonally along a constant BBS contour line. The Batted-Ball Speed would be the same for any combination of BESR and MOI that fall on the same contour line. But, if we change the BESR and MOI values in different amounts (or keep one the same while we change the other) then we jump to another contour line which could have a higher or lower value for Batted-Ball Speed.
The reason that a constant BBS contour lines exist is due to a subtle fact that the BESR itself depends on the MOI of the bat. A lower MOI bat has less effective collision with a ball, resulting in a lower value of the BESR. A bat with a larger MOI has a more effective collision with the ball and the resulting BESR is higher. So, while a lower MOI bat can be swung faster, the lower MOI renders the collision less effective. It is a relatively easy calculation to show that the two effects (higher bat speed versus lower BESR) almost exactly cancel each other so that if the elastic properties of the barrel are kept constant, changing the MOI ends up having very little effect on the final Batted-Ball Speed. This is precisely the reason that corked wood bats don't actually offer any real advantage to a player trying to hit a home run - the increased swing speed to due the lower MOI is offset by a less effective collision between bat and ball (corking a wood bat changes the elastic properties of the bat by a negligible amount). Experimental data for the six bats in the Brown University batting cage study^[7] show the same result. The variation in measured bat-swing speeds due variations in bat MOI was almost completely offset by a decrease in the measured value of the BESR so that the differences in performance can be entirely explained by differences in the elastic properties of the barrel (i.e., the trampoline effect).

Now let's take the concepts of the BESR, MOI, and constant BBS contour lines and see if we can understand how the NCAA uses them to regulate the performance of non-wood baseball bats. In 1999 the NCAA tested a 34-inch pro-stock wood bat and found that it produced a BESR of 0.728 in a test apparatus that used a ball speed of 70-mph and a bat swing speed of 66-mph. This BESR value was set as the upper limit for any 34-inch bat, wood, aluminum, or composite. However, since the BESR standard does not account for swing speed (which depends on MOI), the NCAA also regulates the weight and MOI for non-wood bats. 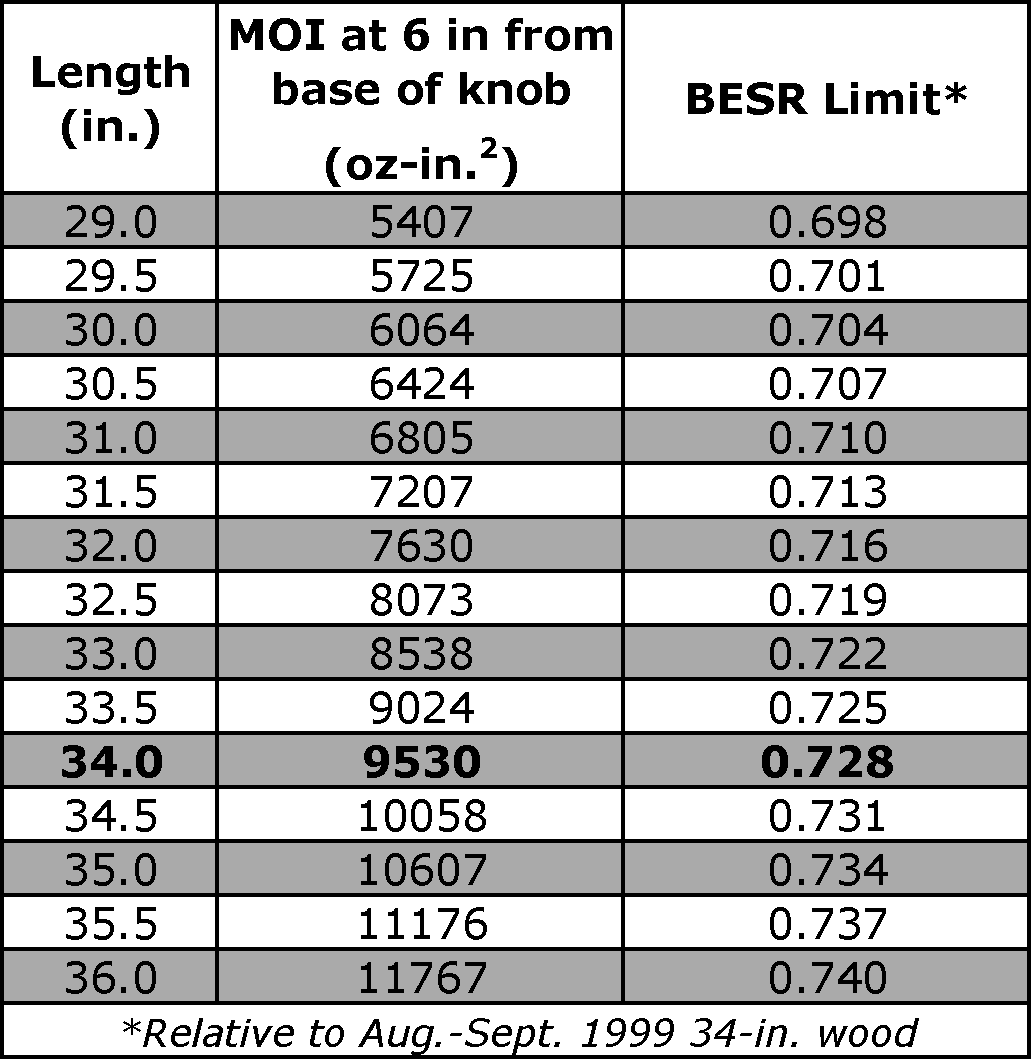The NCAA has decided that a non-wood 34-inch baseball bat must have a weight of at least 31-oz, and must have a MOI greater than 9530 oz-in², as indicated by the blue shaded region on the graph. The NCAA also tested the BESR for a 33-inch and 32-inch wood bat and used the results to extrapolate a sliding scale (shown at left) of BESR and MOI limits for bats of any length.
It should be noted, again, that the NCAA bat performance standard does not regulate batted-ball speed. Instead, it requires that non-wood bats have a ball-exit-speed-ratio (BESR) equal to or less than the value for a high quality wood bat of the same length. And, the moment-of-inertia of the non-wood bat must be greater than some lower limit.

Now, If I take the BESR and MOI values for the 34-inch reference wood bat, assume a pitched-ball speed of 70-mph and use the bat-swing formulas to calculate bat speed for an impact at the sweet spot of a 34-inch bat of a given MOI, then I obtain a calculated value of the batted-ball speed to be 97-mph for this 34" wood bat. This 97-mph BBS does not represent the maximum possible BBS, however. Players who can swing this bat faster will generate higher BBS, as can easily be verified with the BBS equation (3) above. In the hands of a good MLB player, this bat could easily hit balls in excess of 115-mph. I can use the BESR and MOI for this reference bat to determine the Bat-Ball-Coefficient-of-Restitution, or BBCOR which describes the elastic properties of the bat-ball collision. Keeping this elastic property constant, I can change the MOI, recalculate the BESR and construct a constant 97-mph contour line as shown on the graph at right. Notice that there is a triangular section above and to the left of the 97-mph contour line representing allowable non-wood bats that will have Batted-Ball Speeds higher than 97-mph.
If I use the bat-swing formulas to calculate bat-swing speed for a bat with BESR=0.728 and MOI-9530 oz-in² (at the upper left hand corner of the blue shaded region), I find that it is possible for a bat to produce a batted-ball speed of 102-mph and still fall within the NCAA BESR and MOI limits. This does not mean that every NCAA approved non-wood bat hits balls 5-mph faster than wood bats. I do not know how many (if any) NCAA approved non-wood bats come close to this BBS value - that data is not in the public domain.(See update at right) However, the performance standard currently used by the NCAA and NFHS to regulate baseball bat performance clearly allows for non-wood bats to hit balls up to 5-mph faster than the high quality wood reference bat.
This 5-mph potential advantage for non-wood bats would appear to contradict the claims of some groups (like the Don't Take My Bat Away! Coalition) who have repeatedly gone on record claiming that today's legal metal bats generate batted-ball speeds exactly the same as wood. However, the allowance for a 5-mph advantage for non-wood bats is fact - built into the BESR+MOI standard, and backed up by experimental data. Moreover, the NCAA is aware of this possible 5-mph metal bat advantage, and they are quite happy with the current state of college baseball. For the sake of argument, though, if the NCAA wanted to regulate bat performance so that non-wood bats would hit balls with exactly the same speed as wood bats using the BESR+MOI performance standard then they would have to either^[8]

require the MOI limit for a non-wood bat to be equal to the MOI value of a typical wood bat.
use a sliding scale that adjusts the maximum BESR to vary with MOI to follow the 97-mph constant BBS contour
I would like to point out that a difference of 5-mph is far short of the supposed (and erroneous) 20 to 30-mph advantage of non-wood bats that has been recently printed in several newspapers and that has been used to argue for the banning of non-wood bats in recent legislative hearings in New York City, New Jersey, Wyoming, Pennsylvania, and Illinois because of supposed safety concerns. I have a separate article that tackles the question of banning metal bats and safety and it is my scientific opinion that a 5-mph advantage for metal bats does not pose a increased safety risk to baseball players. Since the NCAA began regulating bat performance with the BESR and MOI standard in 1999, batting averages and the number of home runs per game have dropped, and the frequency of players being injured by hit balls has also dropped, so the regulation of bat performance using the BESR and MOI standard appears to be working.
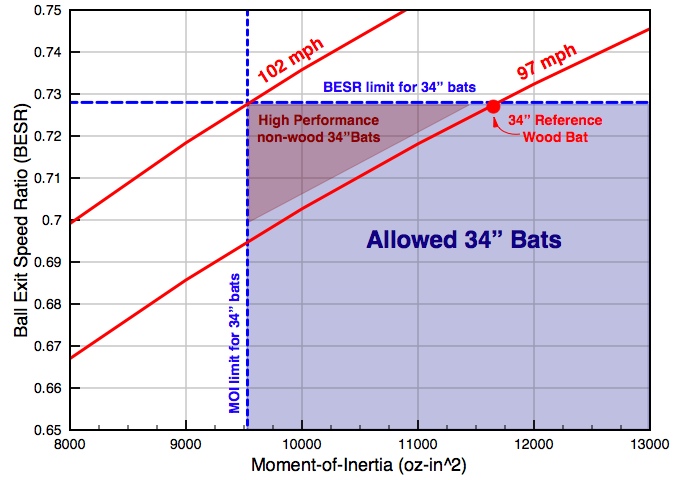
Update: July 8, 2008 I have just seen some proprietary experimental data that is not yet in the public domain, but at the risk of "getting in trouble" I will briefly summarize because it proves that the above charts and interpretations are not just theoretical ideas. Sixteen wood and 72 non-wood (metal and composite) 34-inch baseball bats were recently certified as passing the NCAA BESR+MOI performance standard. The 16 wood bats had laboratory experimental batted-ball speeds ranging from 94-mph to 97.5 mph. The 72 non-wood bats had laboratory experimental batted-ball speeds ranging from 93-mph to 102.5-mph. Both ranges are exactly where the charts above predict them to fall. From this I can draw two conclusions: (1) Some current non-wood bats produce the same batted-ball speeds (or even a little less) than wood. (2) Many current non-wood bats can hit balls up to 5-mph faster than the best wood bats. Both conclusions show that the BESR+MOI standard does exactly what it was designed to do. Furthermore, this range of laboratory data also agrees with the limited experimental data from field tests as I discuss below.

How Accurately does the BESR and MOI Standard Predict Bat Performance in the Field?

One of the problems with trying to understand the BESR standard is that there is almost no data correlating field studies of bat performance to laboratory measurements for the same group of bats. In fact, the only comprehensive field study of baseball bat performance that I am aware of is the Brown University batting cage study conducted by Crisco and Greenwald in 1997.^[7,9-11] This study involved 19 batters (4 high school, 6 college, and 9 minor league pros) swinging one wood bat and five metal bats. Batters were swinging at balls pitched from a pitching machine at speeds between 48-65 mph. The primary goal of this field study was to compare batted-ball speeds as measured in the field with batted-ball speeds predicted from laboratory measurements, and the results showed a very good agreement between laboratory and field data. A second result was that while some metal bats performed statistically the same as wood bats, other metal bats were found to hit balls significantly faster than wood. The results from this study are often used incorrectly to argue against the use of metal bats because of the high batted-ball speeds for some of the metal bats. However, only one of the five metal bats in the Brown University study is legal under the current NCAA bat performance standards.

Dr. Alan Nathan has spent a considerable amount of time analyzing the raw data from this batting cage study and was able to extract Bat-Ball-Coefficients-of-Restitution for each of the 538 impacts recorded. Knowing the BBCOR and MOI of a bat, it is possible to calculate the BESR and make a prediction of Batted-Ball Speed. In the Fall of 2005 Dr. Nathan and I arranged to have the six bats from the Brown University study tested using the ASTM F2219 high speed BESR testing protocol, and the laboratory BESR measurements agreed with the data from the field study almost perfectly. Armed with the BBCOR, BESR and MOI values for the bats we can locate the bats on the BESR-MOI scale, predict the Batted-Ball Speed and compare to the field measurements.

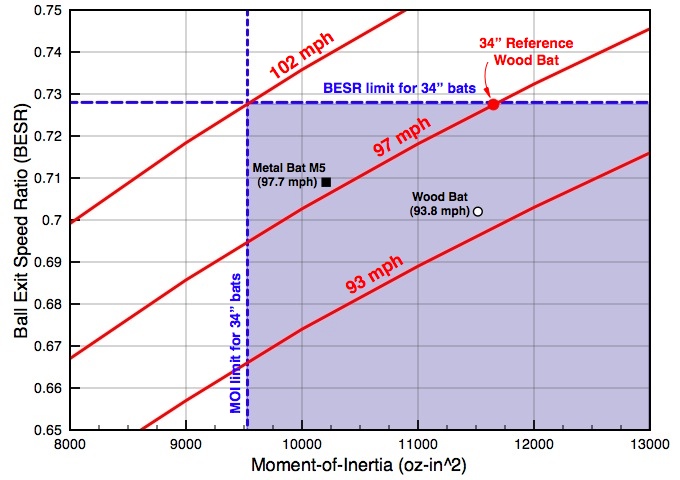
Two of the bats (one wood and one metal) in the Brown University batting cage study were 34" in length, and the other four metal bats were 33" long. The blue shaded graphic at right shows the BESR and MOI limits for 34" bats along with constant BBS contours for 93-mph, 97-mph and 102-mph. The white circle and solid black square data points represent BESR and MOI values for the 34" wood bat and the 34" metal bat M5, respectively, from the Brown University batting cage study. The batted ball speed given in parenthesis is calculated from the BBS equation (3) above using the BESR, MOI, along with the bat-swing speed calculated from the formulas with the bat's MOI, and an assumed pitched-ball speed of 70-mph. The predicted BBS of 93.8-mph for the wood bat from the Brown University study is significantly lower than the 97-mph NCAA reference wood bat used to set the BESR standard, as should be expected since its BESR is much lower. It is interesting to note that the predicted BBS for the 34" metal bat from the Brown University study is only 0.7-mph faster than the predicted 97 mph BBS for the NCAA 34" reference wood bat. This 34" metal bat would not be legal today, however, because it weighs 30-oz and thus fails the "minus-3" rule.
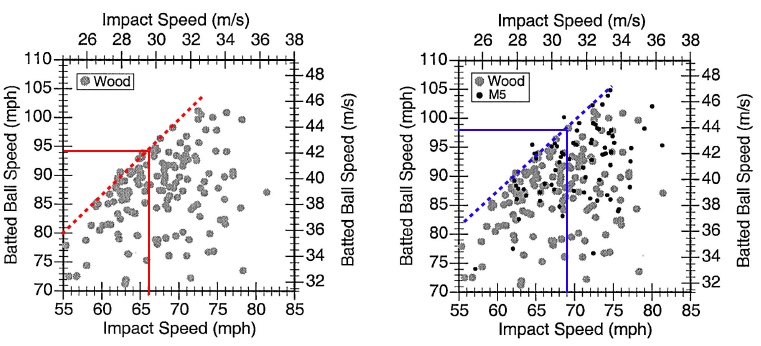
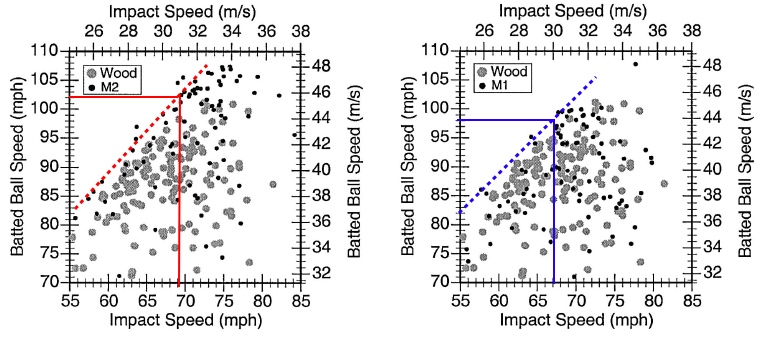
So, how well does the BESR standard predict the field performance of bats? Pretty well actually - as long as you remember that the BESR standard assumes a pitched-ball speed of 70-mph and a bat-swig speed of 66-mph. The scatter plots at right show the measured Batted-Ball Speeds as a function of bat-swing speed (impact speed on the plots) for the 34" wood bat and 34" metal bat M5 from the Brown University study.^[10] Using the bat-swing speed formulas (discussed above) and the MOI values of the bats, the swing speeds are calculated to be 66-mph and 69-mph for the wood and metal bats respectively. Looking at the left scatter plot for the wood bat, a bat-swing speed of 66-mph corresponds to a maximum BBS of 94-mph. Using the measured BESR and MOI for this wood bat, I calculated a BBS of 93.8-mph. Looking at the right scatter plot for metal bat M5, a bat-swing speed of 69-mph corresponds to a maximum BBS of 98-mph. Using the the measured BESR and MOI for this metal bat, I calculated a BBS of 97.7-mph. I would say the BESR and MOI values and the BBS equation allows fora pretty accurate prediction of the maximum batted-ball speed in the field for a given swing speed.
After comparing the BESR-MOI graphic and the BBS-vs-Bat Speed scatter plots, two important observations stand out to me:

Batted-Ball speed depends on the bat-swing speed. The scatter plots clearly show that the maximum measured BBS increases as the bat-swing speed increases. The bat-swing speed calculated from the formulas apparently represents the "average" bat-swing speed that a typical player might achieve. But the data clearly shows, and the BBS equation agrees, that players who can swing a bat faster can hit balls faster with that bat.
The BBS predicted from the BESR, MOI and bat-speed does not represent the maximum possible BBS for a given bat. The predicted BBS for the wood bat was 94-mph, while the maximum BBS (corresponding to a higher bat speed) for the wood bat was 101-mph. The predicted BBS for the metal bat was 98-mph while the maximum BBS was 105-mph.

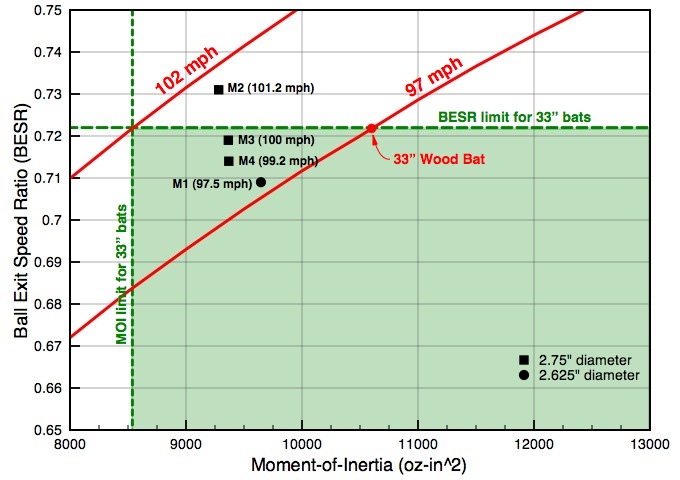
The other four metal bats from the Brown University field study were 33" in length. The green shaded area in the graphic at right shows the BESR and MOI limits for 33" bats along with constant BBS contours corresponding to 97-mph and 102-mph. I've also plotted the BESR and MOI data point for a high quality 33" wood bat, which has the maximum allowed BESR and has a swing speed of 66-mph so that the Batted-Ball speed (assuming a pitched-ball speed of 70-mph) is right about 97-mph. Notice that the maximum allowed BBS for a non-wood bat that falls within the BESR and MOI limits is 102-mph, exactly the same as was the case for 34" bats. The black square and circle data points represent the predicted Batted-Ball Speeds (calculated from experimental values of BESR and MOI) for the four 33" metal bats from the Brown University study. Notice that the highest performing bat from the Brown University study exceeds the BESR limit and so would not be legal today. Three of these 33" metal bats (square data points) also have a barrel diameter of 2.75" which is larger than the 2.625" diameter limit adopted by the NCAA in 1999, and they also fail to meet the "minus 3" rule (one is -4 and two are -5), and so none of these three bats would be legal under the current NCAA performance standards. In fact, of the five metal bats field tested in the Brown University study only one would be legal under the current NCAA performance standards - the bat indicated by the solid black circle. This legal metal bat has a predicted BBS only 0.5-higher than the "wood-bat" standard.
How well do these BBS predictions match field measurements? The scatter plots below right show the measured field data for the highest performing metal bat M2 and the legal metal bat M1. Using MOI for bat M2, the swing-speed formulas give a typical swing speed of 69-mph. The scatter plot shows that a bat-swing speed of 69-mph corresponds to a maximum measured BBS of about 102-mph. This agrees rather well with the 101.2-mph prediction. For the other metal bat, M1, the MOI and swing speed formulas give a swing speed of about 67-mph which corresponds to a predicted BBS of 98-mph. This agrees with the predicted value of 97.5-mph. As was the case for the 34" bats, the predicted BBS values - which are based on a typical swing speed - do not represent the maximum possible Batted-Ball Speeds (107-mph for M2 and 99-mph for M1). Players who can swing the bats faster can generate faster Batted-Ball Speeds.
I can draw several conclusions from this analysis of the NCAA BESR and MOI bat performance standard:

The current NCAA BESR and MOI standard allows non-wood bats to produce Batted-Ball Speeds approximately 5-mph faster than a high quality wood bat of the same length.
Predictions of Batted-Ball Speeds obtained by using measured BESR and MOI values in the BBS equation agree very well with measured values (for the same bat-swing speeds) from the Brown University field study.
Predicted BBS values do not represent the maximum possible Batted-Ball Speeds for any bat, wood, metal or composite. Players who can swing a given bat faster will generate higher Batted-Ball Speeds than a typical player.
Even for the supposedly "extremely high performing" metal bats from the Brown University study, the predicted Batted-Ball Speeds are not excessively faster than those for a wood bat.

How is the BESR Measured in the Laboratory?

After the 1998 season the NCAA developed the BESR test to measure and limit baseball bat performance. The NCAA began requiring bats to be performance tested during the 2000 season. The effect that these performance standards have had on the game of collegiate baseball is evident when one tracks the batting and home run statistics. Every single baseball bat approved for play at the high-school, NCAA college, and Major League Baseball levels is tested at the Baseball Research Center run by Jim Sherwood at the University of Massachusetts Lowell. Once the bat has passed the BESR test in the laboratory, and provided it has an acceptable MOI, the bat model is cleared to bear the "BESR Certified" stamp on the barrel.

Old BESR Testing Protocol (pre-2006)

The BESR standard, and the definition of the BESR itself, were defined with reference to a specific test apparatus that rotates a bat gripped at the handle to impact a moving ball. The rotational speed of the bat and the speed of the ball can be controlled by the operator. According to the original NCAA Certification Protocol^[12] established in 1999, this method was used to test bats between 32" and 35" in length. The bat is mounted onto a rotating axis by a grip centered at 5-7/16" from the end of the knob. The bat is rotated so that a point on the barrel 6-inches from the end of the bat is traveling at a linear speed of 66±1 mph when it impacts the ball which is moving towards the bat with a linear speed of 70±2 mph. This means that the combined relative speed between bat and ball is 136 mph at the moment of impact. The ball exit speed is measured with a set of light speed-gates and the ball is required to pass through the small diamond shaped hole in the wall (shown in the photo) in order to be counted as a valid hit. The BESR is first measured at the 6-inch point on the barrel, then also at the 5" and 7" points to ensure that the maximum BESR value is found. An average of 5 valid measurements is recorded as the BESR result. The measured BESR value is compared to the maximum value allowed for the specific bat length, and if the measured BESR is below the accepted value the bat is considered to be BESR Certified.

All BESR testing of bats for NCAA college and high school use is conducted in the laboratory at the Baseball Research Center at the University of Massachusetts Lowell. There are only two existing copies of the bat hitting machine used to test bats to the BESR standard - the second copy is in the possession of the guy who invented it (but I'm pretty sure I heard that his hasn't worked in some time). Due to licensing restrictions imposed by the machine's inventor, this device has not been allowed to be used for research purposes. Unfortunately, this means that very little research has been conducted to verify the success of the BESR standard for shorter bats.

Bat hitting machine used to conduct the moving bat moving ball version of the BESR test protocol. Photo courtesy of the UMass-Lowell Baseball Research Center.

Current BESR Testing Protocol (2006-present)

In 2006 the inventor of the bat-ball hitting machine formerly used to conduct the BESR test filed a multi-million dollar lawsuit against the Baseball Research Center and the NCAA for supposedly violating the terms of their license agreement. The NCAA has since abandoned the use of this machine in favor of a high-speed cannon test identical to that used by the Amateur Softball Association to regulate the performance of softball bats.

For this new test standard protocol^[13] (which follows the ASTM standard F2219^[14]) a baseball is fired from a cannon at a speed of 138-mph towards a bat which is initially at rest (v_bat=0), gripped in pivot that is free to rotate after the ball hits the bat. The speeds of the ball as it approaches the bat and as it rebounds from the bat are measured with a series of light gates. The BESR is calculated from equation (5) above with v_bat=0 so that

One of the things that makes this possible is that the BESR (or the equivalent collision efficiency) is independent of the reference frame. The measured exit speed of the ball will depend on whether or not the bat and ball are initially moving or initially stationary but the value of the BESR and e_A will be the same.

This test method and equipment has no restrictions on its use for research purposes. Current testing is underway at the Baseball Research Center in an attempt to investigate the extension of the BESR standard to shorter length youth baseball bats. Unfortunately, one of the problems with this "ball-in, ball-out" method is that bats moments-of-inertia below 7000 oz-in² tend to have extremely low collision efficiency (or BESR) so that they often don't rebound with enough speed to pass through the ball speed gates. A possible fix to this problem is to measure the bat rebound speed after the collision and to use this to determine the BESR.

Ball cannon, light gates, and bat pivot used to conduct the high-speed "ball-in ball-out" version of the BESR test protocol. Photo courtesy of the WSU Sports Science Laboratory..

Schematic of the test apparatus from ASTM F2219.

References

[1] A.M. Nathan, "Dynamics of the bat-ball collision," Am. J. Phys. 68, 979-990 (2000)
[2] A.M. Nathan, "Characterizing the performance of baseball bats," Am. J. Phys. 71(2), 134-143 (2003)
[3] M.M. Carroll, "Assessment and regulation of baseball bat performance," Symposium on Trends in the Application of Mathematics to Mechanics, edited by P.E. O'Donoghue and J.N. Flavin (Elsevier, Amsterdam, 2000), pp. 17-26.
[4] The BESR (Ball Exit Speed Ratio) White Paper by Dr. James Ashton-Miller, Dr. Michael Carroll, Dr. Kenneth Johnson, Dr. Alan Nathan (NCAA Baseball Research Panel) and Todd Petr, Ty Halpin (NCAA)
[5] G. Fleisig, N. Zheng, D. Stodden, and J. Andrews, "Relationship between bat mass properties and bat velocity," Sports Engineering, 5(1), 1-8 (2002).
[6] K. Koenig, N. Mitchel, T. Hannigan, and J. Clutter, "The influence of moment of inertia on baseball/softball bat swing speed," Sports Engineering, 7(2), 105-118 (2004).
[7] R. M. Greenwald, L. H. Penna, and J. J. Crisco, "Differences in Batted-Ball Speed With Wood and Aluminum Baseball Bats: A Batting Cage Study," J. Appl. Biomech., 17, 241-252 (2001).
[8] Alan M. Nathan Some Thoughts on Wood versus Aluminum Bats," submitted to the Massachusetts Interscholastic Athletic Association, (January 10, 2003).
[9] J.J. Crisco and R.W. Greenwald, "Metal baseball bats can outperform wood bats with a similar `sweet spot'," Proceedings of the 24th Annual Meeting, American Society of Biomechanics. Chicago, IL. July 19-22 (2000).
[10] J.J. Crisco, R.M. Greenwald, J.D. Blume, and L.H. Penna, "Batting performance of wood and metal baseball bats," Med. Sci. Sports Exerc., 34(10), 1675-1684 (2002)
[11] J.J. Crisco and R.W. Greenwald, "Batted Ball Speed as a Function of Swing Speed and Impact Location," presented at the 2001 Annual SGMA Baseball/Softball Industry Meeting, Chicago, IL (2001).
[12] NCAA Provisional Standard for Testing Baseball Bat Performance, (September 27, 1999).
[13] NCAA Standard for Testing Baseball Bat Performance, (November 2005, Revised October 2006).
[14] ASTM Standard F2219-05, "Standard Test Methods for Measuring High-Speed Bat Performance," Annual Book of ASTM Standards, (ASTM, 2005).

Back to Physics and Acoustics of Baseball & Softball Bats

hits since May 1, 2007

The graphic shows a plot of BESR versus MOI which are the two quantities the NCAA regulates for high school and college baseball bats. The solid red dot represents a particular bat with a certain BESR and MOI. First, let's see what happens of the BESR is held constant, but the MOI is lowered. Since the BESR is the same, the collision efficiency is also the same. But, since the MOI is lower, the bat can be swung faster which means that the Batted-Ball Speed will increase. Data points on the left of our graph will have higher Batted-Ball Speeds than data points on the right side off the graph. As a second case, let's keep the MOI constant, but lower the BESR. Now the swing speed will remain constant (same MOI) but the collision efficiency will decrease due to the lower BESR. This will result in a lower BBS. Data points at the bottom of the graph will have lower Batted-Ball Speeds than data points at the top of the graph. And finally, if we increase the BESR and the MOI at the same time, then the collision efficiency will increase, the but bat speed will decrease. If the increase in BESR and the decrease in bat speed offset each other, then the Batted-Ball Speed will not change.
This result implies that we could draw some diagonal lines that represent constant BBS contour lines on our graph of BESR versus MOI. If the BESR and MOI change together so as to offset each other, then the location of our red dot simply moves back and forth diagonally along a constant BBS contour line. The Batted-Ball Speed would be the same for any combination of BESR and MOI that fall on the same contour line. But, if we change the BESR and MOI values in different amounts (or keep one the same while we change the other) then we jump to another contour line which could have a higher or lower value for Batted-Ball Speed. The reason that a constant BBS contour lines exist is due to a subtle fact that the BESR itself depends on the MOI of the bat. A lower MOI bat has less effective collision with a ball, resulting in a lower value of the BESR. A bat with a larger MOI has a more effective collision with the ball and the resulting BESR is higher. So, while a lower MOI bat can be swung faster, the lower MOI renders the collision less effective. It is a relatively easy calculation to show that the two effects (higher bat speed versus lower BESR) almost exactly cancel each other so that if the elastic properties of the barrel are kept constant, changing the MOI ends up having very little effect on the final Batted-Ball Speed. This is precisely the reason that corked wood bats don't actually offer any real advantage to a player trying to hit a home run - the increased swing speed to due the lower MOI is offset by a less effective collision between bat and ball (corking a wood bat changes the elastic properties of the bat by a negligible amount). Experimental data for the six bats in the Brown University batting cage study^[7] show the same result. The variation in measured bat-swing speeds due variations in bat MOI was almost completely offset by a decrease in the measured value of the BESR so that the differences in performance can be entirely explained by differences in the elastic properties of the barrel (i.e., the trampoline effect).
Now let's take the concepts of the BESR, MOI, and constant BBS contour lines and see if we can understand how the NCAA uses them to regulate the performance of non-wood baseball bats. In 1999 the NCAA tested a 34-inch pro-stock wood bat and found that it produced a BESR of 0.728 in a test apparatus that used a ball speed of 70-mph and a bat swing speed of 66-mph. This BESR value was set as the upper limit for any 34-inch bat, wood, aluminum, or composite. However, since the BESR standard does not account for swing speed (which depends on MOI), the NCAA also regulates the weight and MOI for non-wood bats. The NCAA has decided that a non-wood 34-inch baseball bat must have a weight of at least 31-oz, and must have a MOI greater than 9530 oz-in², as indicated by the blue shaded region on the graph. The NCAA also tested the BESR for a 33-inch and 32-inch wood bat and used the results to extrapolate a sliding scale (shown at left) of BESR and MOI limits for bats of any length. It should be noted, again, that the NCAA bat performance standard does not regulate batted-ball speed. Instead, it requires that non-wood bats have a ball-exit-speed-ratio (BESR) equal to or less than the value for a high quality wood bat of the same length. And, the moment-of-inertia of the non-wood bat must be greater than some lower limit.
Now, If I take the BESR and MOI values for the 34-inch reference wood bat, assume a pitched-ball speed of 70-mph and use the bat-swing formulas to calculate bat speed for an impact at the sweet spot of a 34-inch bat of a given MOI, then I obtain a calculated value of the batted-ball speed to be 97-mph for this 34" wood bat. This 97-mph BBS does not represent the maximum possible BBS, however. Players who can swing this bat faster will generate higher BBS, as can easily be verified with the BBS equation (3) above. In the hands of a good MLB player, this bat could easily hit balls in excess of 115-mph. I can use the BESR and MOI for this reference bat to determine the Bat-Ball-Coefficient-of-Restitution, or BBCOR which describes the elastic properties of the bat-ball collision. Keeping this elastic property constant, I can change the MOI, recalculate the BESR and construct a constant 97-mph contour line as shown on the graph at right. Notice that there is a triangular section above and to the left of the 97-mph contour line representing allowable non-wood bats that will have Batted-Ball Speeds higher than 97-mph. If I use the bat-swing formulas to calculate bat-swing speed for a bat with BESR=0.728 and MOI-9530 oz-in² (at the upper left hand corner of the blue shaded region), I find that it is possible for a bat to produce a batted-ball speed of 102-mph and still fall within the NCAA BESR and MOI limits. This does not mean that every NCAA approved non-wood bat hits balls 5-mph faster than wood bats. I do not know how many (if any) NCAA approved non-wood bats come close to this BBS value - that data is not in the public domain.(See update at right) However, the performance standard currently used by the NCAA and NFHS to regulate baseball bat performance clearly allows for non-wood bats to hit balls up to 5-mph faster than the high quality wood reference bat. This 5-mph potential advantage for non-wood bats would appear to contradict the claims of some groups (like the Don't Take My Bat Away! Coalition) who have repeatedly gone on record claiming that today's legal metal bats generate batted-ball speeds exactly the same as wood. However, the allowance for a 5-mph advantage for non-wood bats is fact - built into the BESR+MOI standard, and backed up by experimental data. Moreover, the NCAA is aware of this possible 5-mph metal bat advantage, and they are quite happy with the current state of college baseball. For the sake of argument, though, if the NCAA wanted to regulate bat performance so that non-wood bats would hit balls with exactly the same speed as wood bats using the BESR+MOI performance standard then they would have to either^[8] require the MOI limit for a non-wood bat to be equal to the MOI value of a typical wood bat. use a sliding scale that adjusts the maximum BESR to vary with MOI to follow the 97-mph constant BBS contour I would like to point out that a difference of 5-mph is far short of the supposed (and erroneous) 20 to 30-mph advantage of non-wood bats that has been recently printed in several newspapers and that has been used to argue for the banning of non-wood bats in recent legislative hearings in New York City, New Jersey, Wyoming, Pennsylvania, and Illinois because of supposed safety concerns. I have a separate article that tackles the question of banning metal bats and safety and it is my scientific opinion that a 5-mph advantage for metal bats does not pose a increased safety risk to baseball players. Since the NCAA began regulating bat performance with the BESR and MOI standard in 1999, batting averages and the number of home runs per game have dropped, and the frequency of players being injured by hit balls has also dropped, so the regulation of bat performance using the BESR and MOI standard appears to be working.	Update: July 8, 2008 I have just seen some proprietary experimental data that is not yet in the public domain, but at the risk of "getting in trouble" I will briefly summarize because it proves that the above charts and interpretations are not just theoretical ideas. Sixteen wood and 72 non-wood (metal and composite) 34-inch baseball bats were recently certified as passing the NCAA BESR+MOI performance standard. The 16 wood bats had laboratory experimental batted-ball speeds ranging from 94-mph to 97.5 mph. The 72 non-wood bats had laboratory experimental batted-ball speeds ranging from 93-mph to 102.5-mph. Both ranges are exactly where the charts above predict them to fall. From this I can draw two conclusions: (1) Some current non-wood bats produce the same batted-ball speeds (or even a little less) than wood. (2) Many current non-wood bats can hit balls up to 5-mph faster than the best wood bats. Both conclusions show that the BESR+MOI standard does exactly what it was designed to do. Furthermore, this range of laboratory data also agrees with the limited experimental data from field tests as I discuss below.