Modelling the Bat-Ball Collision: Step 1

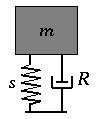
Linear 1-DOF model of the Ball As a first step in an attempt to physically model the bat-ball collision, the ball is modelled as a linear, 1-DOF mass-spring system. The fact that the spring is linear means that the amount of force needed to compress the ball is directly proportional to the resulting amount of compression    F=s x.     The mass and stiffness are taken from data for actual baseballs[1]     m=145.8 g     s=3306.60 N/cm     and the damping factor is estimated from the coefficient of restitution.[2] The coefficient of restitution (COR) is the negative of the ratio of the ball's velocity after impact to its velocity before impact.

Animating the Collision of a Linear Ball with a Rigid Surface

The animation at left was created with Mathematica using the equations of motion for a mass-spring system moving with an initial velocity and impacting a hard rigid surface. The ball essentially acts as a damped harmonic oscillator during the half-cycle of its motion while it is in contact with the surface. In an attempt to make the animation somewhat realistic, I have animated the compression of the spring by the squishing of the outer surface of the ball - the more it squishes, the more the spring compresses. The animation shows three balls with the same initial velocity colliding with a rigid surface. The ball on the left has a damping ratio of 0, resulting in COR=1.0, which means that rebounding velocity is the same as the incoming velocity. While the initial kinetic energy is converted to potential energy during the collision, all of the energy stored in the ball during compression is returned to kinetic energy (elastic collision). The ball in the middle has a damping ratio of 0.25, resulting in COR=0.50, and the rebounding velocity is less than the incoming velocity as some of the ball's initial kinetic energy was lost during the compression/relaxation of the ball. The ball on the right has a damping ratio of 1.0 (critically damped) so that COR=0.0, and does not rebound from the wall at all (perfectly inelastic collision) because all of the incoming kinetic energy was lost during the compression/relaxation of the ball. Notice that the less damping the ball has, the more it is compressed. This works out in the mathematical theory as well as in the (mathematically correct) animations.

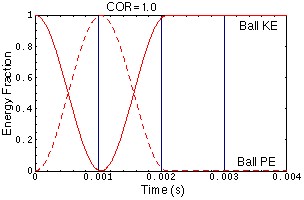
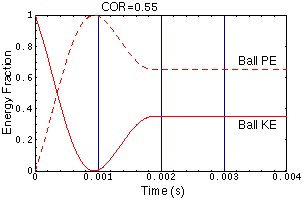
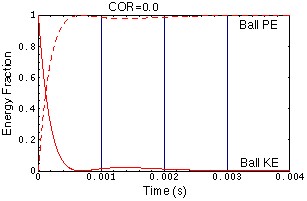
Energy vs Time Curves

Flaws in this Simple Linear Model

Predictions of the linear model which are not true:

• COR does not depend on initial velocity of the ball => Laboratory data shows that COR decreases roughly linearly with increasing impact velocity^[5]
• Contact time does not depend on the initial velocity of the ball => for a nonlinear spring, the contact time decreases with increasing velocity^[6]

References
[1] S. P. Handee, R. M. Greenwald, and J. J. Crisco, "Static and Dynamic Properties of Various Baseballs," Journal of Applied Biomechanics, 14, 390-400 (1998)
[2] P. A. Giacobbe, H. A. Scarton, and Y-S. Lee, "Dynamic Hardness (SDH) of Baseballs and Softballs," International Symposium on Safety in Baseball and Softball, ASTM STP 1313, Earl F. Hoerner and Francis A. Cosgrove, Eds., (American Society for Testing
[3] R. Cross, "Impact of a ball with a bat or racket," American Journal of Physics, 67(8), 692-702 (1999)
[4] R. Cross, "Flexible beam analysis of the effects of string tension and frame stiffness on racket performance," Sports Engineering, 3, 111-122 (2000)
[5] R. Cross, "The bounce of a ball," American Journal of Physics, 67(3), 222-227 (1999)
[6] Unpublished data from high speed camera footage of baseballs colliding with bats made by Biokinetics and Associates Ltd., Ottawa, Ontario, Canada.
[7] D.A. Russell, T.D. Rossing, "Testing piano hammer nonlinearity using residual shock spectra," AcusticaĞacta acustica, 84(5), 967-975 (1998)