Acoustics and Vibration Animations

Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons LicenseThis work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://www.acs.psu.edu/drussell/demos.html. Additional information about using this content is available at http://www.acs.psu.edu/drussell/Demos/copyright.html.

The content of this page was originally posted on May 28, 2008. The HTML code was modified to be HTML5 compliant on March 18, 2013.

Wave Motion in Time and Space

A wave is a disturbance that travels from one location to another, and is described by a wave function that is a function of both space and time. If the wave function was sine function then the wave would be exressed by

$$ \psi(x,t)=A\sin(\omega t \pm kx) $$

where \(A\) is the maximum ampitude of the wave, \(\omega\) is the angular frequency of the wave \(x\) direction and the positive sign is used for a wave traveling in the negative x direction. Note, that the wave function \(\psi\) and the amplitude \(A\) could represent any of a number of quantities which can propagate as waves (i.e., displacement, velocity, pressure, density, temperature, stress, strain, electric and magnetic fields).

The tricky part of understanding wave motion is recognizing the differences between the time and space behavior. Hopefully the animation at left can help. The top part of the animation shows a sine wave pulse traveling from left to right. A red dot has been identified to highlight the time behavior of a point at a specific location.

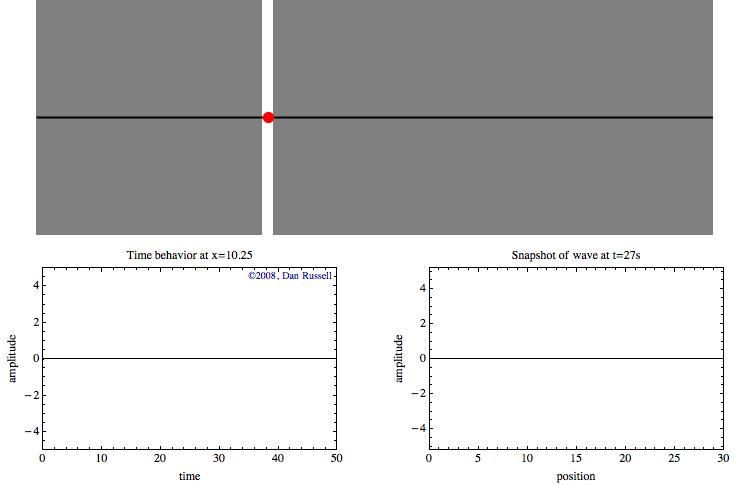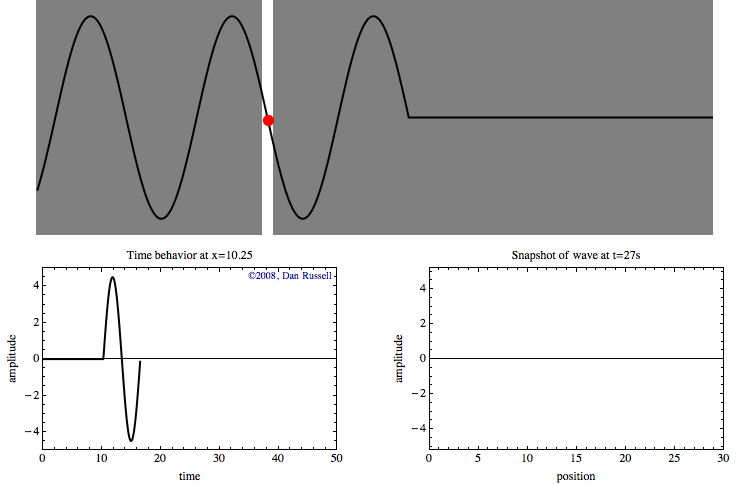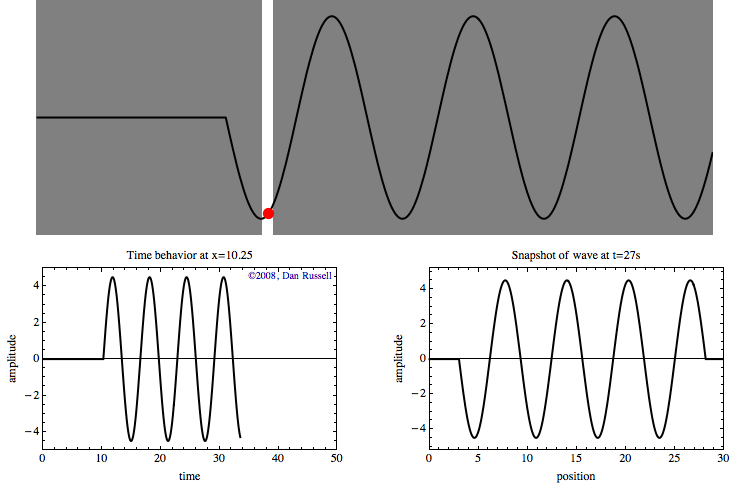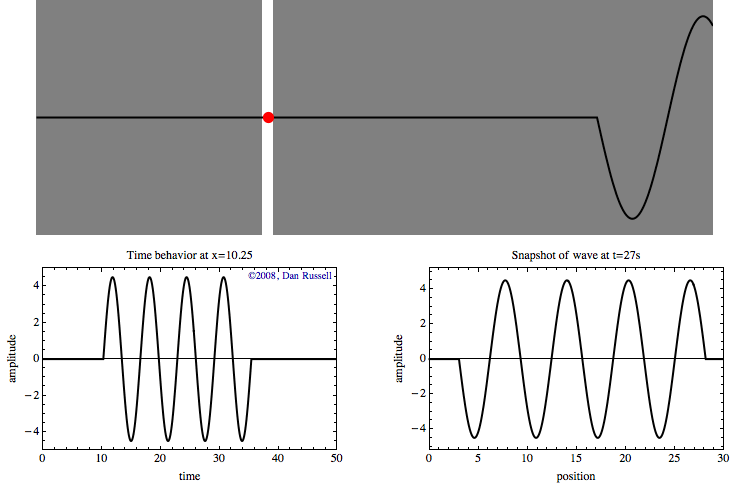
animation showing a wave train traveling from left to right along with a plot of the displacement of a point in the medium as a function of time, and a plot of the entire wave at a specfic time

The graph at lower left shows the time history of the motion of this red dot as the wave passes by. This graph represents the wave as a function of time for a specific location. Nothing happens for the first few seconds until the leading edge of the wave reaches the location of the red dot. Once the wave reaches that location, the red dot oscillates up and down with time as the wave passes through. After the wave pulse has passed through, the displacement returns to zero.

The graph at lower right represents a snap shot (a "photograph") of the wave at \(t=27\) seconds. The graph is blank for the first 26 seconds, then the graph appears all at once, and does not change. This graph represents the wave as a function of position at a specific time.