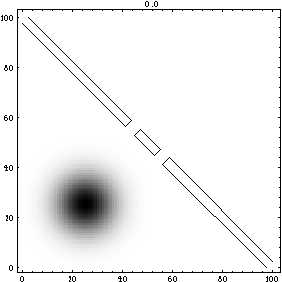
 A particle (wave function) passes through a double slit showing wave-like interference patterns.
A particle (wave function) passes through a double slit showing wave-like interference patterns.[ An efficient method for solving parabolic partial differential equations is implemented in Mathematica using InterCall and an external C routine. As an application, the two-dimensional time-dependent Schroedinger's equation is solved for various initial conditions and potential functions.]
Four different numerical experiments are given: a double slit experiment; tunneling (barrier penetration); scattering of a particle from a cylindrical potential barrier; and interaction of two wave-packets
 A particle (wave function) passes through a double slit showing wave-like interference patterns.
A particle (wave function) passes through a double slit showing wave-like interference patterns.
(This is the first frame of a 96992 byte mpg movie. Click on the graph to download the movie)
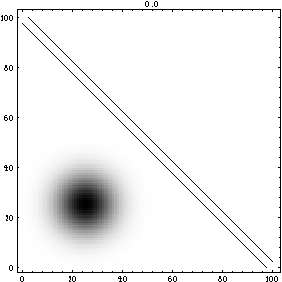 A particle (wave function) tunnels through, or penetrates, a rigid barrier. If you look closely you can see the faint evidence of the particle on the far side of the barrier. This phenomena is identical to frustrated total internal reflection of light waves at a boundary.
A particle (wave function) tunnels through, or penetrates, a rigid barrier. If you look closely you can see the faint evidence of the particle on the far side of the barrier. This phenomena is identical to frustrated total internal reflection of light waves at a boundary.
(This is the first frame of a 95045 byte mpg movie. Click on the graph to download the movie)
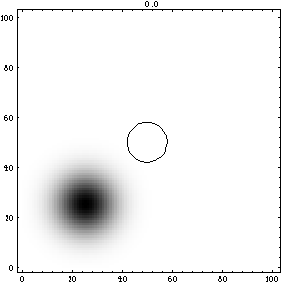 A particle (wave function) scatters from a rigid cylinder and shows interference phenomena.
A particle (wave function) scatters from a rigid cylinder and shows interference phenomena.
(This is the first frame of a 62319 byte mpg movie. Click on the graph to download the movie)
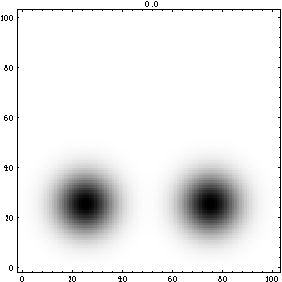 Two particles (wave functions) collide with each other, showing wave-like interference during the collision.
Two particles (wave functions) collide with each other, showing wave-like interference during the collision.
(This is the first frame of a 65999 byte mpg movie. Click on the graph to download the movie)