Acoustics and Vibration Animations

Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons License
This work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://www.acs.psu.edu/drussell/demos.html.

The content of this page was completely rewritten on October 18, 2018.

Vibrational Modeshapes of a Rectangular Membrane (fixed at the edges)

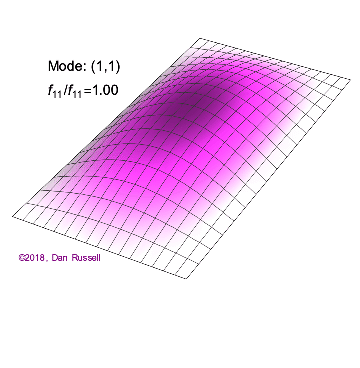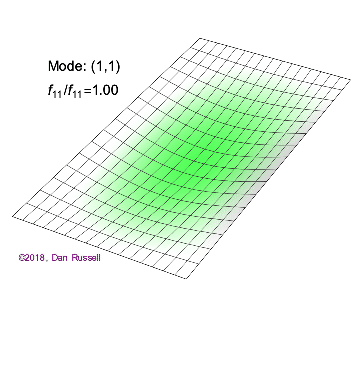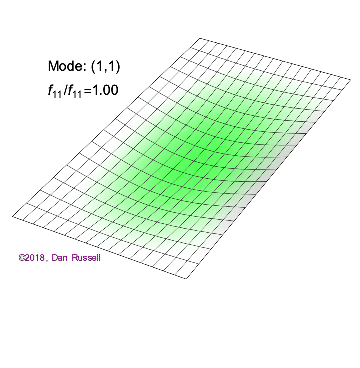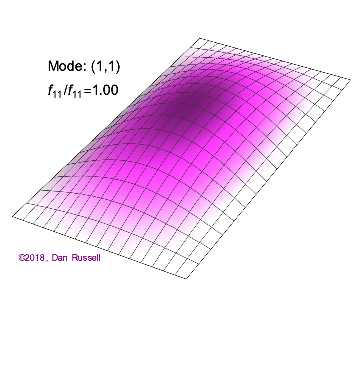
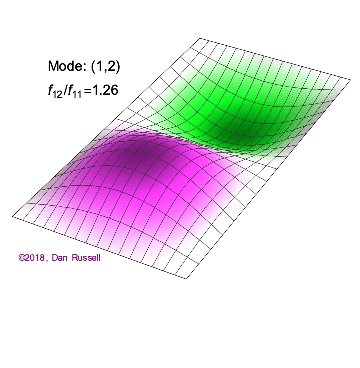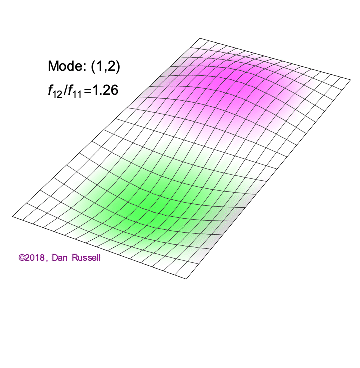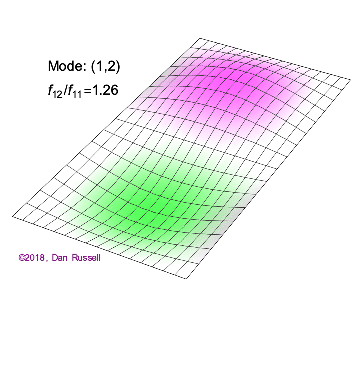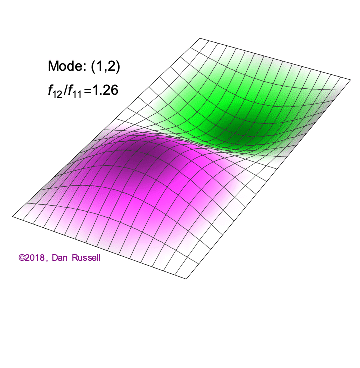
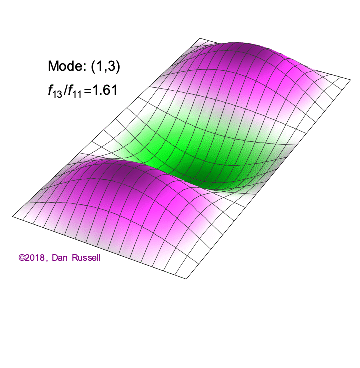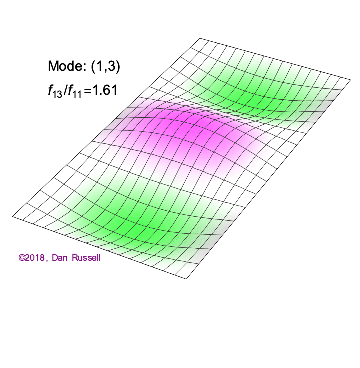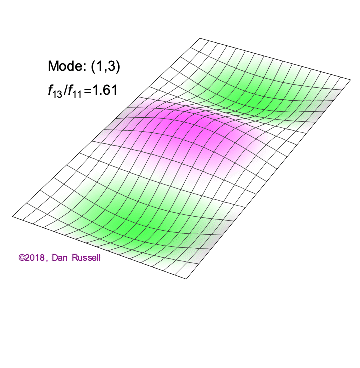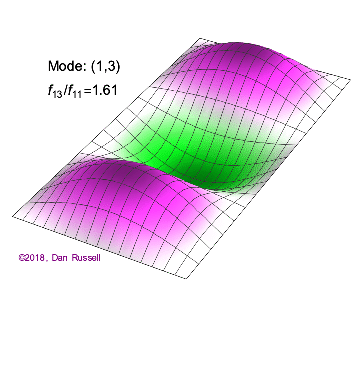
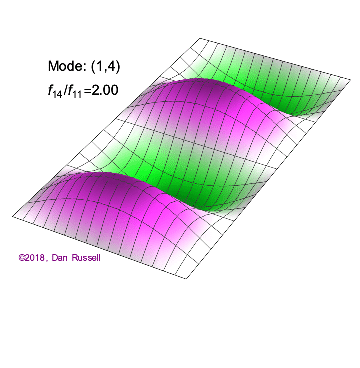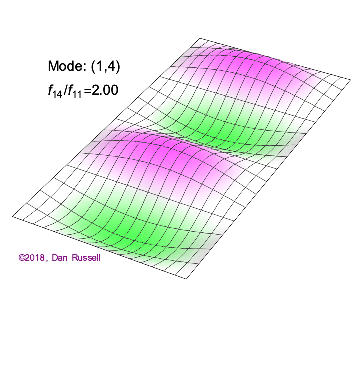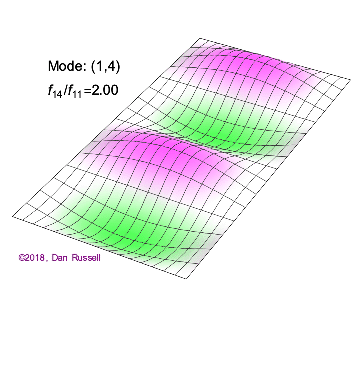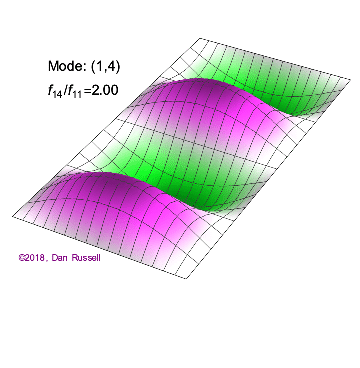
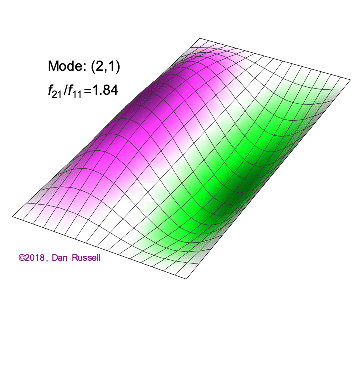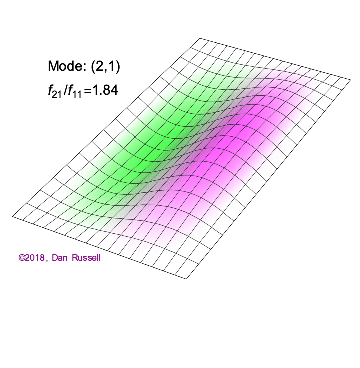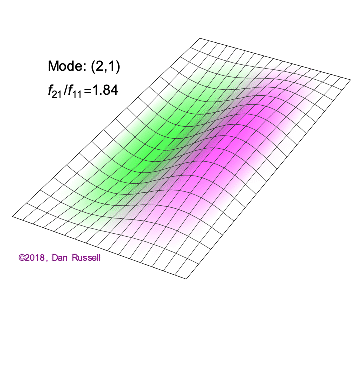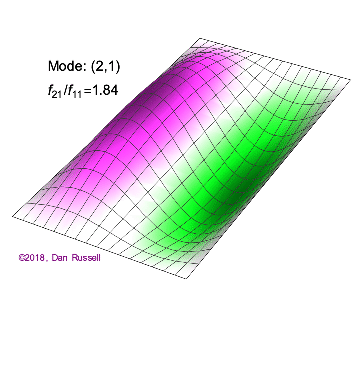
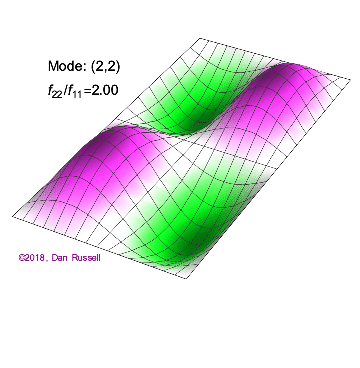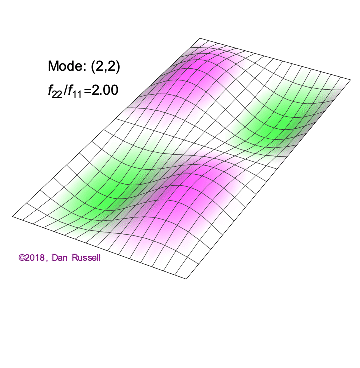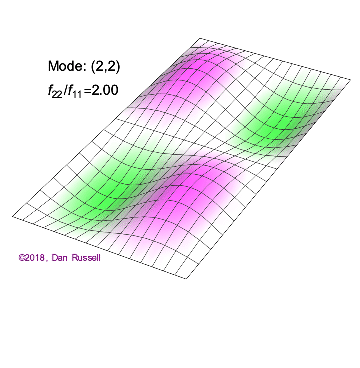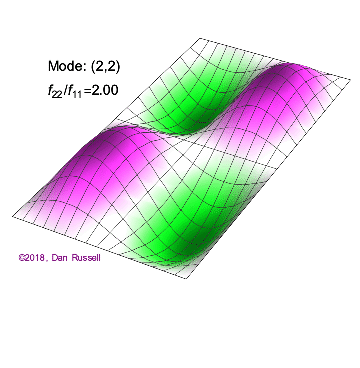
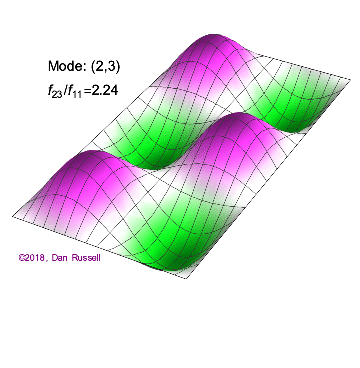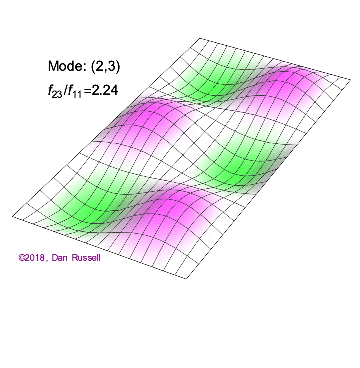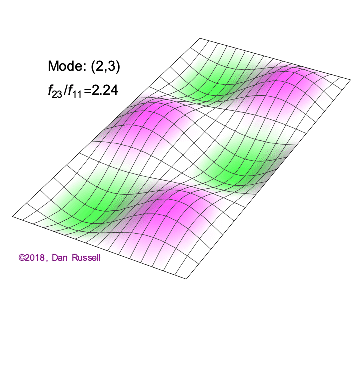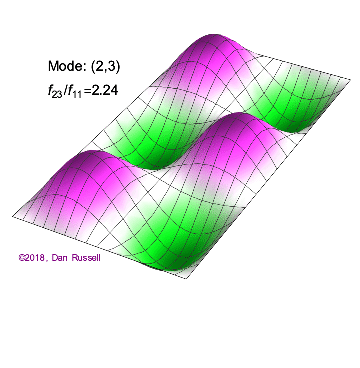
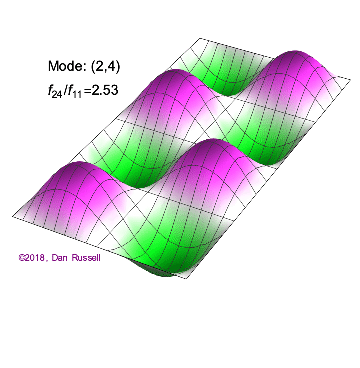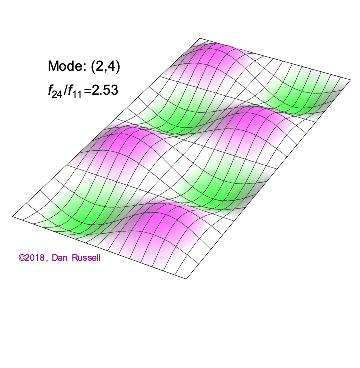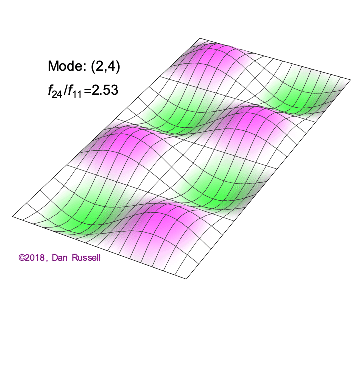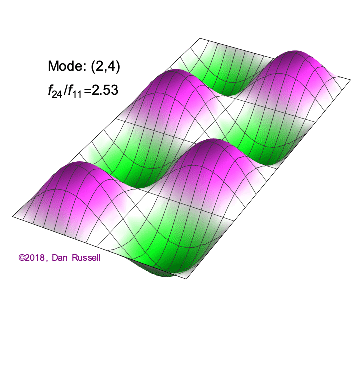
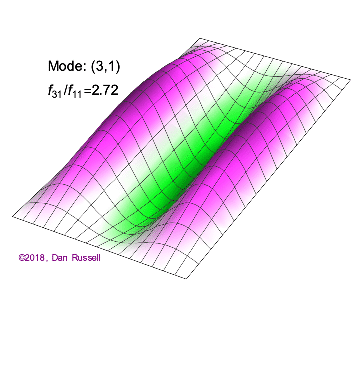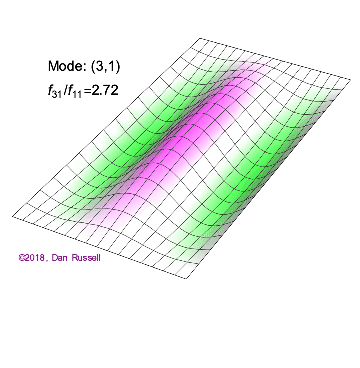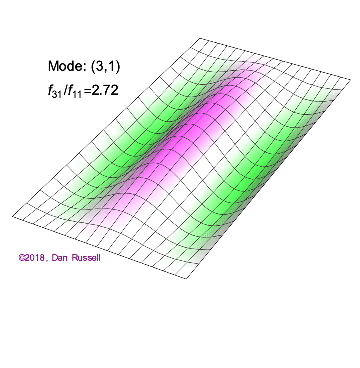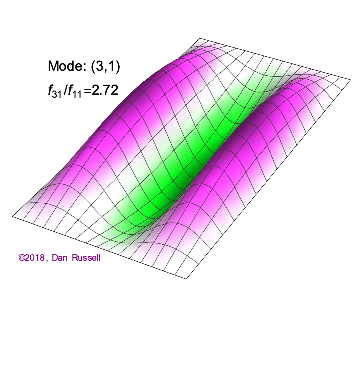
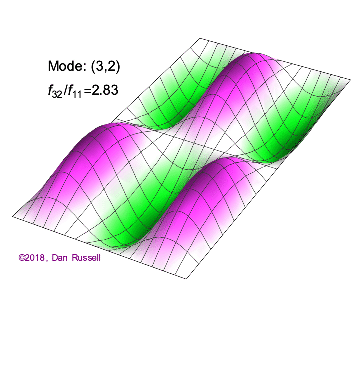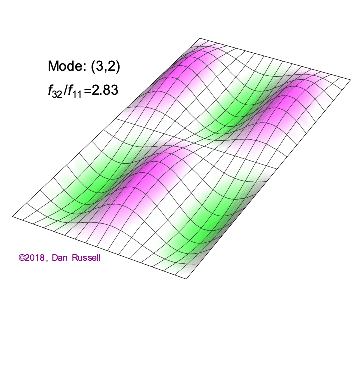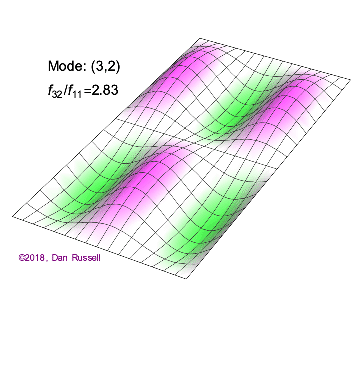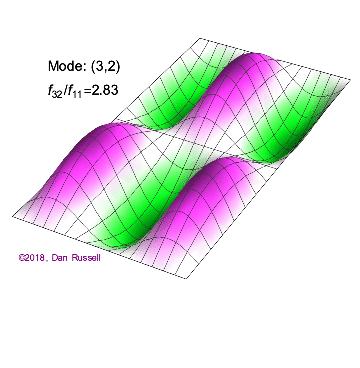
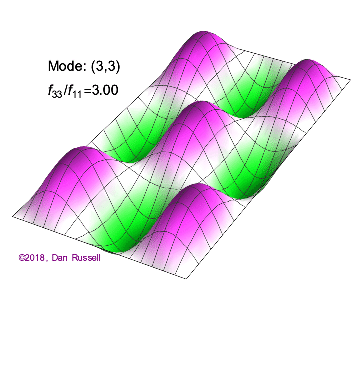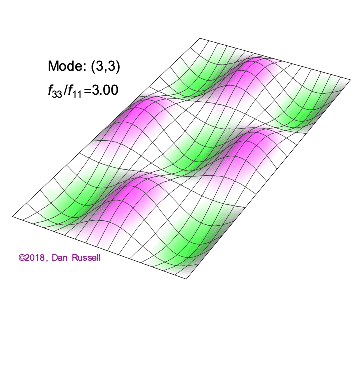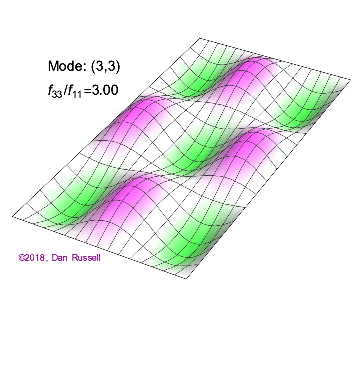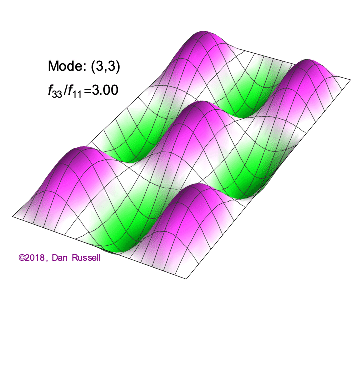
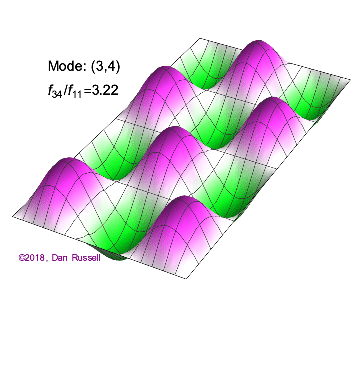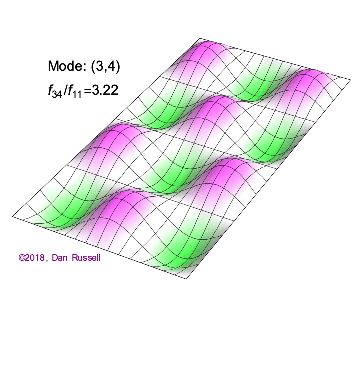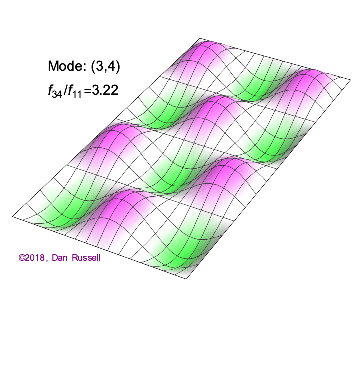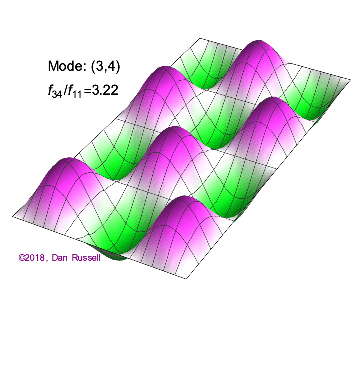
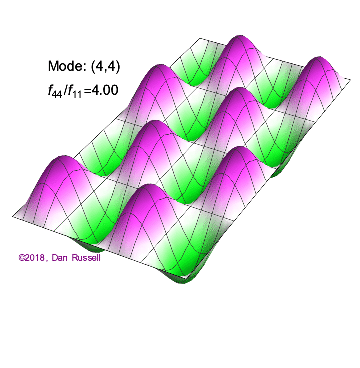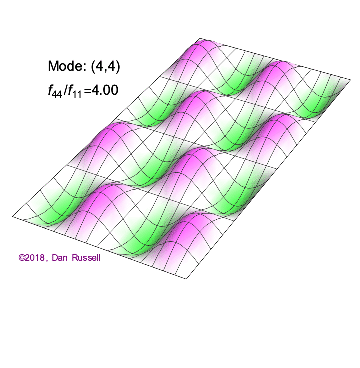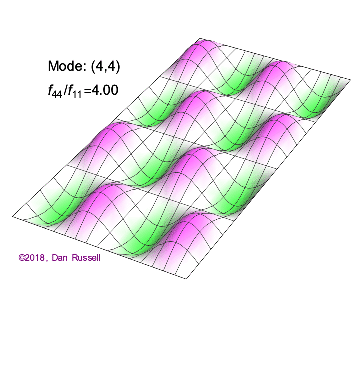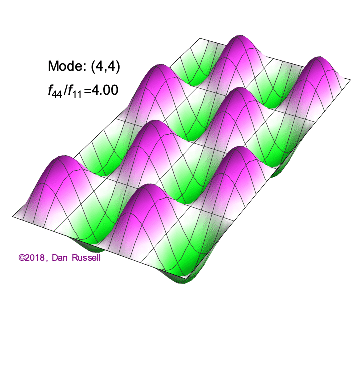
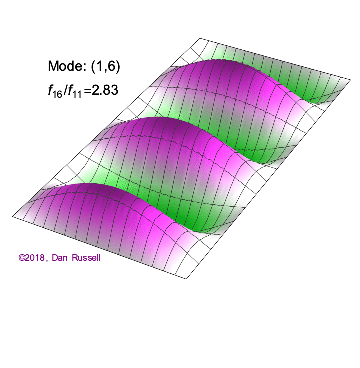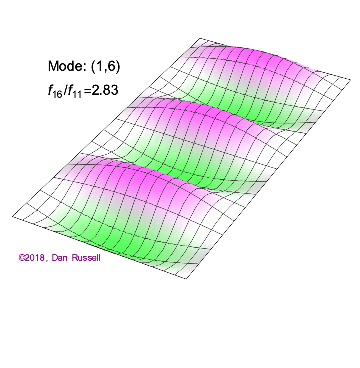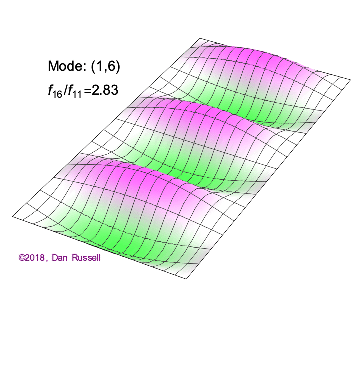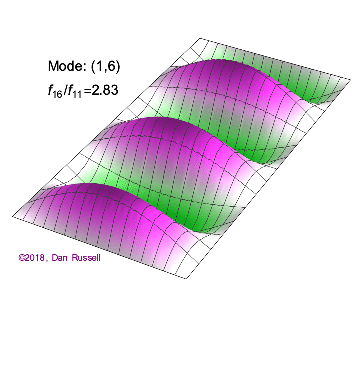
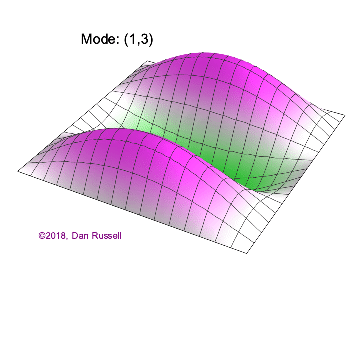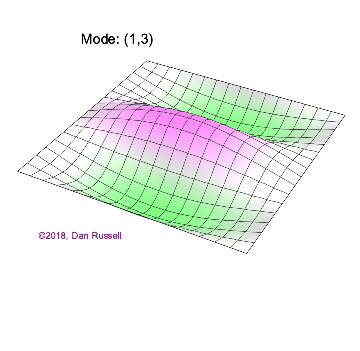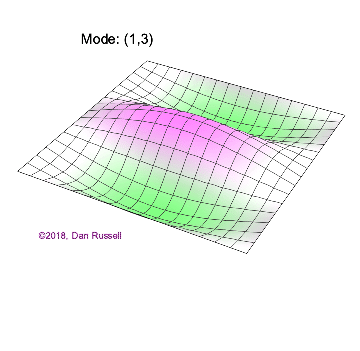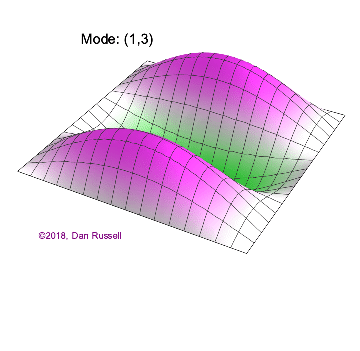
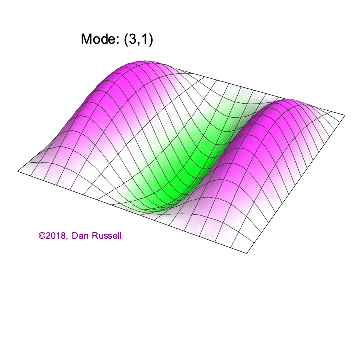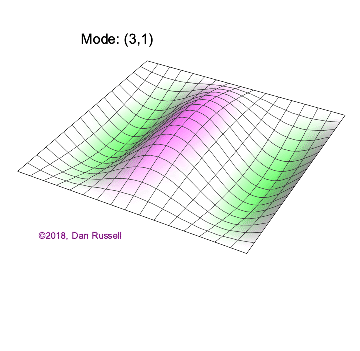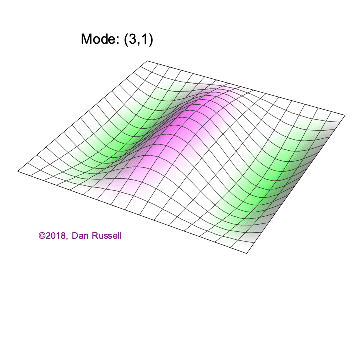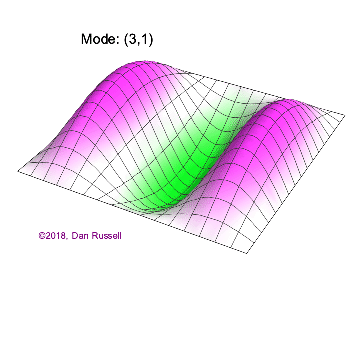
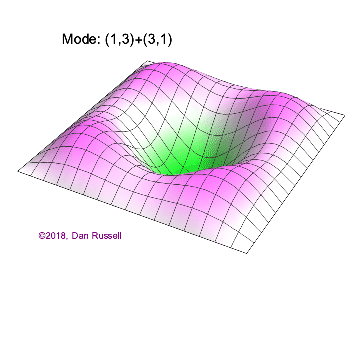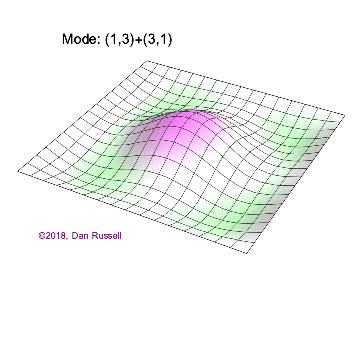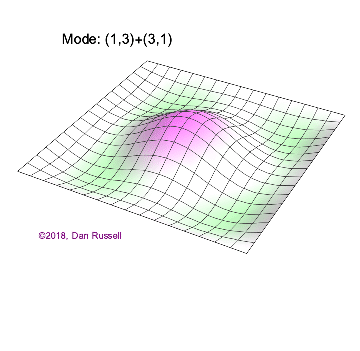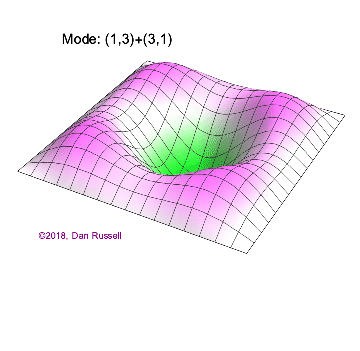
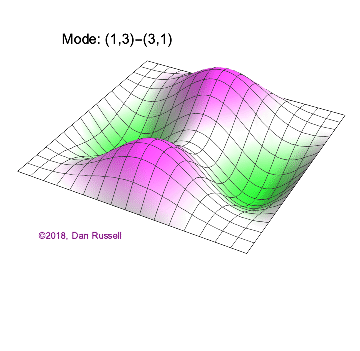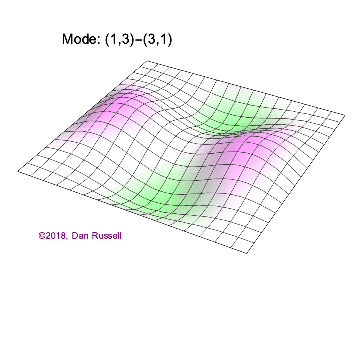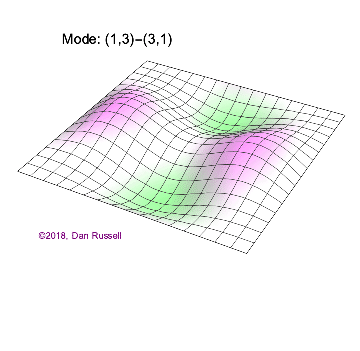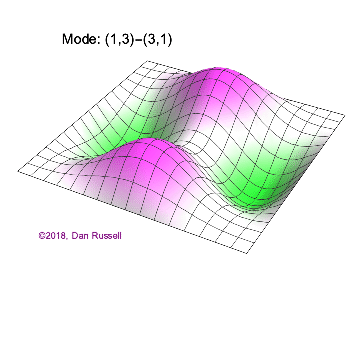
The mode shapes (standing wave vibrational patterns) for a rectangular membrane of width $L_x$ and length $L_z$, and which is fixed along all four edges, are given by $$ \Psi_{mn}(x,z) = \sin\bigg({m \pi \over L_x}x\bigg)\sin\bigg({n \pi \over L_z}z\bigg) \ .$$ The mode shape identifier (m,n) refers to the number of humps (antinodes) in the x and z directions, respectively. The number of nodal lines in a given direction is one less than the corresponding mode number. The natural (resonance) frequency for the (m,n) mode is $$ f_{mn}= {c \over 2}\sqrt{\bigg({m \over L_x}\bigg)^2 + \bigg({n \over L_z}\bigg)^2} \ . $$ Notice that the frequencies are strongly dependent on the dimensions (width and length) of the membrane. The same mode shape (m,n) could have a very different frequency if the dimensions of the membrane change.

Mode shapes for a Rectangular Membrane with $L_z = 2\,L_x$

Integer Frequency Ratios

A 2-D membrane is often described as simply being a 2-D version of an elastic spring, and while the similarities are some similarities, there are also several important ways that membranes are different from strings. For a string, the frequencies $f = {n c \over 2 L}$ are all integer multiples of the fundamental (n=1) mode.

However, as the above mode shapes illustrate, the situation is a little different for a rectangular membrane. Regardless of the dimensions, there are a set of modes which will always be integer multiples of the fundamental for a rectangular membrane $\longrightarrow$ $f_{22} = 2\, f_{11}$,  $f_{33} = 3\, f_{11}$,   $f_{44} = 4\, f_{11}$,   $f_{55} = 5\, f_{11}$ and so on.

Depending on the ratio of dimensions, $L_z/L_x$, there might be other mode shapes which are also integer multiples of the fundamental, like the $f_{14} = 2\, f_{11}$ in the above example where $L_z = 2\,Lx$. However, the majority of other mode shapes will not be integer multiples of the frequency for the (1,1) mode. Furthermore, there is no consistent ordering of mode shapes according to frequency. The frequency order in which modes appear is entirely dependent on the ratio of dimensions, $L_z/L_x$.

Degenerate Modes

A second way that a rectangular membrane is different from a string, is that it is possible for two different mode shapes to have exactly the same frequency. For the membrane modes shown above, for which $L_z = 2\,L_x$, the (2,2) and (1,4) modes both have the same frequency of $2.00\,f_{11}$. Similarly, the (3,2) and (1,6) modes both have the same frequency $2.83\,f_{11}$.

These are called Degenerate Modes, and if the membrane is excited at this frequency, all of the degenerate modes will oscillate at the same time and the result will be a superposition of all of the degenerate mode shapes.

As a specific example, consider a square membrane with $L_x = L_z = L$. For a square membrane, the frequency for the (m,n) mode is $$ f_{mn}={c \over 2L}\sqrt{m^2 + n^2} $$ with the result that $f_{mn} = f_{nm}$. The general response of the membrane vibration will be the superposition of the two degenerate modes $$ \Psi = a\,\Psi_{mn} + b\,\Psi_{nm} \qquad \hbox{with}\qquad a^2 + b^2 = 1 \ .$$ The animations below show four possible configurations for a square membrane, all of which exist at the same frequency.

Why The Choice of Pink-Green Color Scheme?

Something I have become consciously aware of recently is the importance of using color schemes that can be seen by the significant population of people who have some sort of color blindness. The traditional rainbow (or "jet") color schemes are extremely poor for a number of reasons, including the fact that they don't work well for color-blindness. And, a red-white-blue color scheme that I had been using also does not work well for several kinds of color-blindness. A recent development in computational modeling software like COMSOL is the adoption of a new cividis color scheme that looks almost exactly the same to people with and without most common forms of color blindness. The cividis color scheme is not (yet) available in Mathematica and I have not had the time to create my own color scheme that mimics cividis (whatever "spare" time I do have is spent on creating new animations). But, the pink-green color scheme is one that - while it doesn't look exactly the same to people with normal eyesight and with various forms of colorblindness - does result in two contrasting colors for everyone except those who cannot see colors at all. The image below was created with the help of a Color Blindness Simulator and shows that for almost all cases, a contrasting color pattern may be detected that clearly distinguishes between the regions with opposite phase.