Crankshaft Motion
An Example of a Non-Harmonic Oscillator
The animations on this page were inspired by an example described in the following paper:
- Eli Maor, "A Repetoire of S.H.M.," The Physics Teacher, 10(7): 377-382 (1972). https://doi.org/10.1119/1.2352279
The crankshaft: a sinusoidally driven, non-harmonic oscillator
Quite often, when learning about oscillation, students assume (or are led to believe) that all oscillating systems exhibit harmonic oscillation. It is assumed that a system which undergoes periodic motion may be described using a cosine function: \[ x(t) = A \cos(\omega t + \phi) \,. \]
However, there are plentiful examples of systems that undergo periodic motion, but whose motion is not described by a sinusoidal function. One such system is a crankshaft - a piston whose linear reciprocating motion is driven by a wheel which is rotating with a constant angular velocity. As indicated in the figure at right, as the blue wheel rotates counterclockwise with a constant angular velocity, the crankshaft (fixed length L) makes the piston point (red dot) oscillate back and forth in along the x-axis.
The relationship beween length of shaft, radius of rotator, and position x of the end of the shaft. \[ L^2 = a^2 + x^2 - 2\, a\, x\, \cos\omega t \] So, the positon of the end of the end of the shaft is given by: \[ x(t) = a \cos\omega t - \sqrt{L^2 - a^2\sin^2\omega t} \]
Long crankshaft approximates simple harmonic motion
In the limit of a long shaft, so that \( L>>a \), the displacement function approximates to \( x(t) \approx a \cos(\omega t) - L \) which is sinusoidal. This is illustrated in the animation below, for the case where the shaft length is seven times the wheel radius (\(L=7a\)). As the wheel rotates counterclockwise, the far end of the crankshaft oscillates sinusoidally along the x-axis. The graph on the right shows the horizontal motion of the shaft end (red dot) as a function of time; the plot looks sinusoidal.
Short crankshaft exhibits periodic, but non-harmonic motion
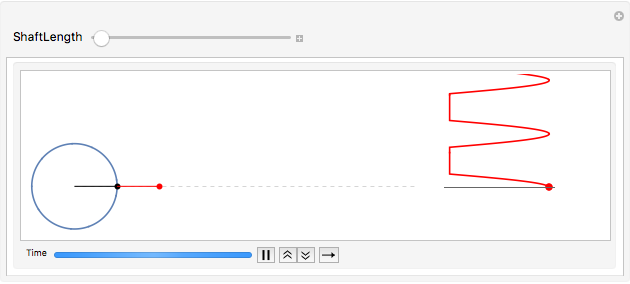
As the crankshaft length shortens, the simple approximation is no longer valid. The motion remains periodic (with the same period) but is no longer sinusoidal. The animation below shows the result when the crankshaft length is twice the radius of the wheel (\(L=2a\)).
The non-sinusoidal nature of the oscillation becomes more apparent as the crankshaft length shortens even more. Here, the shaft length is \(L=1.2a\).
If \(L=a\), the equation for position becomes\(x(t)=0\) and the piston gets stuck at the center and does not oscillate. Since the value of \(\sin^2\omega t \le 1\), there is not a real solution if \(L < a\).
Click on the image at right to download the interactive Mathematica notebook used to create these animations.