Acoustics and Vibration Animations
Daniel A. Russell
Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons License CC BY NC ND This work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License . Based on a work at http://www.acs.psu.edu/drussell/demos.html . Additional information about using this content is available at http://www.acs.psu.edu/drussell/Demos/copyright.html .


The animations on this page were originally created by Victor W. Sparrow between 1992-1998. They were assembled and presented on this page on May 17, 2018.
HTML code was updated for WCAG accessibility and HTML5 compliance on August 19, 2025 .

Vic Sparrow's Acoustics and Vibration Animations

Giving Credit where Credit is Due

My own Acoustics and Vibration Animations. website has received a rather significant amount of attention in the acoustics education community since I first started posting animations back in 1997. I would like to publicly acknowledge that I learned how to make animations visualizing acoustics and vibration phenomena many years ago from Dr. Vic Sparrow. The animations he showed in the classes I took from him inspired me to learn to make my own.


Dr. Victor W. Sparrow is currently the United Technologies Corporation Professor of Acoustics in the Graduate Program in Acoustics. He is an internationally recognized expert on sonic booms generated by aircraft and the propagation of those sonic booms through the atmosphere. Dr. Sparrow teaches a number of important core and elective graduate courses in acoustics:

  • ACS 501 -- Elements of Acoustics and Vibration
  • ACS 502 -- Elements of Waves in Fluids
  • ACS 515 -- Acoustics in Fluid Media
  • ACS 540 -- Nonlinear Acoustics
  • ACS 544 -- Computational Acoustics
  • ACS 533 -- Outdoor Propagation of Sound
  • ACS 551 -- Spatial Hearing and 3D Audio
Way back in 1991 when I began studying toward the Ph.D. in Acoustics from the Graduate Program in Acoustics at Penn State, Dr. Sparrow was a newly hired Assistant Professor of Acoustics. I was the second graduate student he took on. He was working on a number of projects at the time -- his first two Ph.D. students wrote theses on gas lattice vibrations and fuzzy structures (mine). But, one of his areas of interest back then was the visualization of scientific phenomena. Dr. Sparrow used Mathematica to create a number of animations to visualize various wave and vibration phenomena, and he used these animations when he taught ACS 501, 502, and 515 (I took 502, 515, Computational Acoustics and Nonlinear Acoustics from him).


Inspired by his animations, I started to learn how to make my own animations with Mathematica. I recently gained access to some old computer archives, and found a repository of old animations that Dr. Sparrow had created back in the 1990's when I was his student. I converted these old Quicktime MOV files into animated GIF files and have posted them here so that others can enjoy the elegance and the craftsmanship that inspired me to begin making my own animations.


These animations are shared here (for historical and nostalgic reasons), with Vic's permission. They are presented without much commentary -- as I have created similar animations with detailed explanations for most of these concepts on my website.

Vic Sparrow's Animations for Vibration (ca 1992-1998)

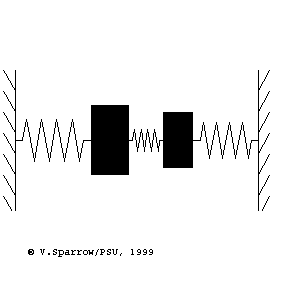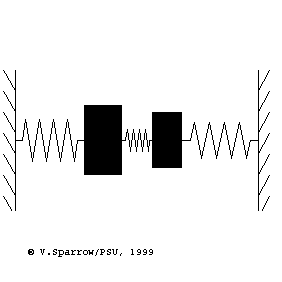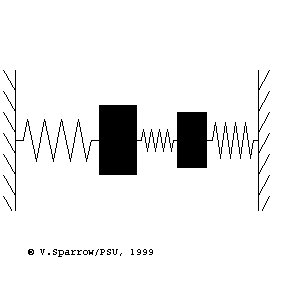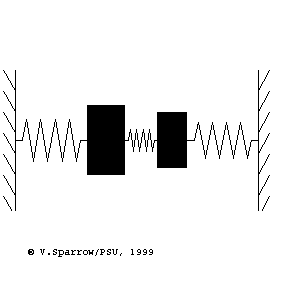
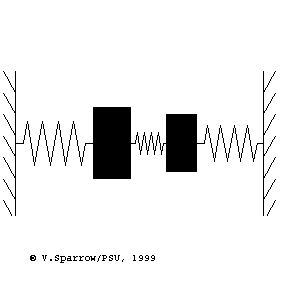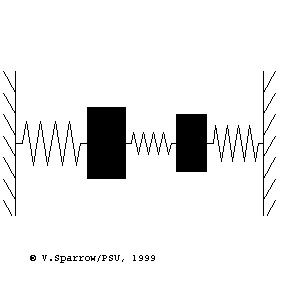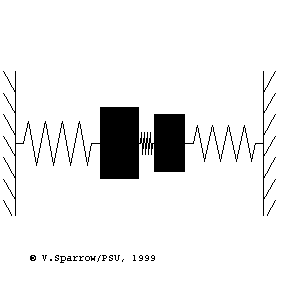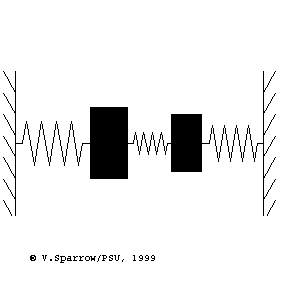
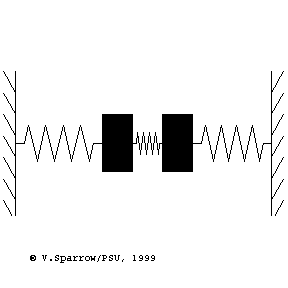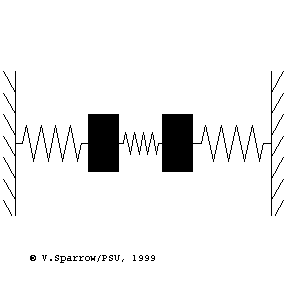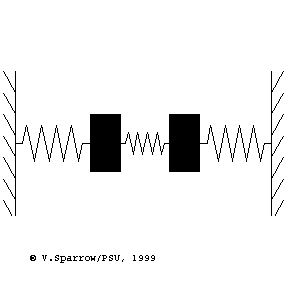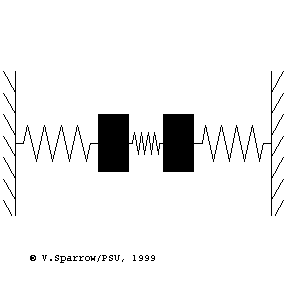
Modes of a 2-dof mass-spring system

From left to right: (Left) lowest frequency mode where both masses move in-phase in the same direction at the same time. (Middle) higher frequency mode where the masses move with opposite phase, in opposite directions. (Right) coupled motion where energy swaps back and forth between the two masses.
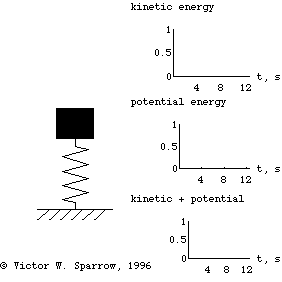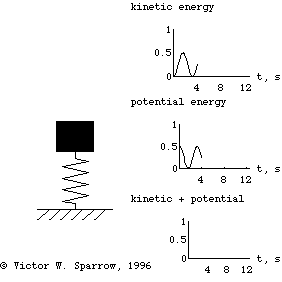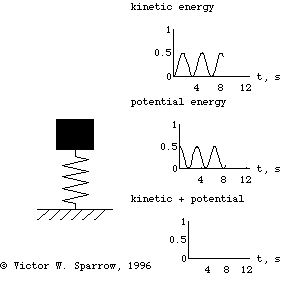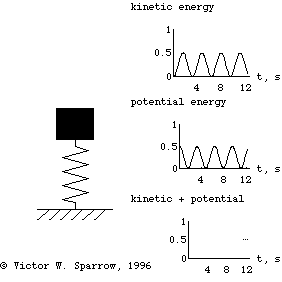
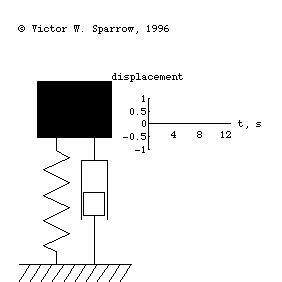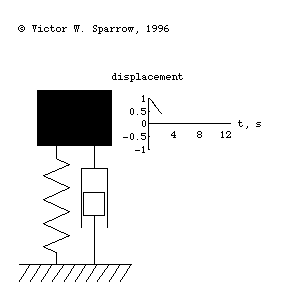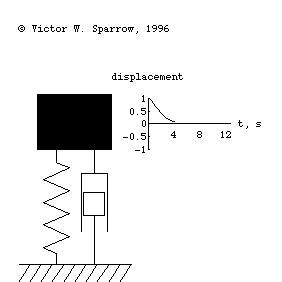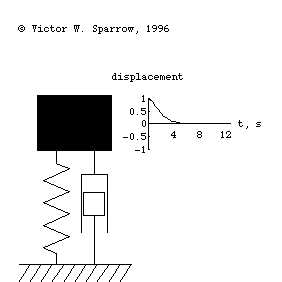
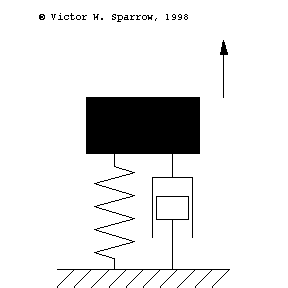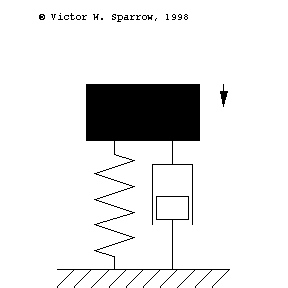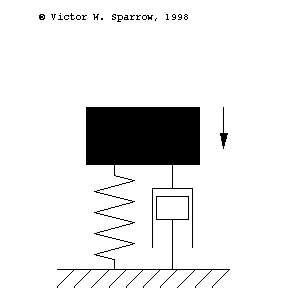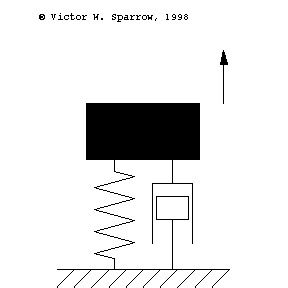
animation animation animation


Oscillation of a 1-DOF Mass-Spring System, Damping, and Forced Response

(Left) A mass-spring simple harmonic oscillator. (Right) Exchange of Kinetic and Potential Energies as the mass-spring system oscillates
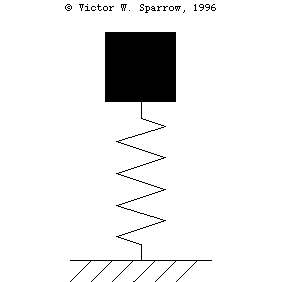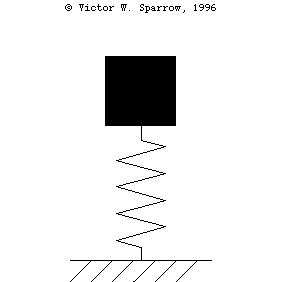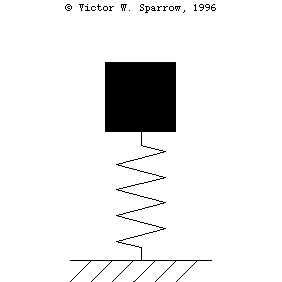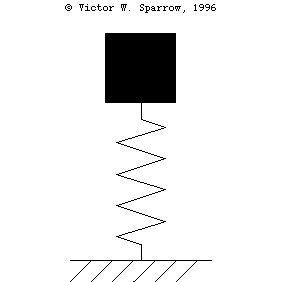
animation animation

From Left to Right: [1] Under-damped mass-spring system. [2] Critically-damped mass-spring system. [3] Over-damped mass-spring system.
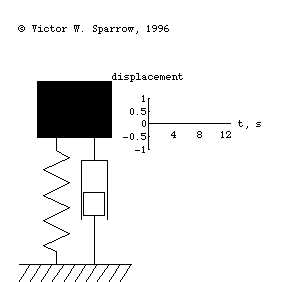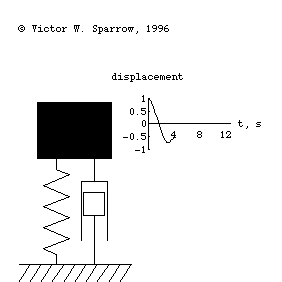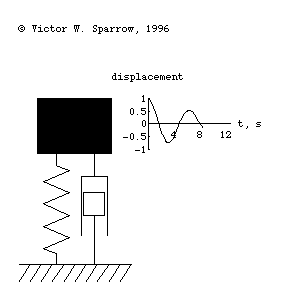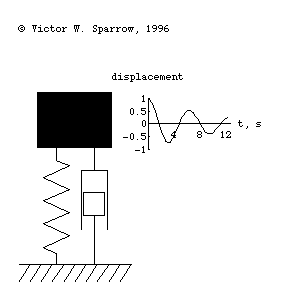
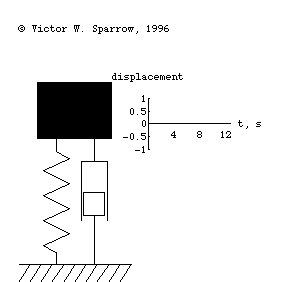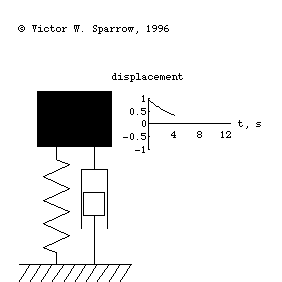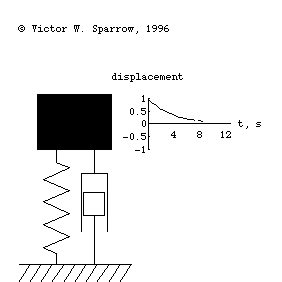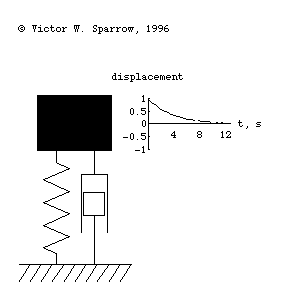
animation animation animation

Forced, damped mass-spring system being driven at resonance.
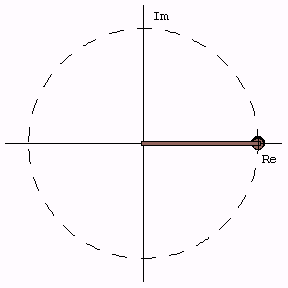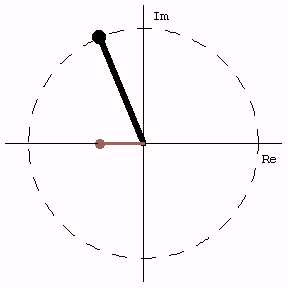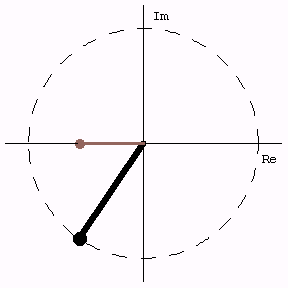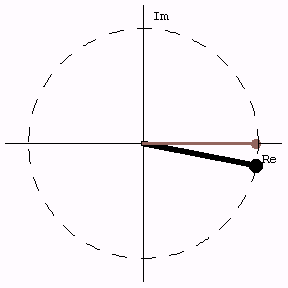
animation


The Unit Circle

Comparing rotation (phasor) around the unit circle with the real part, which represents oscillation back and forth along the horizontal axis.
animation


Flexural Bending Modes of a Free-Free Beam

The first three modes of vibration of a free-free beam, and a much higher frequency mode.
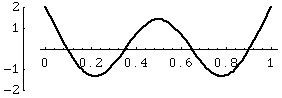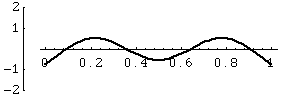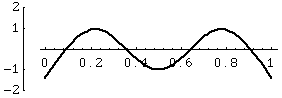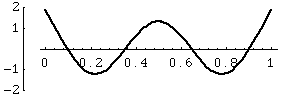
animation animation animation animation


Modes in a Square Membrane

The first three modes of vibration of a square membrane, fixed at the edges.
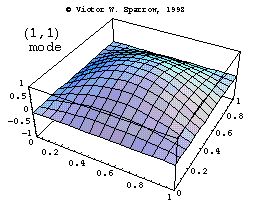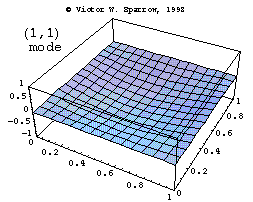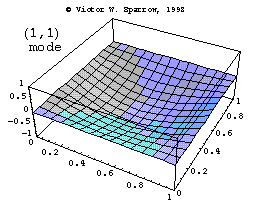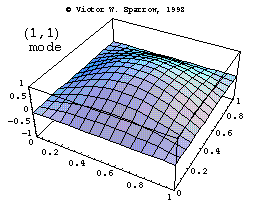
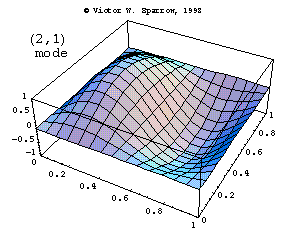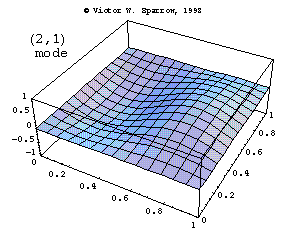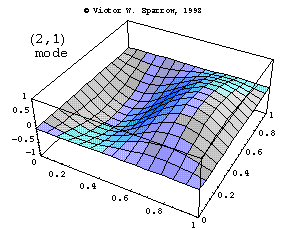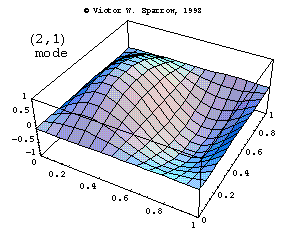
animation animation animation

Vic Sparrow's Animations for Sound Waves (ca 1992-2001)

Superposition of Two Wave Pulses

(Left) Leftward traveling rectangular pulse. (Middle) Rightward traveling sinusoidal pulse. (Right) Superposition of these two pulses.
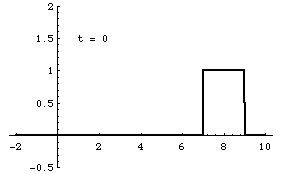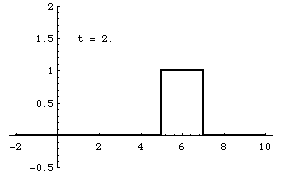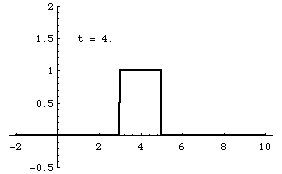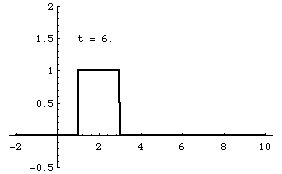
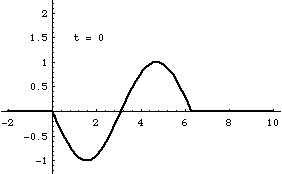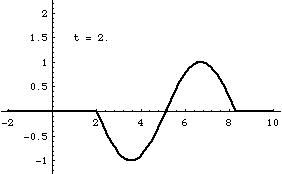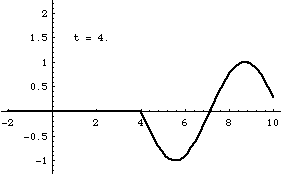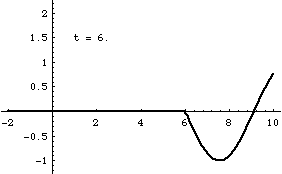
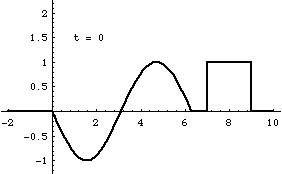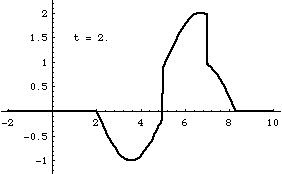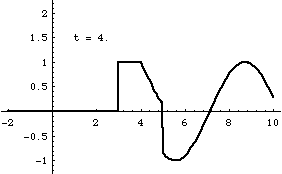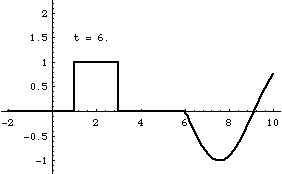
animation animation animation


Superposition and Standing Waves

From left-to-right: [1] Right-traveling sine wave. [2] Left-traveling sine wave. [3] Superposition of these the right and left going waves results in a standing wave. [4] If the amplitudes of the right- and left-going waves are not exactly the same, the superposition result is not quite a standing wave. In this case, the amplitude of the right-going wave is slightly larger than the left-going wave.

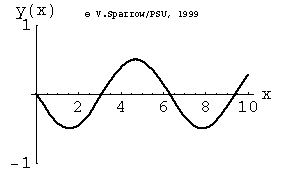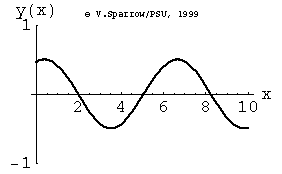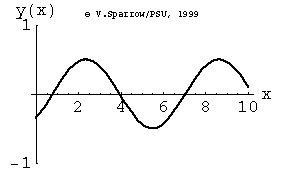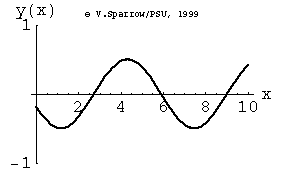
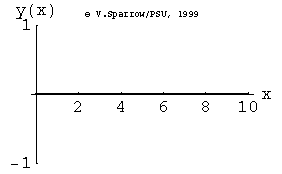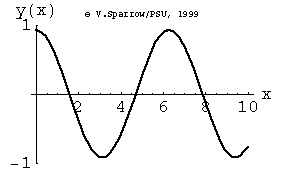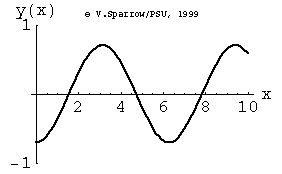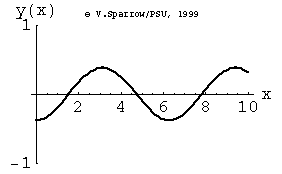
animation animation animation animation


Monopole, Dipole, and Quadrupole Sources

(Left) A radially oscillating (pulsating) sphere - a monopole source. (Right)> A transversely oscillating sphere - a dipole source.
animation animation


(Left) spherical sound wave created by a monopole source. (Right)> spherical sound wave created by a dipole source.

animation      animation


(Left) Two versions of a dipole-type source: two oppositely phased monopoles, and a transversely oscillating block. (Right)> Two versions of a lateral quadrupole-type source: each consisting of two oppositely phased dipoles.
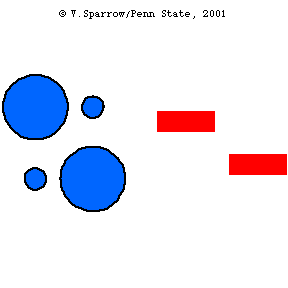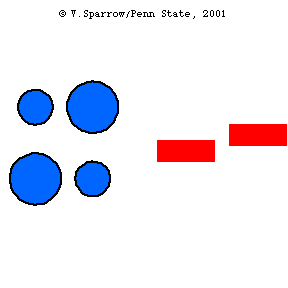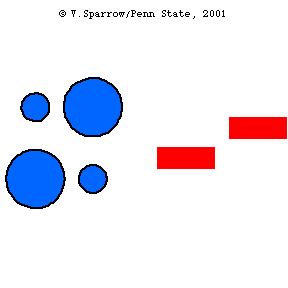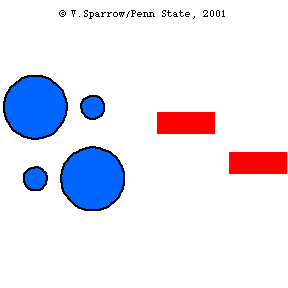
animation      animation


Plane Waves and Pistons

Piston driven, longitudinal plane waves in a tube.

animation


(Left) Piston oscillating in a rigid baffle. (Right) high frequency (ka=15) on-axis sound pressure radiated by a circular baffled piston

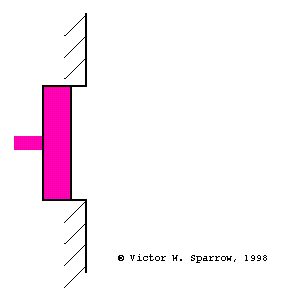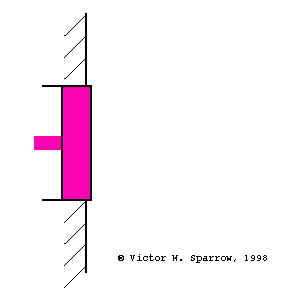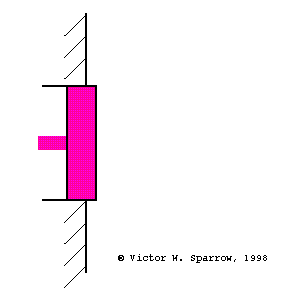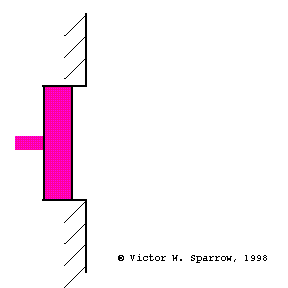
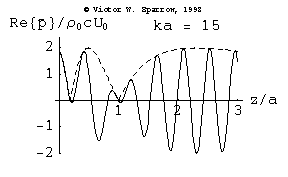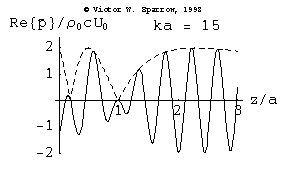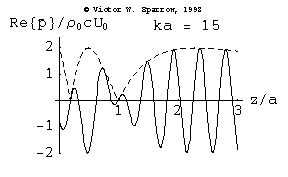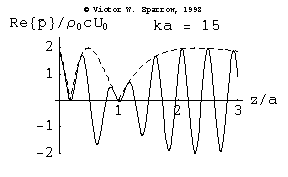
animation animation


Pressure, Velocity, and Absorbing Layers

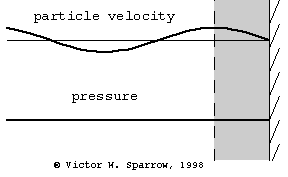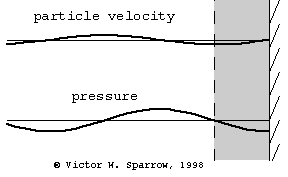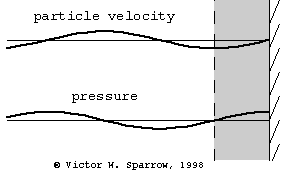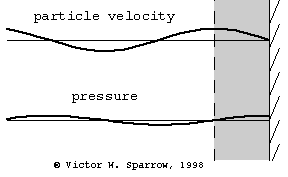
(Left) Particle velocity near a rigid wall is zero at the wall and maximum at a distance of 1/4 wavelength form the wall. A layer of absorbing material must be at least 1/4 wavelength thick in order to engage the sound wave at a location where the particle velocity is maximum (and thus produce maximum absorption through viscous losses) with a layer of absorbing material which is 1/4 wavelength thick. (Middle) Same as the left plot, but this time also showing the pressure (90o out of phase with velocity). (Right) Maximum absorption may also be achieved with a thin layer of absorbing material placed 1/4 wavelength from the wall.
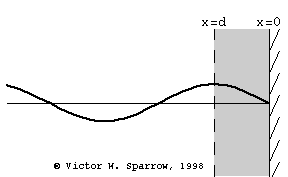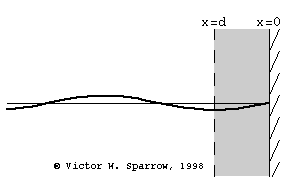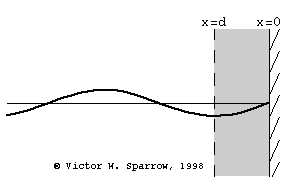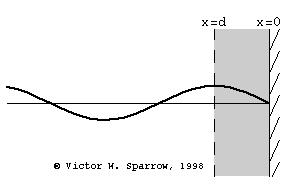
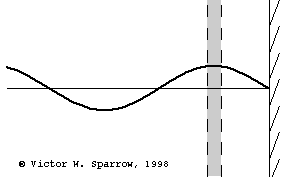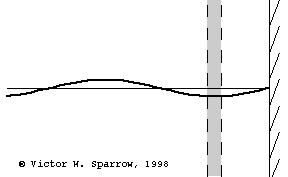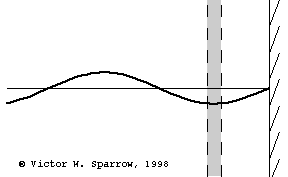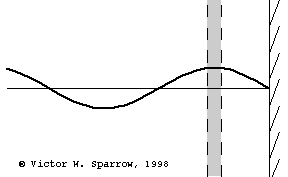
animation animation animation


Resonant Absorber Devices

(Left) Helmholtz Resonator Absorber (Right) Tuned Plate (Panel) Absorber

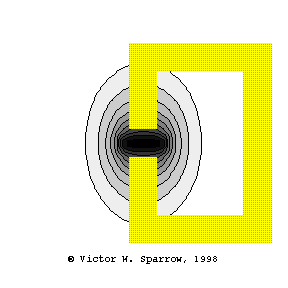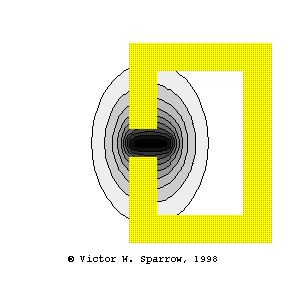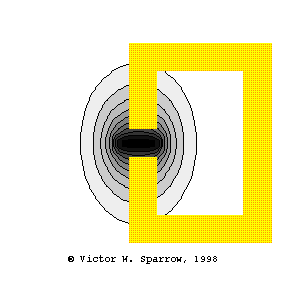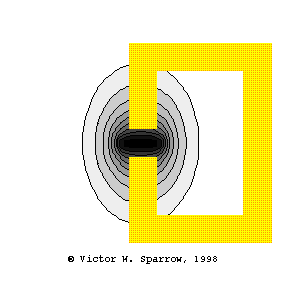
animation animation


Coincidence -- Matching Trace Velocity

A plane wave in air is incident upon a wall, such that the trace velocity of the plane wave matches the velocity of bending waves in the wall. This is called "coincidence".

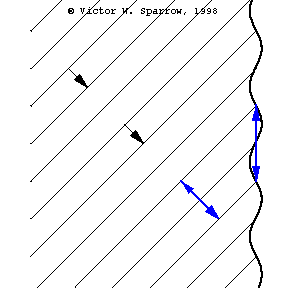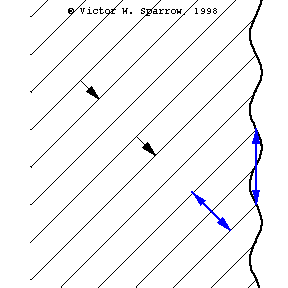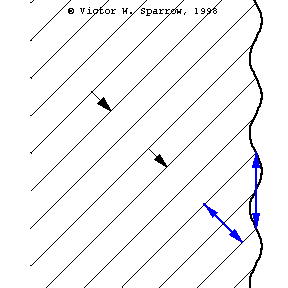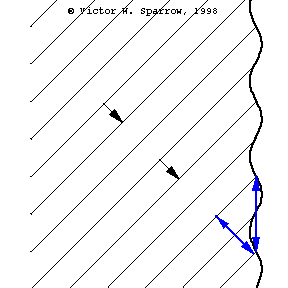
animation


Phase Speed and Group Speed

A wave packet travels to the right at the group speed. The dot indicates the phase speed (moving with the peak of a wave within the envelope). In this case, the phase speed is greater than the group speed.

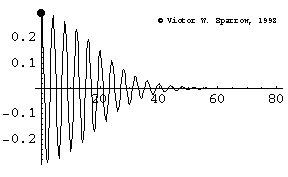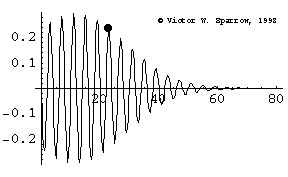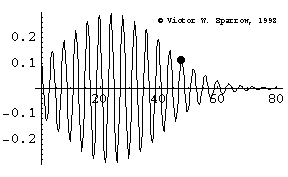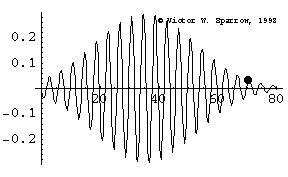
animation


Lattice Gas Model of a Lossy Wave

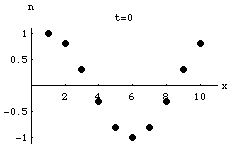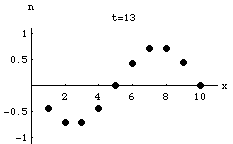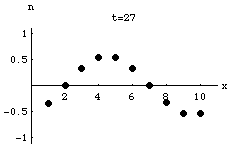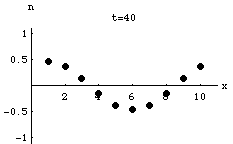
animation


Exponential Attenuation as a Wave Propagates

animation