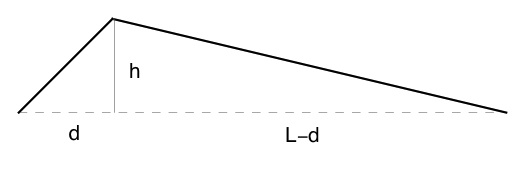
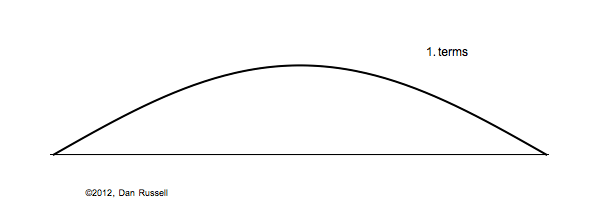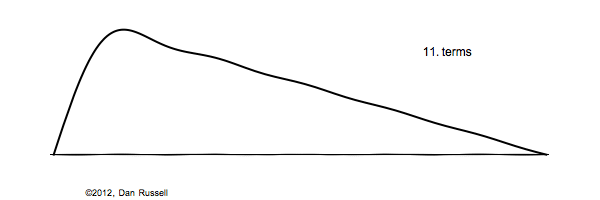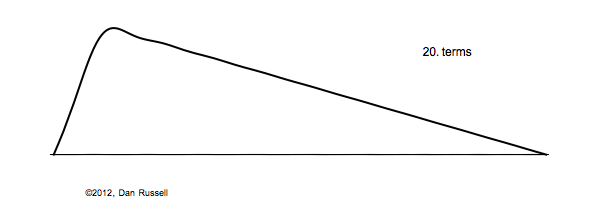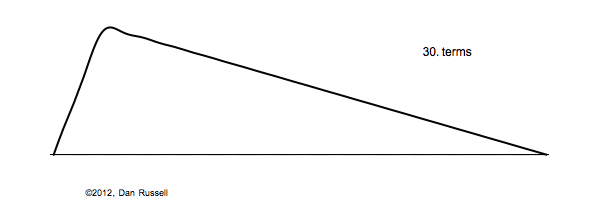
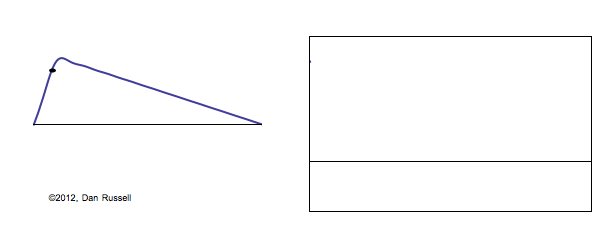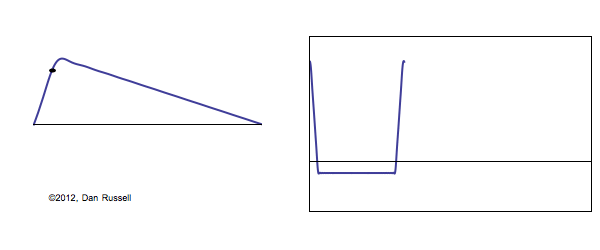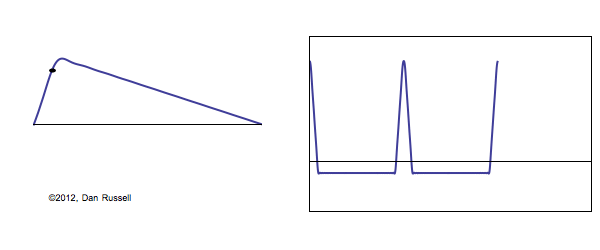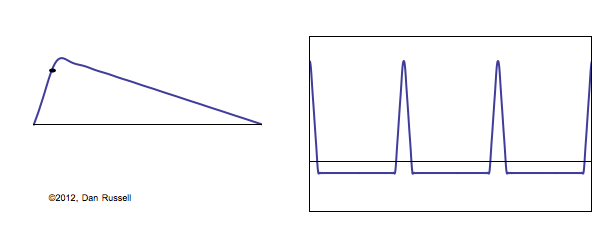
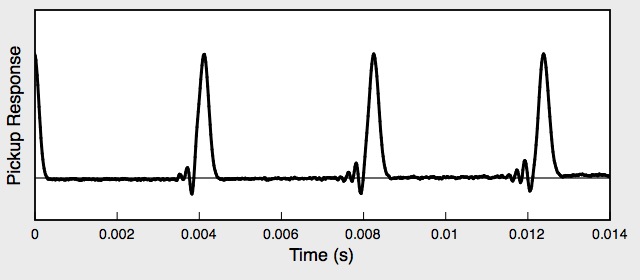
Most of the animations on this page were created in 2012, but the content of this page was originally posted on August 7, 2020.

The Plucked Fixed-Fixed String

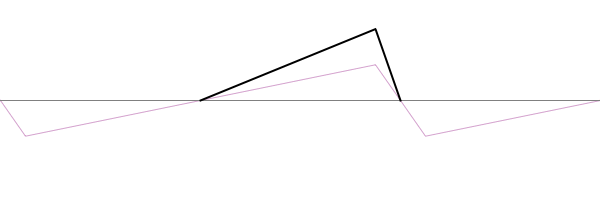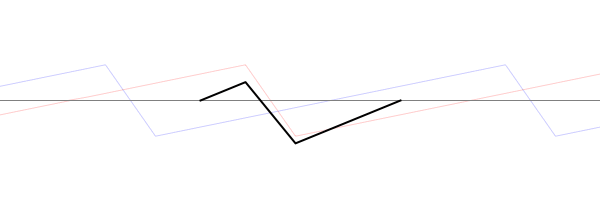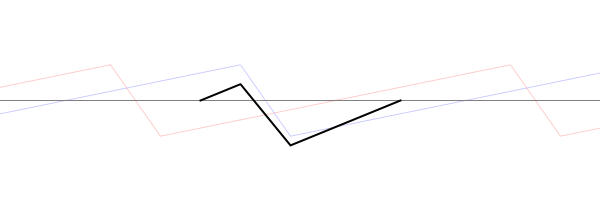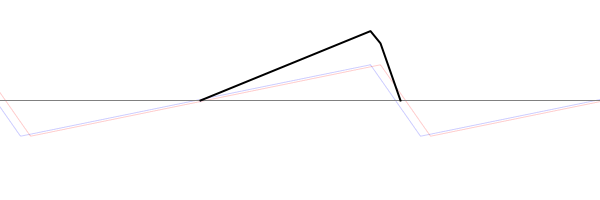
When solving the problem of a plucked string, fixed at both ends, there are two types of conditions which must be considered. The Boundary Conditions (ie, the values of displacement, velocity, and force at the each end of the string) determine the possible allowed mode shapes with which the string may vibrate at one of its natural frequencies. The Initial Conditions (the initial displacement and velocity of the entire string at time $t=0$) determine which of the possible allowed mode shapes actually participate in the ensuing motion, and with what amplitudes.

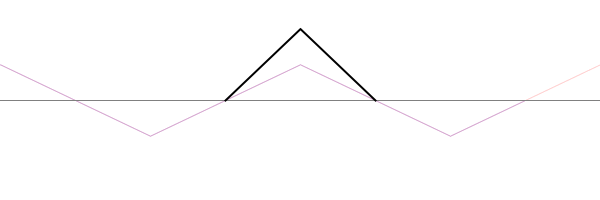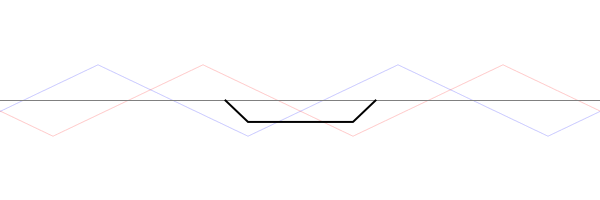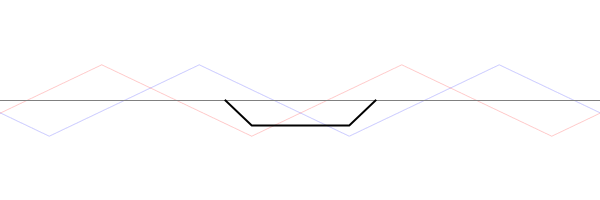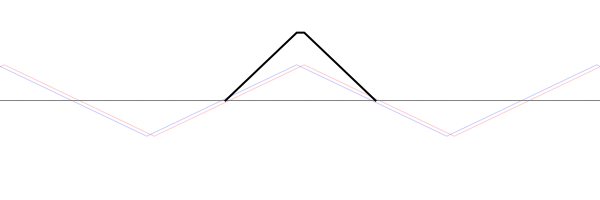
For a string which is fixed at both ends, the boundary conditions at each end require that the displacement of the string must always be zero. This results in mode shapes for which the transverse displacement at any point along the string depends on a sine function, $$ \sin\Big(\frac{n\pi}{L}x\Big)\ , $$ where $L$ is the length of the string, and $n$ is an integer. The animation below shows the first four allowed mode shapes for a fixed-fixed string. The number of "humps" (antinodes) corresponds to the value of $n$.

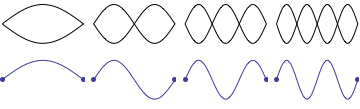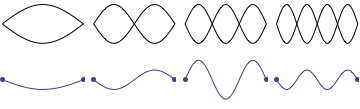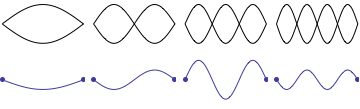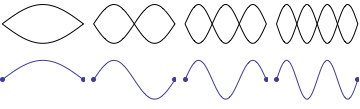
After applying the boundary conditions, the complete expression for the transverse displacement of the string, as a function of time and postion along the string's length, is $$ y(x,t) = \sum_{n=1}^N \big [A_n\cos(\omega_n t) + B_n\sin(\omega_n t)\big ] \sin\Big(\frac{n\pi}{L}x\Big) $$ where $\omega_n$ is the natural frequency of the $n$^th mode, and the coefficients $A_n$ and $B_n$ are determined from the initial conditions.

The string has a linear density $\rho_L$ [kg/m] and is stretched to a tension $T$; transverse waves travel along the string with a speed $c=\sqrt{T/\rho_L}$. The natural frequencies corresponding to the allowed mode shapes depend on the wave speed and the string length, $$ \omega_n = 2\pi\, \frac{n c}{2 L} \ .$$ The natural frequencies will be higher if the string is shorter, or if the tension is higher, or if the density is lower. The natural (or allowed) frequencies are integer multiples of the fundamental ($n=1$) frequency.

Initial Conditions for the Plucked String

In order to determine values for the coefficients $A_n$ and $B_n$ we need to know the initial shape of the string at time $t=0$. These coefficients (called Fourier coefficients) are determined from the initial displacement and the initial velocity of the string, with $A_n$ coming from the initial displacement and $B_n$ from the initial velocity, $$ A_n = \frac{2}{L}\int_0^L y(x,0) \sin\bigg(\frac{n\pi}{L}\,x\bigg) \, dx \ , $$ $$ B_n = \frac{2}{\omega_n L}\int_0^L u(x,0) \sin\bigg(\frac{n\pi}{L}\,x\bigg) \, dx \ . $$ When a string is plucked, it is pulled aside to a transverse distance $h$ at a distance $d$ from one end, and then released from rest. The initial shape of the string will be triangular comprised of two straight line segments.

Since the plucked string is initially released from rest, the initial velocity is zero, and therefore all of the $B_n=0$. To get the values of the $A_n$ you need a math expression for the initial displacement (two straight lines) $$ y(x,n=)= \begin{cases} h\frac{x}{d} \qquad \text{for} \quad 0 \le x \le d,\\ h\frac{L-x}{L-d} \qquad \text{for} \quad d \le x \le L \end{cases} $$ and then you have to carry out two integrals for $ A_n $, (one for each segment of $x$), which yields the result $$ A_n = \frac{2h}{n^2\pi^2} \frac{L^2}{d(L-d)}\,\sin\Big(\frac{d n \pi}{L}\Big) $$ NOTE: if you use a different math expression for the straight line segments to describe the initial displacement, the resulting expression for $A_n$ will look different, but the behavior of the string will be the same. Looking at expression for $A_n$, we can see that the fundamental ($n=1$) has the largest amplitude, and all higher values of $n$ have much smaller amplitudes. Because of the $\sin\big(\frac{d n \pi}{L}\big)$ term, the coefficients $A_n$ will be zero when $n$ is an integer multiple of $L/d$. This means that for a string plucked at a point 1/3 of its length from the end (so that $d=L/3$) all of coefficients $A_3, A_6, A_9, A_{12}$, etc. will be zero and sill be missing from the total sum. Once the coefficients $A_n$ and $B_n$ are known, we can use them to reconstruct the initial shape the string. For the plucked string, with $B_n=0$ and the $A_n$ from the expression above, we have $$y(x) = \sum_{n=1}^N A_n \sin\Big(\frac{n\pi}{L}x\Big) \ . $$ The animation below shows how, as each successive mode $n$ is added to the sum, the shape of the sum of the individual allowed mode shapes begins to look more and more like the initial plucked displacement of the string.

Motion of the Plucked String

The complete Fourier Series expression for the motion of the plucked string is then $$y(x,t) = \sum_{n=1}^N \Big [\frac{2h}{n^2\pi^2} \frac{L^2}{d(L-d)}\,\sin\Big(\frac{d n \pi}{L}\Big)\Big ]\ \sin\Big(\frac{n\pi}{L}x\Big) \cos\Big(2\pi\frac{n c}{2 L} t\Big) \ . $$ When the string is released from rest, each of the allowed modes begins oscillate at its own individual natural frequency, with the result that the sum changes with time as the individual modes combine together. This is illustrated in the animation below, where the thick black curve represents the actual string (the sum of all of the individual modes) and the colors represent the individual modes each oscillating at their own natural frequencies and with their own maximum amplitudes. The frequency associated with the total (sum) string motion is the same as the frequency of the fundamental mode; a guitar string tuned to 384Hz will undergo one complete back and forth motion 384 times every second.

The resulting motion of a string plucked at a different point may be obtained by changing the pluck point $d$ and recalculating the sum.

The shape of the plucked string, in the animation above, follows an envelope formed by the parallelogram formed by the initial shape and its flipped, mirrored image. To confirm that this is actually how a plucked string behaves, the animation below is a high speed video clip from a video on my YouTube channel and it shows that a plucked string does indeed follow this shape as it oscillates upon being released from rest.^[1]

An Alternate Approach -- d'Alembert's Construction

The differential equation of motion that describes the behavior of waves was first derived and solved by d'Alembert in 1717. He derived the differential equation of motion for waves (henceforth called the "wave equation"), $$ \frac{\partial^2 y}{\partial x^2} - \frac{1}{c^2}\frac{\partial^2 y}{\partial t^2} = 0 \ ,$$ and showed that its solutions take the form of the sum of two wave functions traveling in opposite directions, $$ y(x,t) = f(x - ct) + g(x+ct) \ . $$ This idea may be used as an alternate way of explaining the motion of the plucked string without having to resort to Fourier Coefficients and series. The animation below shows that the superposition of two triangle waves, one moving right and the other moving left, will add up to produce the same resulting net string motion.

This may be done for other plucked points as well; the animations below show the d'Alembert solutions for a string plucked at the midpoint and closer to the right end.

Motion of a Specific Point on a Plucked String.

Knowing what the motion of a plucked string looks like, we can answer one more question: What time signal would a guitar pickup record when a string is plucked?^[2] Predicting the time behavior of a specific location on the string, as a function of time, is as simple as plotting the displacement equation $$ y(x,t) = \sum_{n=1}^N \Big [\frac{2h}{n^2\pi^2} \frac{L^2}{d(L-d)}\,\sin\Big(\frac{d n \pi}{L}\Big)\Big ]\,\sin\Big(\frac{n\pi}{L}x\Big) \cos\Big(2\pi\frac{n c}{2 L}t\Big) \ , $$ as a function of time, for a fixed value of $x$. The animation below illustrates what this time signal would look like as the string is vibrating -- the time history on the right shows the position, as a function of time of the dot near the left end of the plucked string. The point actually sits still, at rest (but below its equilibrium position), until the wave envelope reflects from the other end and then the point quickly jumps up and back down again.

This theoretical prediction is also backed up by experimental data. The figure below shows the time signal measured by an optical photogate transducer that measures the postion of a point on the string as it vibrates after being plucked.^[2] The measured data has some small ripples just before the big jumps -- these little ripples are evidence of dispersion due to the stiffness of the string, which causes the speed of waves on the string to become dependent on frequency.

NOTES

I feel obligated to mention that the wobbly string wave motion shown in many "slow-motion" videos on YouTube does not represent the actual string motion, but is an artifact of the rolling shutter effect common to cell-phone cameras.
I'm in the process of writing up a paper about the physics of guitar pickups that compares theoretical and measured time signals and frequency spectra for optical pickupts (which measure string displacement), magnetic pickups (which measure string velocity) and force pickups (which measure the force at the end of the string where it connects to tthe body of the guitar). I'll post a link to the paper here when it has been submitted.