Oscillation of a "Simple" Pendulum
The Equation of Motion
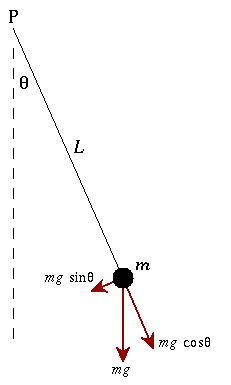A simple pendulum consists of a ball (point-mass) \( m \) hanging from a (massless) string of length \( L \)and fixed at a pivot point \( P \). When displaced to an initial angle and released, the pendulum will swing back and forth with periodic motion. By applying Newton's secont law for rotational systems, the equation of motion for the pendulum may be obtained
equation of simple harmonic motion
\[
\tau = I \alpha \qquad \Rightarrow \qquad -mg \sin\theta\; L = mL^2 \; \frac{d^2\theta}{dt^2}
\]
and rearranged as
equation of simple harmonic motion
\[
\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin\theta = 0
\]
If the amplitude of angular displacement is small enough, so the small angle approximation ($\sin\theta\approx\theta$) holds true, then the equation of motion reduces to the equation of simple harmonic motion
\[
\frac{d^2\theta}{dt^2} + \frac{g}{L}\theta = 0
\]
The simple harmonic solution is
\[
\theta(t) = \theta_o \cos(\omega t) \ ,
\]
where \(\theta_o\) is the initial angular displacement, and \(\omega = \sqrt{g/L}\) the natural frequency of the motion. The period of this sytem (time for one oscillation) is
\[
T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{L}{g}} .
\]
Small Angle Assumption and Simple Harmonic Motion
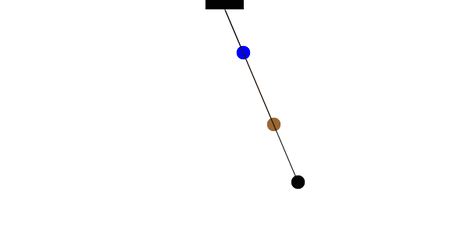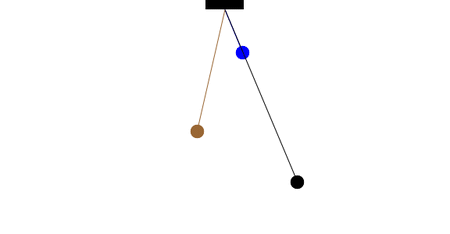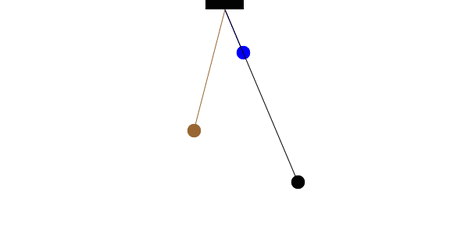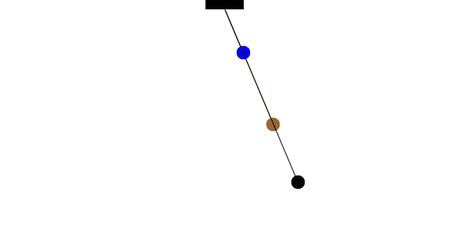The period of a pendulum does not depend on the mass of the ball, but only on the length of the string. Two pendula with different masses but the same length will have the same period. Two pendula with different lengths will different periods; the pendulum with the longer string will have the longer period.
How many complete oscillations do the blue and brown pendula complete in the time for one complete oscillation of the longer (black) pendulum?
From this information and the definition of the period for a simple pendulum, what is the ratio of lengths for the three pendula?
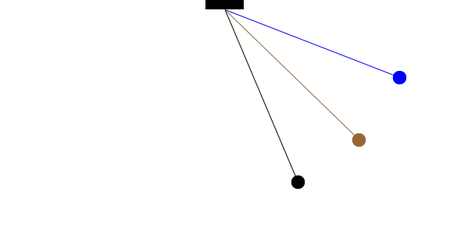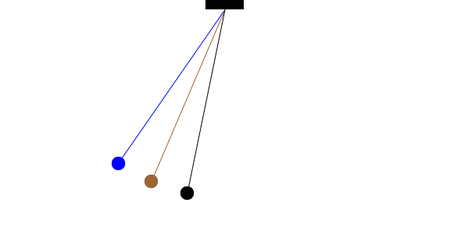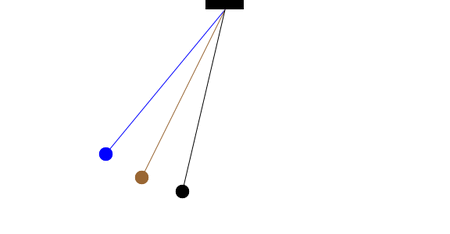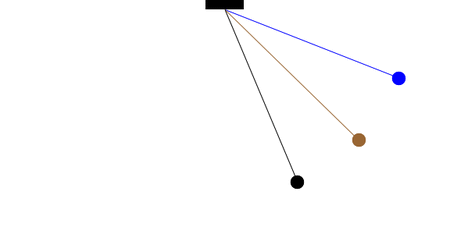With the assumption of small angles, the frequency and period of the pendulum are independent of the initial angular displacement amplitude. A pendulum will have the same period regardless of its initial angle. This simple approximation is illustrated in the animation at left. All three pendulums cycle through one complete oscillation in the same amount of time, regardless of the initial angle.
The Real (Nonlinear) Simple Pendulum
When the angular displacement amplitude of the pendulum is large enough that the small angle approximation no longer holds, then the equation of motion must remain in its nonlinear form \[ \frac{d^2\theta}{dt^2} + \frac{g}{L}\sin\theta = 0 \; . \] This differential equation does not have a closed form solution, but instead must be solved numerically using a computer. Mathematica numerically solves this differential equation very easily with the built in function NDSolve[ ].
The small angle approximation is valid for initial angular displacements of about 20° or less. If the initial angle is smaller than this amount, then the simple harmonic approximation is sufficient. But, if the angle is larger, then the differences between the small angle approximation and the exact solution quickly become apparent.
In the animation below left, the initial angle is small. The dark blue pendulum is the small angle approximation, and the light blue pendulum (initially hidden behind) is the exact solution. For a small initial angle, it takes a rather large number of oscillations before the difference between the small angle approximation (dark blue) and the exact solution (light blue) begin to noticeable diverge.
In the animation below right, the initial angle is large. The black pendulum is the small angle approximation, and the lighter gray pendulum (initially hidden behind) is the exact solution. For a large initial angle, the difference between the small angle approximation (black) and the exact solution (light gray) becomes apparent almost immediately.
