Plane-Wave Partial-Wave Expansion

One of the important problems in acoustics is the scattering of plane waves from cylindrical and spherical objects. This problem is important for many applications in underwater acoustics, ocean acoustics, and the propagation of sound outdoors. This problem is difficult because a 1-D plane wave is usually expressed in terms of Cartesian coordinates, while the radiation and scatting of sound from cylindrical and spherical objects is most appropriately expressed in terms of cylindrical and spherical coordinates, respectively. The trick to making the problem relatively easy to solve is finding a way to express a 1-D plane wave in terms of the functions (Bessel functions and Legendre polynomials) that are used to describe 2D and 3D waves in cylindrical and spherical coordinates. This is where the partial-wave expansion comes in.

Plane-Wave Partial-Wave Expansion for 3-D Spherical Coordinates

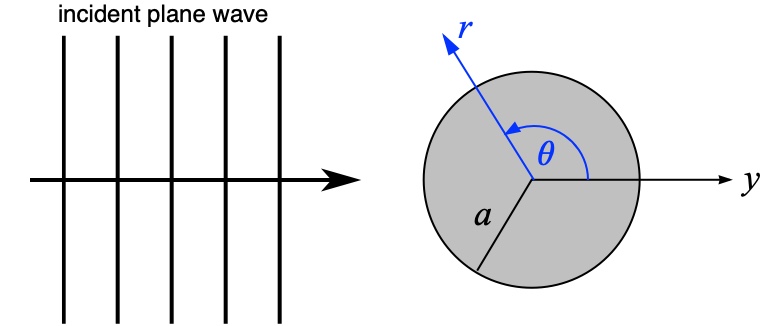
A plane wave traveling with amplitude \(P_{\rm amp}\) is traveling in the positive \(y\) direction toward a spherical object of radius \(a\). Using the geometry of the problem, the plane wave may be written as $$ p = P_{\rm amp} e^{j(\omega t - ky)} = P_{\rm amp} e^{j(\omega t)} e^{-jky)} = P_{\rm amp} e^{j(\omega t)} e^{-jkr\cos\theta} $$ Because Legendre polynomials are orthogonal and form a complete set, they can be used to express any abitrary function of \(\theta\) over interval \([0,\pi]\), so that we can write $$ e^{-jkr\cos\theta} = \sum_{n=0}^\infty A_n P_n(\cos\theta) \ . $$ Using the orthogonality, we can determine that $$ A_n = \Big(\frac{2n+1}{2}\Big) \int_0^\pi e^{-jkr\cos\theta} P_n(\cos\theta)\, \sin\theta\, d\theta = 2\Big(n+\frac{1}{2}\Big)\, (-j)^n\, {\rm j}_n(kr) $$ where \(j=\sqrt{-1}\) and \({\rm j}_n\) is the spherical Bessel function. In order to solve the integral, the term \(e^{-jkr\cos\theta}\) is expanded as a Taylor series and integrated term by term).

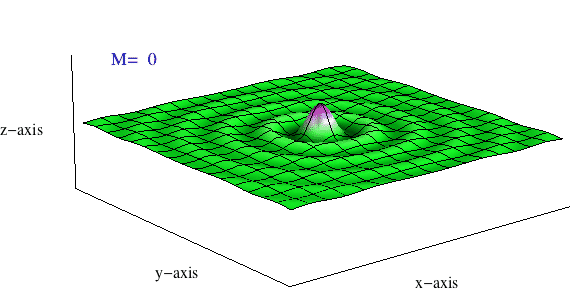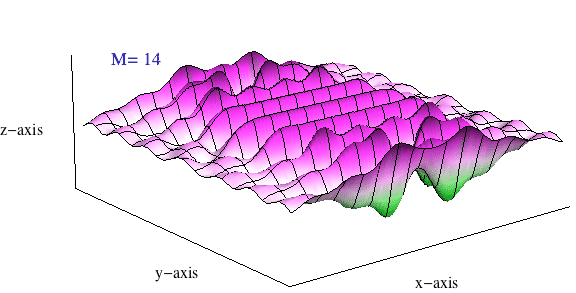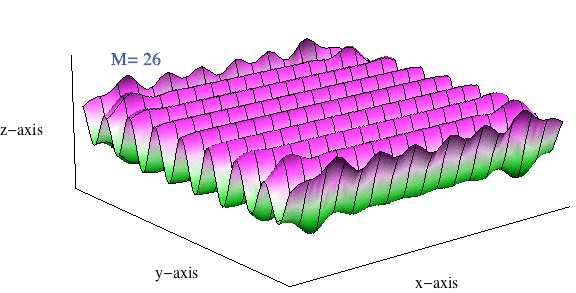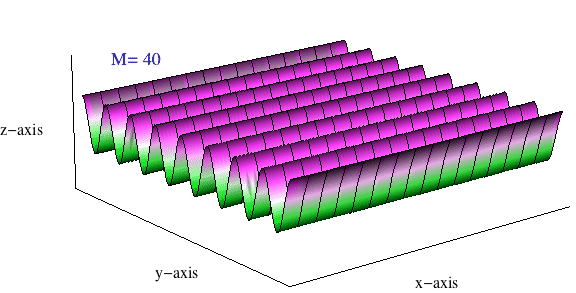
The plane wave may then be written as a 3D plane-wave partial-wave expansion $$ p = P_{\rm amp} e^{j(\omega t)} \sum_{n=0}^\infty (2n+1)(-j)^n\, {\rm j}_n(kr)\, P_n(\cos\theta) $$ The real part of this summation carries the physical meaning, and the sum only includes even terms (\(n=0,2,4,6,\dots\)) The animation at right show a plot of this sum \(\sum_{n=0}^M\) as \(M\) increases from 0 to 40. What starts out as a clearly circular looking function (spherical Bessel function) ends up being a clear plane wave once enough terms have been added to the sum.

Armed with this expression for an incident plane wave written in terms of spherical coordinates, spherical Bessel functions, and Legendre polynomials, the problem of plane-wave scattering from a spherical object may be tackled.

Plane-Wave Partial-Wave Expansion for 2-D Cylindrical Coordinates

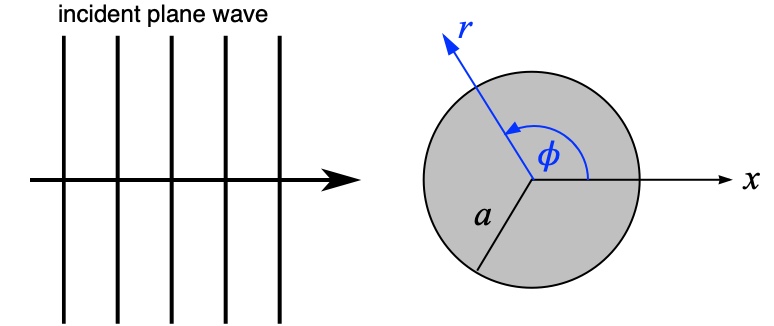
A plane wave traveling with amplitude \(P_{\rm amp}\) is traveling in the positive \(x\) direction toward a spherical object of radius \(a\). Using the geometry of the problem, the plane wave may be written as $$ p = P_{\rm amp} e^{j(\omega t - kx)} = P_{\rm amp} e^{j(\omega t)} e^{-jkx)} = P_{\rm amp} e^{j(\omega t)} e^{-jkr\cos\phi} $$ We can express this incident plane wave in terms of cylindrical functions as, $$ e^{-jkr\cos\phi} = \sum_{m=0}^\infty \epsilon_m (-j)^m \, {\rm J}_m(kr)\cos(m\phi)\ . $$ where \(\epsilon_m=1\) if \(m=0\) and \(\epsilon_m=2\) if \(m>0\).

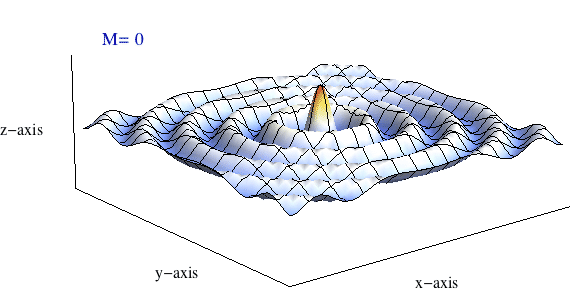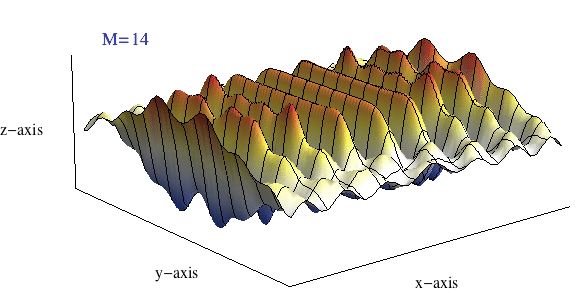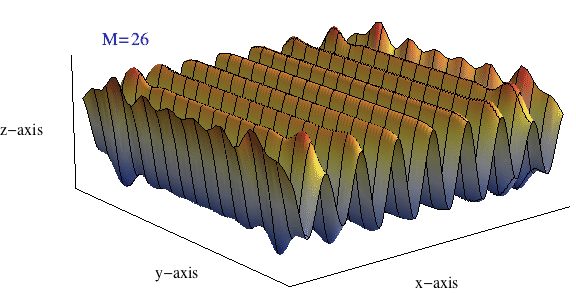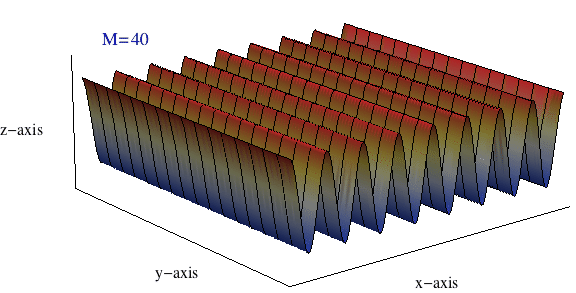
The plane wave may then be written as a 2D plane-wave partial-wave expansion $$ p = P_{\rm amp} e^{j(\omega t)} \sum_{m=0}^\infty \epsilon_m (-j)^m \, {\rm J}_m(kr)\cos(m\phi) $$ The real part of this summation carries the physical meaning, and the sum only includes even terms (\(m=0,2,4,6,\dots\)) The animation at right show a plot of this sum \(\sum_{m=0}^M\) as \(M\) increases from 0 to 40. What starts out as a clearly circular looking ripple pattern ends up being a plane wave once enough terms have been added to the sum.

Armed with this expression for an incident plane wave written in terms of spherical coordinates, spherical Bessel functions, and Legendre polynomials, the problem of plane-wave scattering from a cylindrical object may be tackled.