The Bowed String (Violin)

The motion of the bowed string (violin) is very different from the plucked string (guitar) and the struck string (piano). The plucked and struck strings are both initial condition problems; that is the string is given an initial displacement or velocity, after which the string vibration is a transient with the motion decaying with time. The bowed string is a system driven by a self-sustained friction oscillator. The details of this motion are considerably more complicated than the Fourier Series approach with initial conditions.

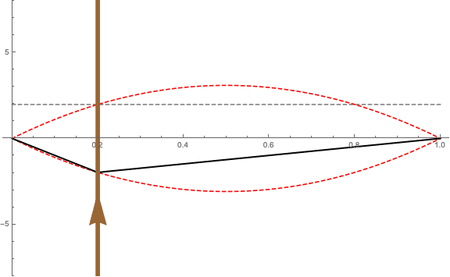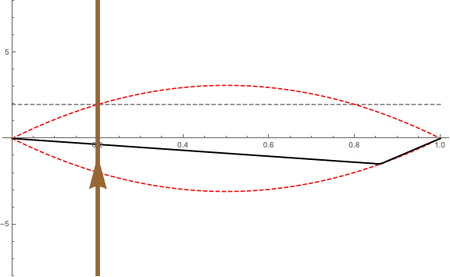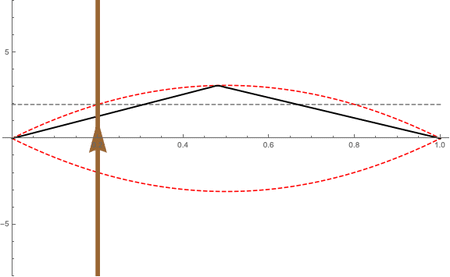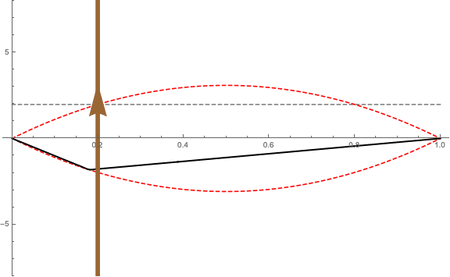The interaction between the bow and the string is called a "stick-slip" mechanism -- the rosin on the bow hair is sticky with a high value of static friction. The bow drags the string along, in the transverse direction, until the restoring force due to the string tension is greater than the static friction, and the string "slips" moving back toward equilibrium in the opposite direction that the bow is moving. The string overshoots its equilbrium and when it reaches its extreme position it is caught and "sticks" to the bow which drags it forward again. As this process repeats itself, the string maintains a triangular shape, with the apex of the triangle racing in a counter-clockwise direction and following an envelope that has the shape of half a sine function. This is illustrated in the animation at right: the brown line with the upwards traveling arrow represents the direction and speed of the bow. The apex of the triangle makes one round trip at the fundamental frequency of the string; if the string is playing an A 440 Hz, the triangle races around in a clockwise direction 440 times per second.

The YouTube video below shows high-speed video of a bowed string; once the bow begins moving, the stick-slip motion of the string is seen, and the triangular pulse begins racing in a counter-clockwise direction.

Video source: ViolinBOW Youtube Channel

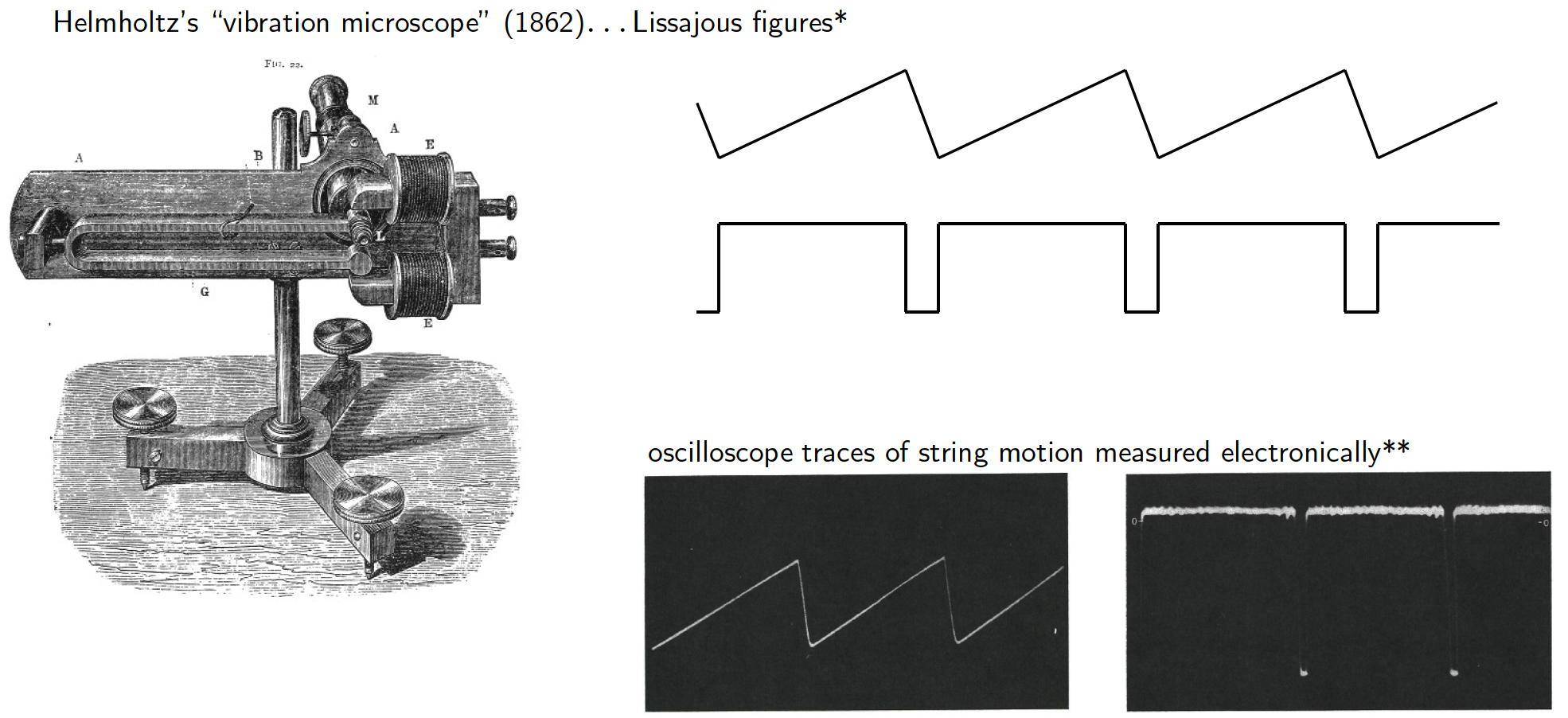The counter-clockwise motion of the string is referred to as Helmholtz Motion because Helmholtz was the first person to observe it in 1862 using his "oscillation microscope" and Lissajous figures.^[1] The figure below shows the "oscillation microscope" that Helmholtz used along with his sketched observations of the motion of a single point on the bowed string; the triangle motion represents the displacement of a point on the string as a function of time, and the rectangular pulses represent the velocity of the same point.^[1] The black photographs are more recent oscilloscope traces of the string motion using an electronic sensor.^[2]

Dependence of Bowed String Motion on Bow Position and Velocity

The mathematical details required to produce an animation of the bowed string are much more complicated than the initial conditions and Fourier coefficients for plucked string or struck string though the resulting string motion may be expressed as a Fourier Series^[3,4] $$ y(x,t) = \frac{2}{\pi^2} \sum_n \frac{1}{n^2}\frac{h\,v_B\,L^2}{(L-x_B)x_B} \sin\Big(\frac{n\pi}{L}x\Big)\sin\Big[\frac{\pi n c}{L}\Big(\frac{x_B}{c}-t\Big)\Big] $$ The movie file at right shows how the Helmholtz string motion depends two important parameters, the bow position $x_B$ and the bow speed $v_B$. Other variables in the equation indicate the string length, L, the speed of waves on the string, c, and the maximum distance the string is pulled by the bow, h.

The movie animation of the equation for the bowed string shows that the amplitude of string's displacement is larger when the bow position $x_B$ is closer to the fixed end. Bowing closer to the bridge will increase the amplitude of the sound, and bowing farther from the bridge (closer to the string's midpoint) will decrease the amplitude. Bowing faster (a larger value of the bow speed $v_B$ increases the resulting string amplitude.

It should be noted, that the speed with which the triangular "kink" races clockwise around the envelope depends only on the fundamental frequency of the string $\Big(2\pi \frac{n c}{2 L}\Big)$; which in turn depends on the string length, tension, and density. The speed of the "kink" trace does not depend on how fast or how hard the string is bowed.

I will note that this model does not account for the bow force, and it does not explain the phenomena of the "wolf" tone that can occur in a bowed string. Those might be topics for a further expansion of this animation page at some point in the future.

NOTES

Hermann L. F. Helmholtz, On the Sensations of Tone, 2nd edition, translated by A. J. Ellis, (reprinted by Dover Publications., 1954), pp. 80-88.

G. Weinreich, "Kopsteg Memorial Lecture (August, 1992): What science knows about violins — and what it does not know," Am. J. Phys., 61(12), 1067-1077 (1993).

J.C. Schelleng, “The Physics of the Bowed String”, Sci. Am., 230(1), 87-95 (1974).

L. Cremer, The Physics of the Violin, transl. by J.S. Allen, (M.I.T. press, 1984).