Modal Analysis of an Electric Guitar

Modal Analysis of an Electric Guitar
Dr. Dan Russell and Paul Pedersen
Applied Physics, Kettering University

The information below provides a layman's description of a student project to study the vibration of a guitar. This is a work in progress, so a couple of the links may not work and the text is not quite as complete (or in depth) as we'd like it to be. But we hope you find some useful information here.
Last updated: January 29, 1999
The images and animations on this page are Copyrighted © 1998 Daniel A. Russell, Ph.D, Science and Mathematics Department, Kettering University, Flint, MI, USA

The Guitar: Epiphone Coronet

The guitar used for this experiment is an Epiphone Coronet electric guitar. This guitar (in addition to an Epiphone amplifier, an ES-335 hollowbody electric, a 1960's Hummingbird acoustic, and two Slingerland drums) was donated to Kettering University by Gibson Musical Instruments Inc for student research projects such as this. The Coronet's body is made of hard maple and our guitar is painted metallic blue. There is a single pickup near the fret board and a humbucker pickup near the bridge. The strings were left attached during the experiment, and the guitar was tuned to its playing frequencies: E₂ (82 Hz), A₂ (110 Hz), D₃ (147 Hz), G₃ (196 Hz), B₃ (247 Hz), and E₄ (330 Hz).

The Experiment: Modal Analysis

The purpose of this experiment was two-fold:

familiarize ourselves with the process of experimental modal analysis, including learning how to use the hardware and software.
to study the vibration of an electric guitar in order to determine its natural frequencies and mode shapes.

More information will be forthcoming concerning experimental modal analysis. In the mean time, the following link provides a nice, although not entirely correct, introduction to the basic concepts involved in a modal analysis study of a vibrating object.

Modal Analysis: A Simple Viewpoint - written by Pete Avitable, University of Lowell, MA

Collecting the Data

In order to allow the guitar to vibrate freely, it was suspended with rubberbands at four points: at both strap connectors and at the base and free end of the neck. Rubberbands seem to work very well for supporting a structure without damping its vibration or adding undesirable boundary conditions.
In order to excite the guitar into vibration, it was lightly struck with a PCB modally tuned hammer force hammer. A small (1 gram) PCB 232B11 accelerometer was attached to the smaller "wing" on the guitar body. This location seemed to allow the accelerometer to respond to the largest number of vibrational modes, and seemed least likely to fall along a node (point or line on the structure which does not move at a particular resonance frequency).
The outputs of the force transducer in the hammer tip and the accelerometer were fed into their respective power supplies, and then into a HP 35670A FFT analyzer. We measured the Frequency Response Function (a transfer function) which took the ratio of output acceleration to input force. For this preliminary experiment we limited the frequency range of our measurements to 0-400 Hz. We found that beyond 400 Hz the coherence between input force and output acceleration degraded quickly and the frequency response functions became very noisy. In the future we may investigate with different hammer tips to see if we can extend the frequency range of our analysis.
We used the method of fixed response modal analysis, in which the accelerometer is fixed at one location, and the force hammer is moved over the entire surface of the structure. We identified 148 measurement points on the guitar. At each point Paul lightly hit the guitar with the hammer and took the average of three good hits to obtain the frequency response function for each point.
example FRF plot

Post-Processing the Data

Post processing of the frequency response functions was performed using the modal analysis software STAR Modal from Spectral Dynamics. By looking at the frequency response functions we were able to identify at least 5 prominent peaks which represented modes of vibration. We placed a narrow frequency band around each peak and used a quadrature fit to curve fit the data. We have found that polynomial fits provide slightly more accurate frequency information, but that quadrature fits provide better looking (cleaner) mode shapes. After the computer had finished processing the data we were able to view animations of the five mode shapes we had identified.

The Results: Modes of Vibration

The animated GIF movies below show the first five modes of vibration for the Epiphone Coronet electric guitar. In all cases the amplitude of vibration is greatly exaggerated for effect in showing the movies. The guitar does not really vibrate with such large amplitudes. Click on each movie to download a larger version.

	Mode #1 The first mode of vibration occurs at 55.3 Hz, and appears to be a simple bending mode. The entire guitar behaves much like a free-free beam vibrating in its fundamental mode. There are two nodal lines (places where the guitar does not move) - one is near the free end of the neck, and the other is close to the middle of the body.
	Mode #2 The second mode of vibration occurs at 160.1 Hz, and looks like the second free-free bending mode. Again there is a close similarity to the second mode of a free-free beam.
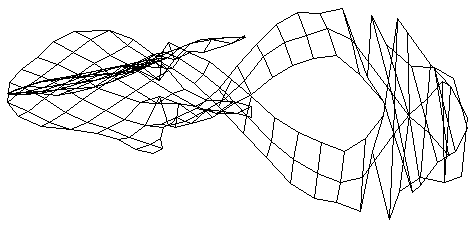	Mode #3 The third mode of vibration occurs at 189.4 Hz, and appears to be a combination of bending and twisting motions. (Animated GIF is not yet available) The body oscillates in a bending fashion like it does in modes 1 and 2, but the neck appears to twist as it bends.
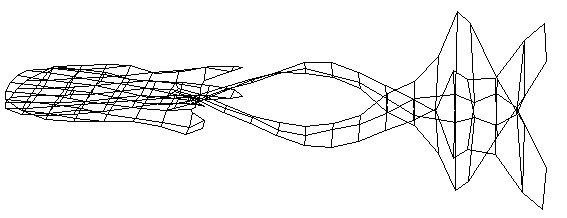	Mode #4 The fourth mode of vibration occurs at 300.5 Hz, and appears to be a combination of bending and twisting motions. (Animated GIF is not yet available) The body oscillates in a bending fashion like it does in modes 1 and 2, but the neck appears to twist as it bends.
	Mode #5 The fifth mode of vibration occurs at 369.74 Hz Hz, and is a torsional mode. This is most clearly seen in the vibration of the body - opposite corners move together in phase as if the body were twisting. Nodal lines roughly split the body into four equal parts. The neck exhibits both bending and twisting motions.

Back to Dr. Russell's Guitar Research Page