Nonlinear Models of Baseballs and Softballs

What's inside a baseball?

One of the things that makes modelling the bat-ball collision difficult to model is the fact that the ball behaves as a nonlinear spring, primarily because of the way a baseball is made. The figure at right shows a cross section of a major league baseball.[1,2] At the very center of the ball is a small, grape-sized cork sphere, surrounded by a two layers of rubber, the inner layer being black and the outer layer red. If dropped on the floor, this core bounces much like a superball. Surrounding this inner core are several layers of tightly wound yarn - the innermost and thickest layer is dark yarn, followed by thin layer of white yarn and an outer layer of dark yarn. Winding these layers more or less tightly affects the elasticity of the ball; the tighter the winding, the livelier the ball.* Covering these layers of yarn is a thin layer of tweed, and finally the outer leather cover. The construction of a modern softball is less complicated. A modern softbal basically consists of either a cork or rubber core surrounded by a leather skin. 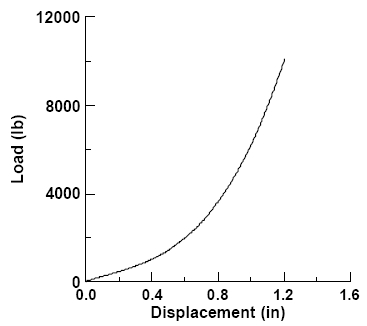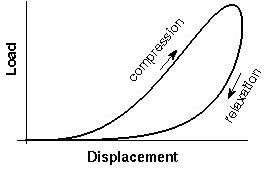In attempting to develop a model that correctly captures the essential phyiscs behind the trampoline effect in a hollow bat, at least to a first order approximation, the ball may be treated as a single degree of freedom mass-spring system. The mass of the ball is just the total mass of the actual ball. To determine the spring constant, or stiffness, and the damping constant for the ball we must first learn more about its nonlinear behavior. * In the summer of 2004 I had the opportunity to partipate in an experiment comparing a dozen unused Rawlings MLB baseballs from the 1970's with a dozen baseballs made in 2004. We wanted to see if we could find any evidence that modern baseballs were "juiced" compared with older baseballs. We fired the baseballs from an air cannon at 120mph towards a rigid surface and measured the coefficient-of-restitution. We found no statistical difference between the two sets of balls.[3]

Cross-section slice of a baseball.

Nonlinear Force-Compression Curves Evidence of the nonlinear properties of a baseball may be observed by attempting to squish a baseball in a press and measuring the amount of force required to compress the ball a given distance. The figures at right show a MLB baseball being compressed in a static compression test, along with the resulting force versus compression curve. If the ball behaved as a linear spring, then the force F and compression x would be related by Hooke's law F= k x and a graph of force (load) versus compression (displacement) would be a straight line. In order to compress the ball twice as much you would need to apply twice as much force. But, a baseball is not a linear spring. Instead, the relationship between force and compression is a power law F= k xp and a measurement of force (load) versus compression (displacement) would result in a curve like the plot shown at right. This nonlinearity means that a baseball becomes stiffer the more you try to compress it. In order to compress the ball twice as much you might need three times the force. Several researchers[4-6] have published static compression results from which is it possible to estimate the effective spring constant k and the degree of nonlinearity p necessary to adequately describe the behavior of a softball or baseball using a simple mass-spring model.

Hysteresis Loops

An additional complication in modelling the nonlinearity of the ball arises from the fact that the force-compression curve followed while the ball is being compressed is not the same as when the force is removed and the ball relaxes and expands. The ball takes more time to expand then it does to compress. Mathematically, this means that the exponent p in the equation   F= k xp     is different during compression than it is during relaxation. This is due to frictional forces within the material inside the ball. Graphically, this means that the ball will trace out a hysteresis curve (as shown at right) while the ball is being compressing and relaxing. Physically, the area contained inside the hysteresis curve represents the amount of energy that is lost to internal friction forces. In my attempt to model the hysteresis of the baseball (or softball) I have adapted a hysteresis model originally developed for analysing the nonlinear behavior of piano hammer felt.[7]

Coefficient of Restitution depends on ball speed

One final layer of complexity is the fact that the shape of the hysteresis curve and the degree of nonlinearity depends upon the speed with which the applied force changes. The graphs shown above are typical of what one would find for a "static" compression test in which a force is applied, the system is allowed to settle briefly and the displacement is measured before the force is changed. A static compression test of a ball can take several minutes to conduct. In a dynamic test, a ball is fired at high speed towards a rigid wall, and the impact duration is usually on the order of a millesecond. Such high-speed dynamic impact tests are used to measure the coefficient of restitution (COR) of softballs and baseballs. The plot at right shows data for three baseballs and a softball which were shot at various speeds towards the barrel of a baseball bat. The barrel of the bat was fixed at each end so that is could not move, though it was able to compress during the impact with the ball. The COR of the balls was measured by taking the ratio of the rebound speed to the incoming speed. The data shows that as pitch speed of the ball increases the COR values decrease. Data obtained from firing balls at a rigid wall show a very similar behavior. Not only does the COR drop with increased speed, but the shape of the hysteresis curve changes, and the duration of the contact time between the ball and the object it strikes also decreases with increasing ball speed.

COR versus Compression

When you pick up a softball you will usually find two numbers printed on the ball as ratio, something like 375/.44. These two numbers represent the compression and Coefficient-of-Restitution (COR), respectively. The compression is simply the amount of force in pounds that is required to compress the ball a quarter of an inch, and it represents the "hardness" of the ball. Compression is measured by performing a static compression test on the ball. A compression value of 375 means that if 375-lbs of force were applied to the ball it would compress by 0.25-inches. If you held a 375/.44 softball in your hand tried to squeeze it as hard as you can, and then try the same thing with a 575/.44 ball, the 575 ball would feel harder because 200 more pounds of force are required to compress the ball the same amount. The second number stands for the coefficient-of-restitution, or COR, and represents the elasticity or springiness of the ball. The COR is measured by firing a ball from an air cannon at 60-mph (or 90-mph) towards a rigid surface and measuring the ratio of rebound speed to initial speed. You could compare two balls by dropping them from the same height onto a flat cement floor. If you compared a 375/.47 ball with a 375/.40 ball you would find that the .47 COR ball would bounce slightly higher.

Recently, several bat manufacturers and some scientists have suggested that a better (and safer) way to control the game would be to regulate the balls used in a game (ie, choosing a deader or softer ball) instead of banning bats as is the current practice.

Summary of Nonlinear Behaviors Needed to Correctly Model the Ball

1. The stiffness of the ball model must behave like a hardening spring, becoming stiffer as more force is applied.
2. The nonlinear stiffness must be different for the compression and relaxation portions of the force-compression cycle.
3. As the speed of the ball increases, both the COR and the contact duration must decrease.
4. The model must accurately predict the effect of changes in stiffness (compression) and elasticity (COR).