Physics of Baseball & Softball Bats

The impact between bat and ball is an extremely violent one, in which the bat imparts a huge force on the ball thereby causing it to change directions and gain speed. The following numbers are consistent with what happens each time a MLB player hits a home run. Consider a baseball with a mass of 5.125 oz (or 0.145 kg) which has an initial velocity of 90mph (40.2 m/s) toward the batter. The contact time between bat and is about 0.7 milliseconds (0.0007 s). After the collision with the bat, the ball reverses direction and travels away from the batter with a velocity of 110mph (49.1 m/s). Using Newton's second law we can estimate the average force acting on the ball during the bat-ball collision: $$ F_{\rm avg}={ m v_f - mv_i \over \triangle t}$$

Plugging in the numbers we find the average force to be F_avg=18,436 N, which is equivalent to an average of 4124 lbs of force during the collision. The impulse delivered by this force is the product of the average force the the contact time, resulting in an impulse of 12.91 Ns.

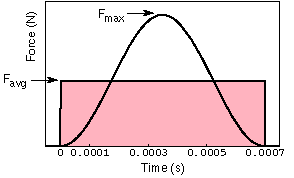
The force that the bat exerts on the ball is not a constant during the entire duration of contact, but instead follows more of a sine-squared time history, starting and ending at zero and peaking approximately half way through the duration of contact. The figure at left illustrates this. The area under a force-vs-time curve is the implulse provided by the force. The average force, calculated above, is the constant force which acts for the same duration as the actual force, and encloses the same area under its force-vs-time curve (providing the same impulse) as does the actual force. Data for force-vs-time curves for a baseball^[3] may be reasonably well fit by a function of the form: $$ F(t) = F_{\rm max}\sin^2(At) $$

where A=4500 to provide a 0.0007s contact time. The impulse (area under the curve) provided by this force may be obtained by integrating this force function over the contact time. We can estimate the peak force by setting this impulse equal to that provided by the average force, calculated above. Doing so results in a peak force of 36,982 N which is equivalent to a peak force of 8314 lbs!

So, during the bat-ball collision, an average force of roughly two tons acts during the 0.7 millisecond contact time, with a peak force of about four tons. That's a lot of force! We can determine the average acceleration experienced by the ball from Newton's second law:  F=m a. Using the numbers above, we obtain an average acceleration of 127,145 m/s², or 12,740 times the acceleration due to gravity!