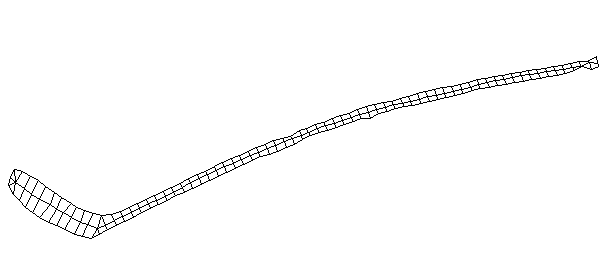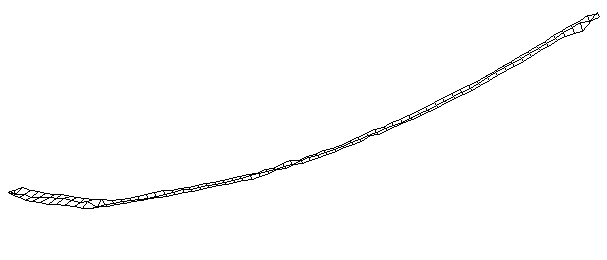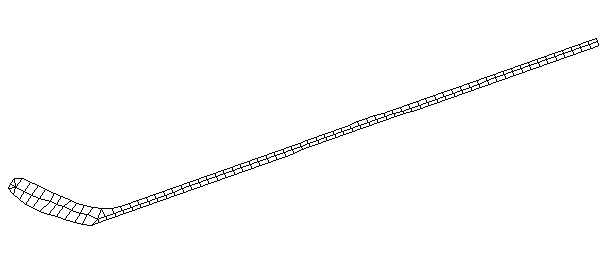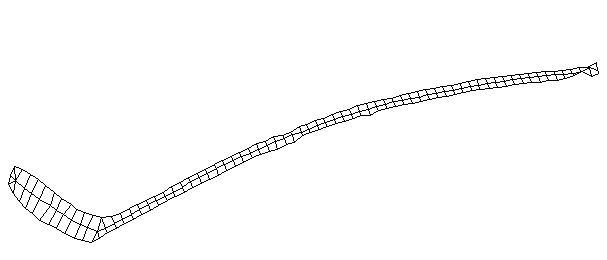
| Bending Mode #1 (56.7 Hz)
This is the first bending mode. The entire stick is bending as a single oscillating structure. Usually the first bending mode of a freely supported beam has two nodes with one major antinode inbetween, and the mode number m is one digit less than the number of nodes (m=n-1). A node is a point on the structure that doesn't oscillate for a particular mode shape. However, because of the blade, the first bending mode of a hockey stick has three nodes with two major antinodes.
It is interesting the the node at the blade is approximately where the impact point with the puck would occur. |

| Torsional Mode #1 (242.5 Hz)
This is the first torsional mode of stick bending mode. Rather than bending, the stick is twisting. In a rectangular beam, teh first torsional mode would have a nodal line down the length of the beam and another across the middle of the beam. However, the hockey stick geometry (blade connected to handle) changes this rule. Instead, the number of nodes n for a torsional mode of a hockey stick appears to be one less than the mode number m. So, the first torsional mode has no nodal lines. |
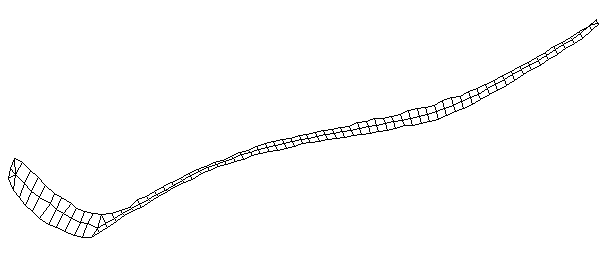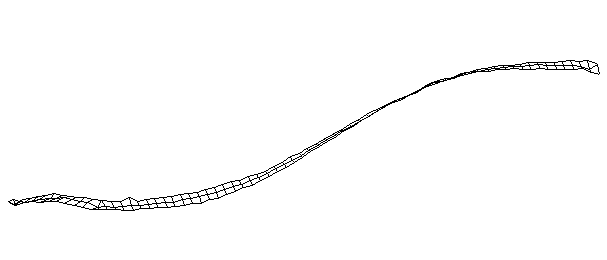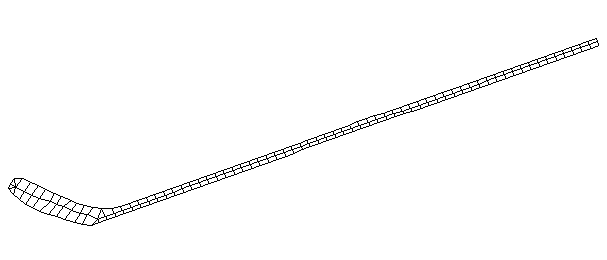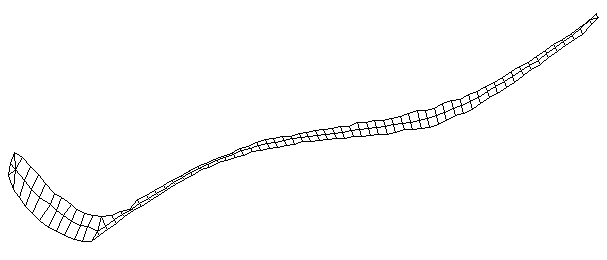
| Bending Mode #2 (157.0 Hz)
This is the second bending mode. There are four nodes, and three antinodes between. |

| Torsional Mode #2 (477.6 Hz)
This is the second torsional mode for the blade. The stick is twisting about its long axis, with a node right about where the blade joins the handle. |
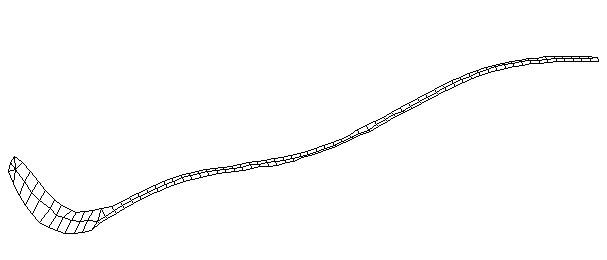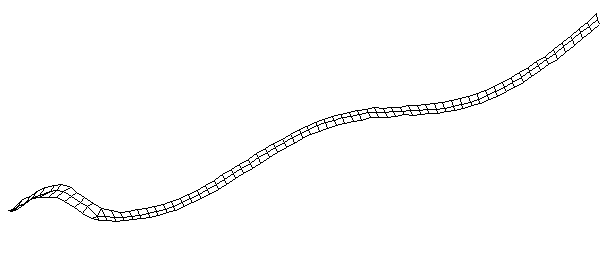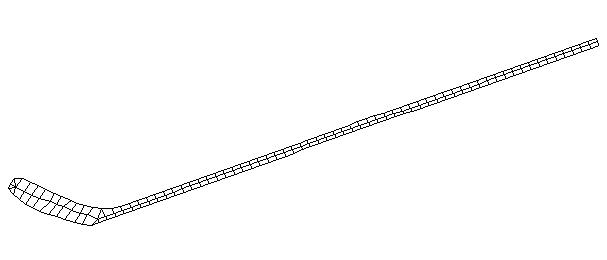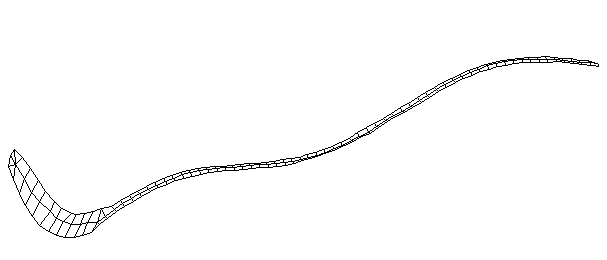
| Bending Mode #3 (281.0 Hz)
This is the third bending mode. There are five nodes and four antinodes. |
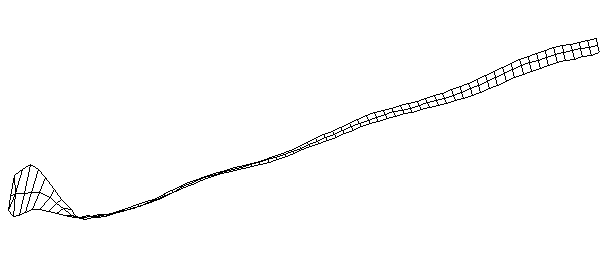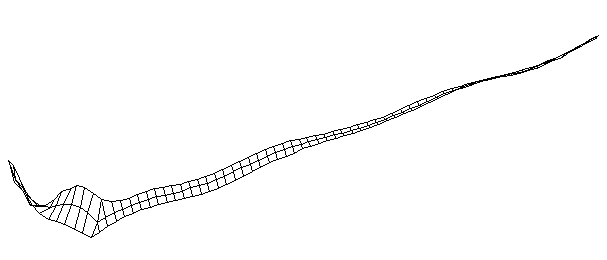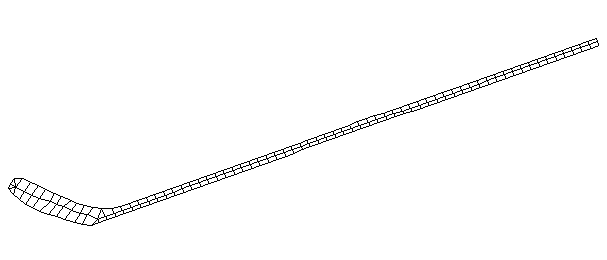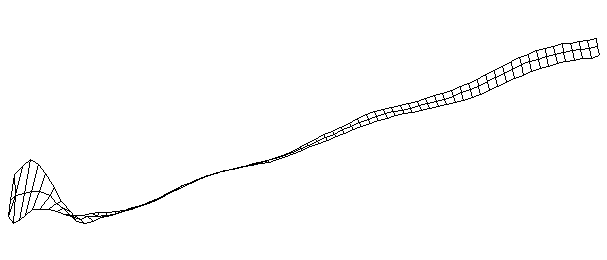
| TorsionalMode #3 (1028.0 Hz)
This is the third torsional mode. There is a node at the middle of the blade and another at the midpoint on the handle. |
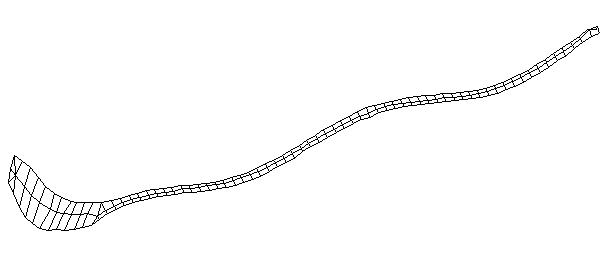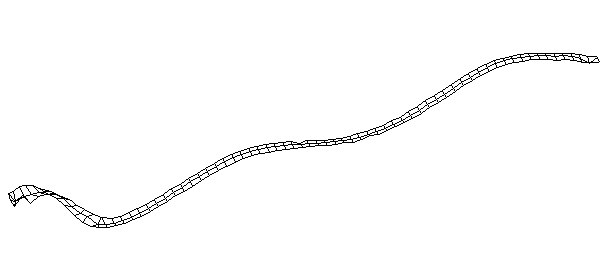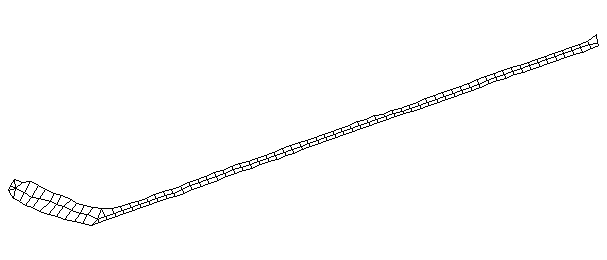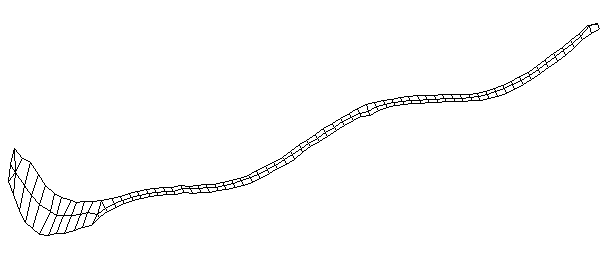
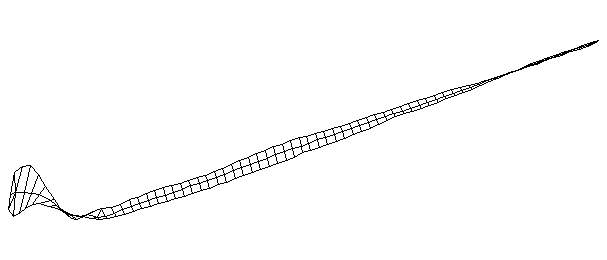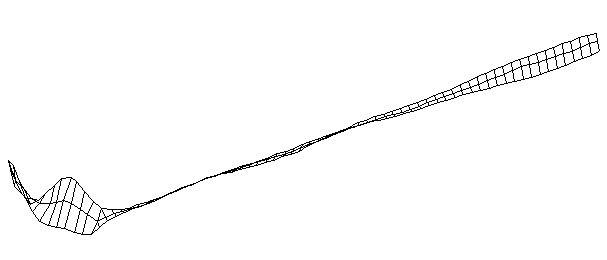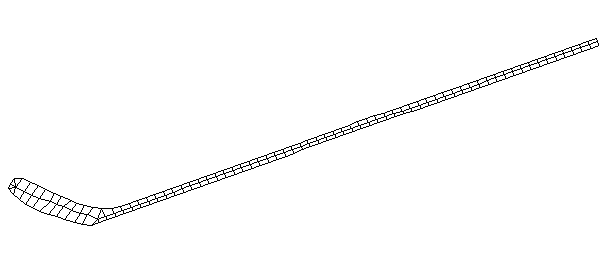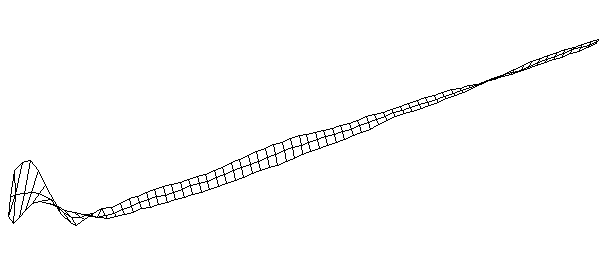
| Bending Mode #4 (420.0 Hz)
This is the fourth bending mode. There are six nodes and five antinodes |
| TorsionalMode #4 (1367.0 Hz)
This is the fourth torsional mode. There is a node at the middle of the blade, another at the junction between blade and handle, and a third node about two-thirds of the length up the handle. |
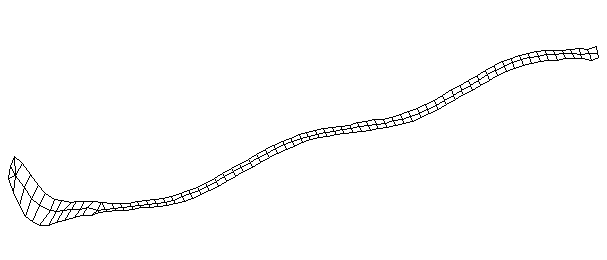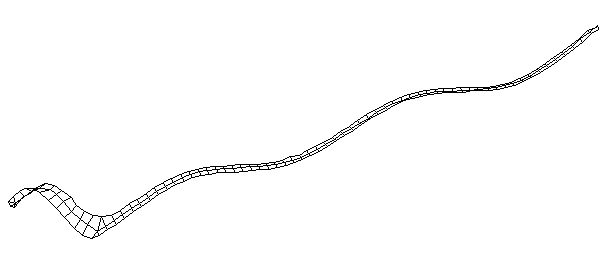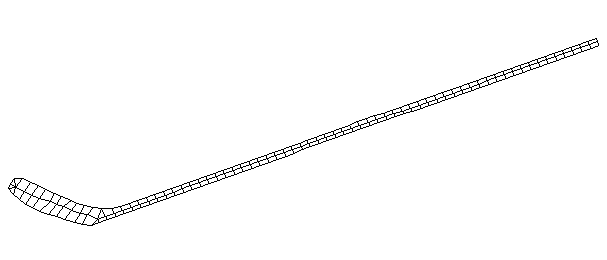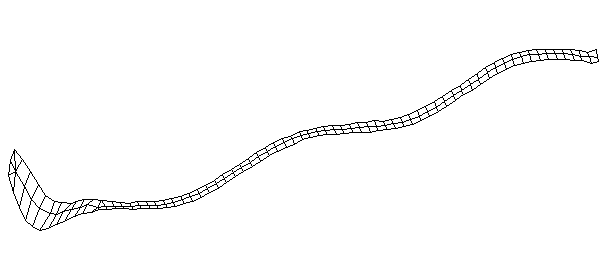
| Bending Mode #5 (571.0 Hz)
This is the fifth bending mode. There are 7 nodes and 6 antinodes. |
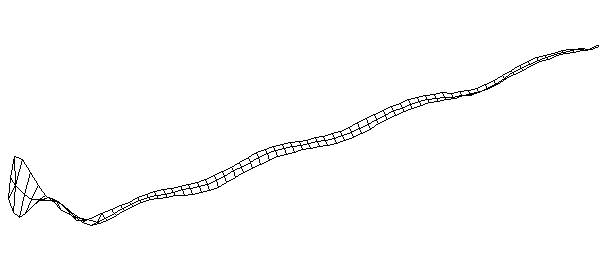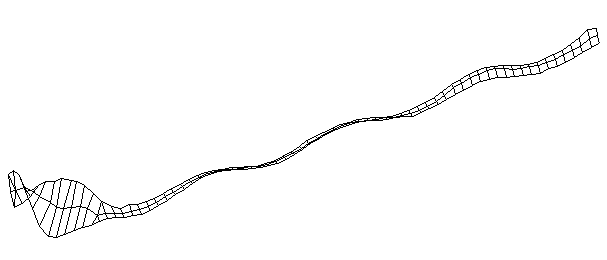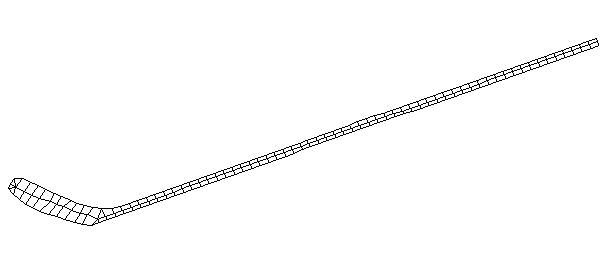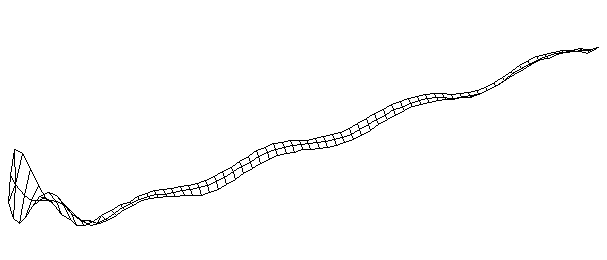
| TorsionalMode #5 (1457.0 Hz)
This is the fifth torsional mode. The frequency of this mode is very close to that of the 9th bending mode, and there appears to be some coupling between the two modes. The handle does not appear to be a clean twising motion, but intead looks like a combination of twisting and bending. |
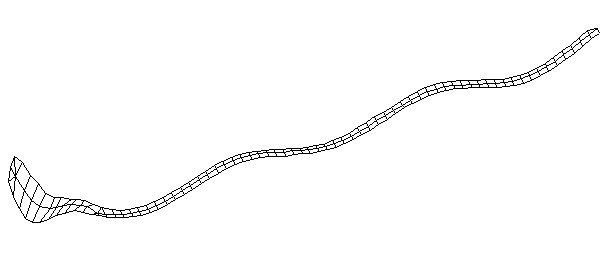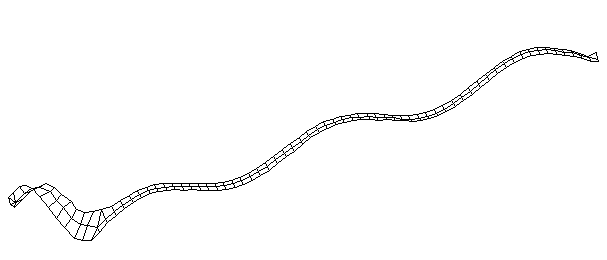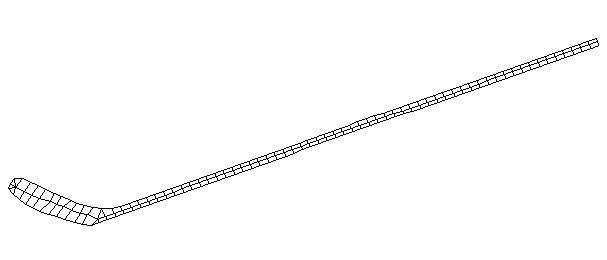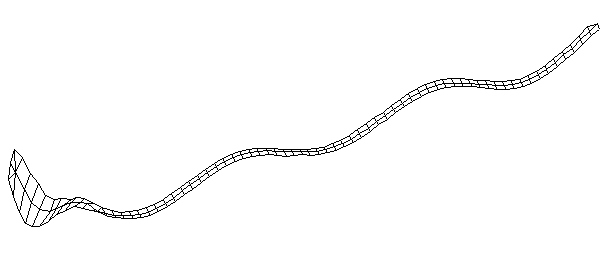
| Bending Mode #6 (744.5 Hz)
This is the sixth bending mode. There are 7 antinodes and 8 nodes. | |
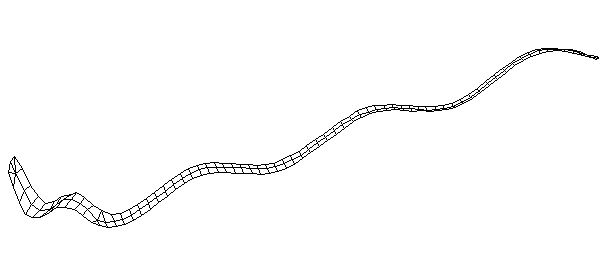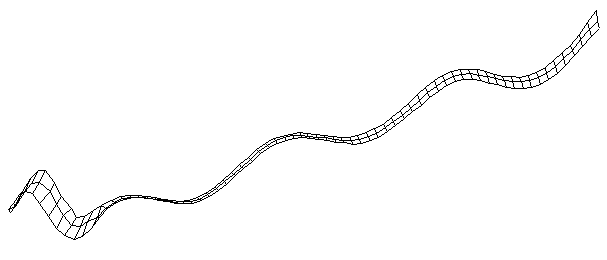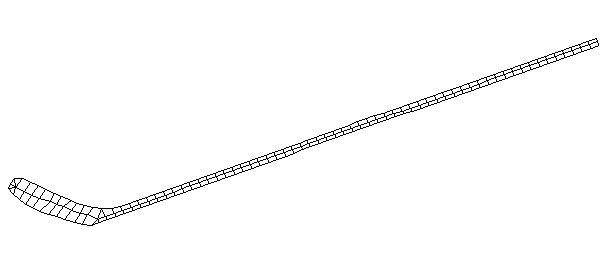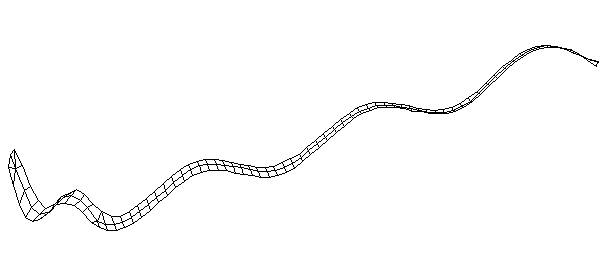
| Bending Mode #7 (961.0 Hz)
This is the seventh bending mode. There are 8 antinodes and 9 nodes. | |
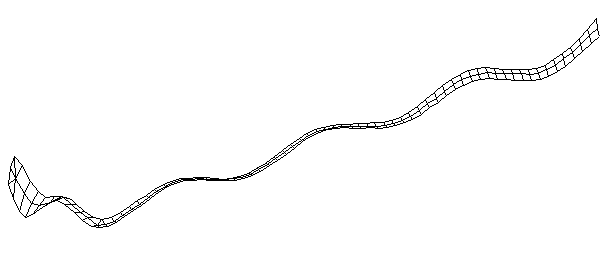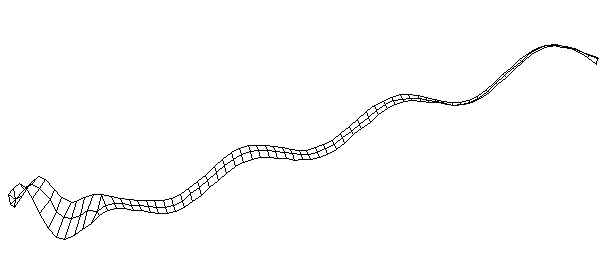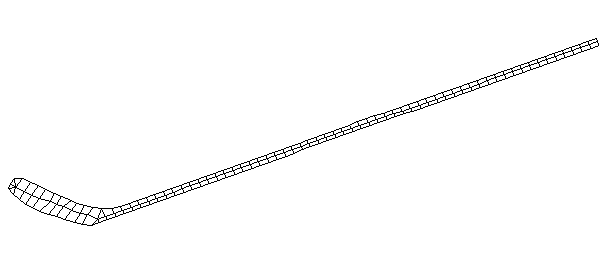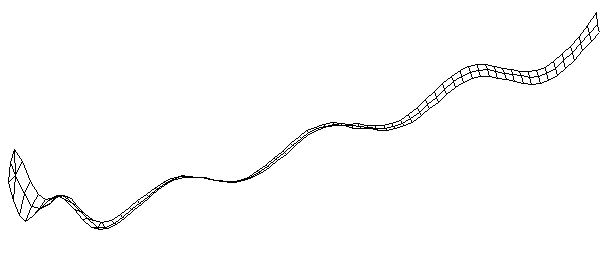
| Bending Mode #8 (1230.0 Hz)
This is the eighth bending mode. | |
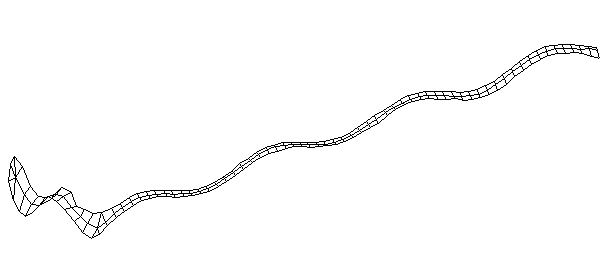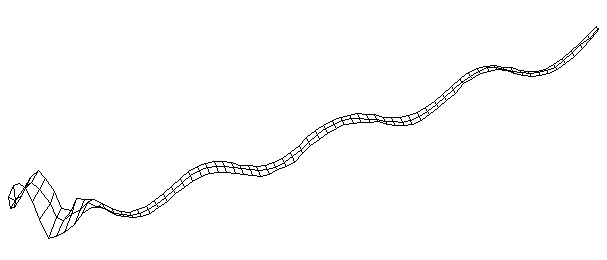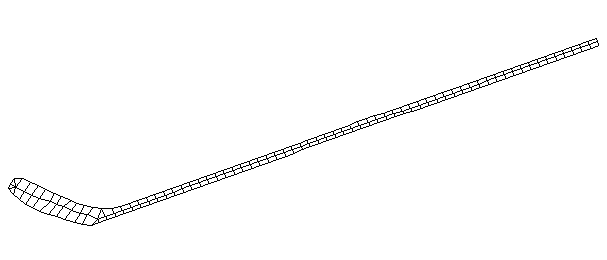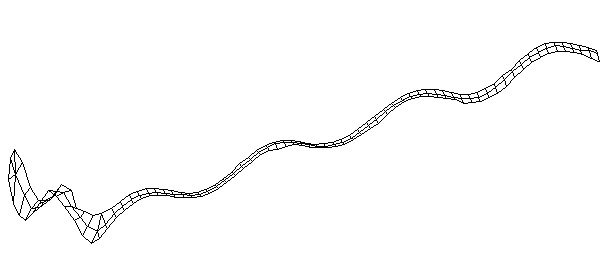
| Bending Mode #9 (1416.0 Hz)
This is the ninth bending mode. | |
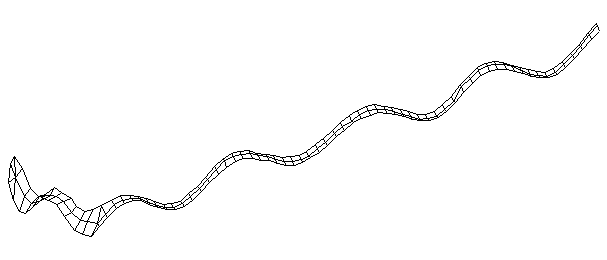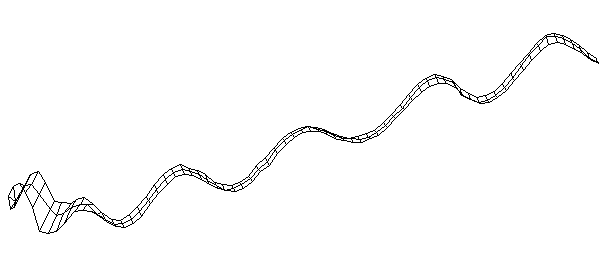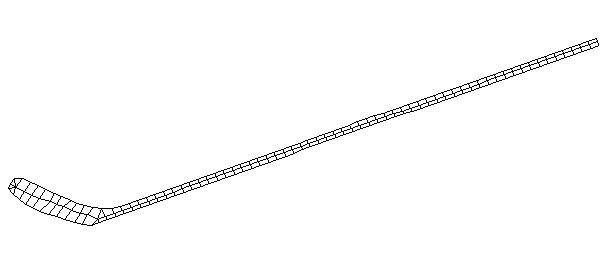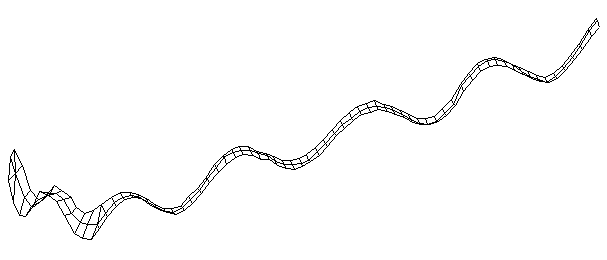
| Bending Mode #10 (1703.0 Hz)
This is the tenth bending mode. | |
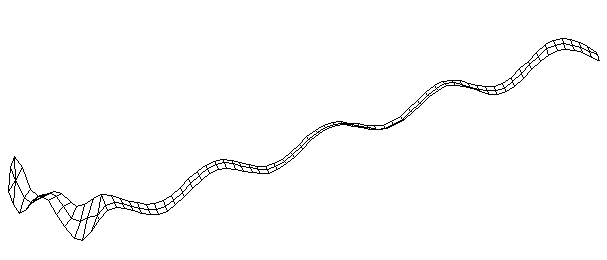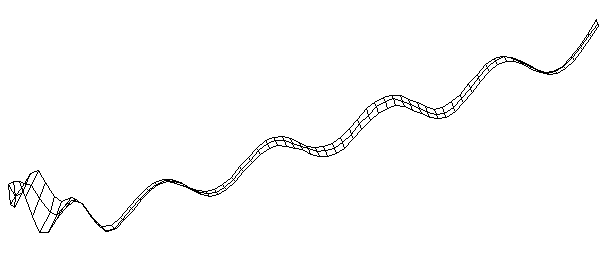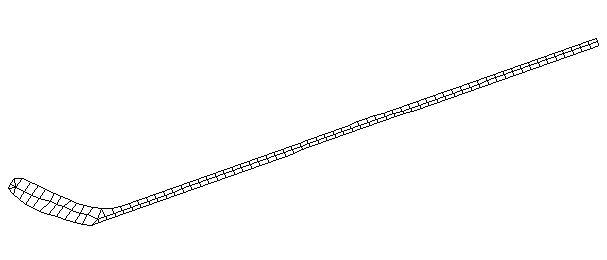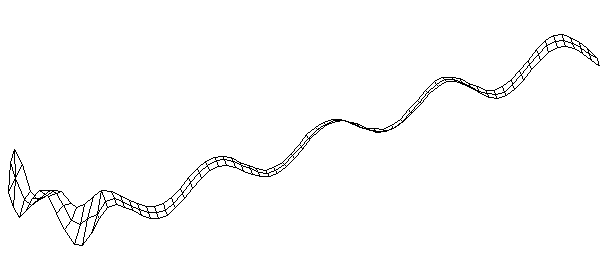
| Bending Mode #11 (2028.0 Hz)
This is the eleventh bending mode. | |


 Experimental Modal Analysis was conducted on a composite hockey stick at the request of Rosanna Anderson, a graduate student in the
Experimental Modal Analysis was conducted on a composite hockey stick at the request of Rosanna Anderson, a graduate student in the 















