|
A freely supported baseball bat exhibits several flexural bending modes of vibrtation which are similar to those of a free-free beam. One might be inclined to believe that a hand-held bat should be treated more like a clamped-free (cantilever) beam. However, research has shown[1] that while the hands quickly damp the bat vibrations, a hand held grip (even tightly gripped) does not significantly change the vibrational frequencies or the modeshapes. The frequencies and shapes for a bat which is free at both ends, sufficiently describe the vibrational behavior of a held bat.
The animations at right show the first four bending modes of a baseball bat. Actually the animations were created from experimental data obtained for a Louisville Slugger Genesis slow pitch softball bat, a hollow barrel bat made from carbon fiber composite materials. However, the vibrational shapes and the node locations are very similar to those for solid wood and aluminum baseball/softball bats I have tested in the acoustics laboratory at Kettering University.
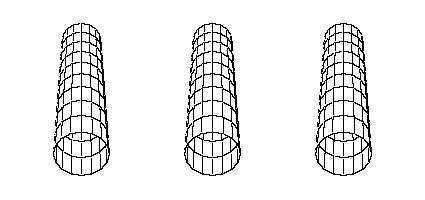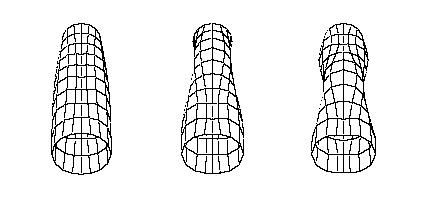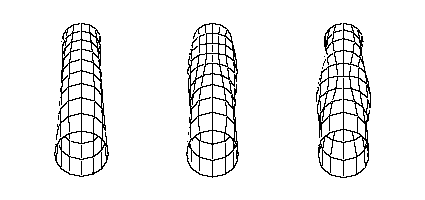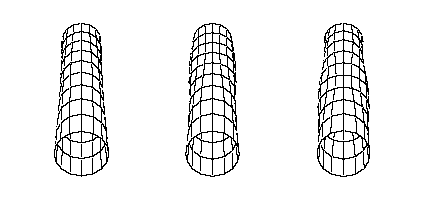
The first bending mode usually occurs at a frequency around 170Hz and is extremely important to the performance of a bat. One of the definitions of the "sweet spot" is the location of the node at the barrel end of the bat. This point, usually 5-7 inches from the barrel end, does not move when the bat is vibrating in its first (or fundamental) bending mode. Another node exists about 6 inches from the handle end (both nodes are identified by the black dots in the animation). An impact at the node will not cause the bat to vibrate, and thus none of the initial energy of the ball will be lost to the bat. In addition, the player will not feel any vibration at this frequency.
The second bending mode, usually occuring near 600Hz, is also very important as it also has a node about 2-3 inches from that of the first bending mode. A "sweet zone" is often defined as the region between the nodes of the first two bending modes.[2] An impact in region will minimally exite the first two bending modes, so the player will feel little vibration and the ball will not lose energy to bat vibration.
The higher bending modes probably have little influence on the feel of the bat, but computer calculations have shown that they can significantly influence the post-impact ball speed.[3,4]
|
First Bending Mode

Second Bending Mode

Third Bending Mode

Fourth Bending Mode

|






 The animation at left shows how the cross-section of the barrel alternately compresses and expands in perpendicular directions. The animations at right show the vibration of the top and bottom of the barrel while viewing the bat from the side.
The animation at left shows how the cross-section of the barrel alternately compresses and expands in perpendicular directions. The animations at right show the vibration of the top and bottom of the barrel while viewing the bat from the side.