Membranes versus Strings: Initial Conditions
The animations on this page were inspired by Figures 40 and 41 in Philip M. Morse, Vibration and Sound, 2nd Ed., (Acoust. Soc. Am., 1981), pp. 184-187.
How is a Membrane different from a String?
In many textbook discussions of vibration and sound, the vibration of an elastic membrane is often presented as simply being a two-dimensional analog of an elastic string. This makes sense, especially when using rectangular coordinates, since the wave equation for membranes looks just like the wave equation for strings (except that is involves a spatial second derivative with respect to two variables). Also, the speed of waves in a membrane depends on the in-plane tension (which provides the restoring force) and the surface mass density (which provides the inertia) in the same way that the speed of transverse waves on a string depends on the tension and linear mass density. Finally, the solutions of the wave equation are sine and cosine functions for both the string and the rectangular membrane. As a result, the standing waves on a rectangular membrane look very similar to standing waves on a string.
For a circular membrane, which requires the use of cylindrical polar coordinates, the wave equation takes of the form of Bessel's equation and the solutions involve cosine and BesselJ functions, so the mathematical analogy is not as clear.
However, when looking at the transient response to initial conditions for a membrane, we can clearly notice several important differences between wave propagation in two-dimensions on the membrane and wave propagation in one-dimension on a string. The animations below show (from left to right) the propagation of waves on an infinite string, the propagation of waves on a 1-D slice of a 2-D membrane, and the propagation of 2-D waves on an infinite membrane. The first set of animations shows the result for an initial displacement and the second set of animations is for an initial velocity.
Initial Displacement (plucked at the center)
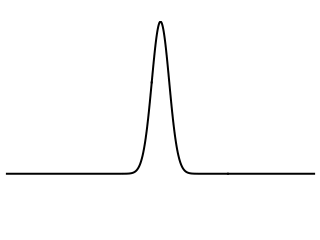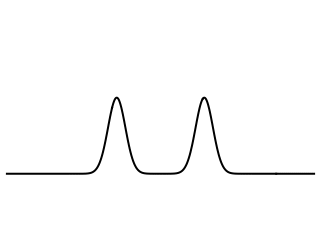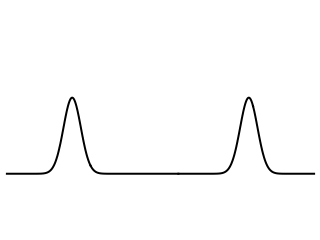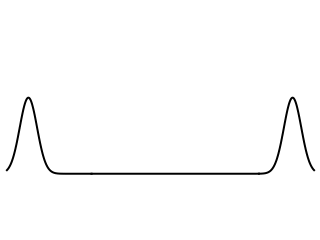
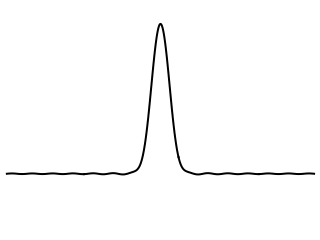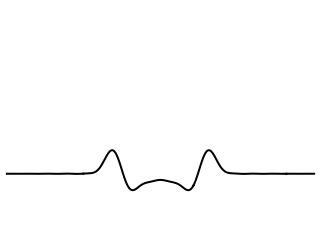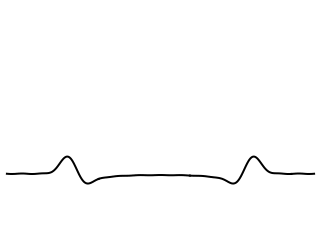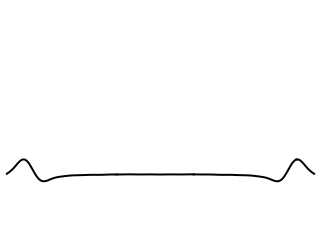
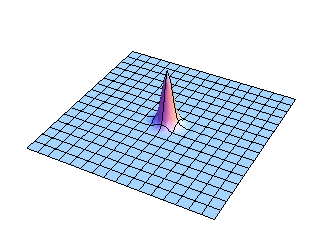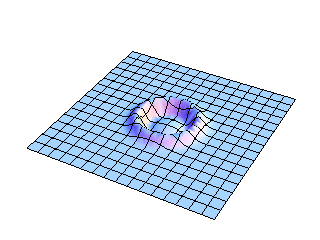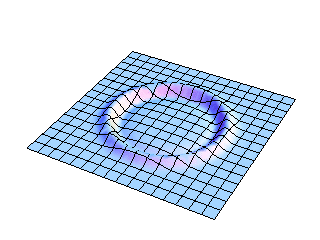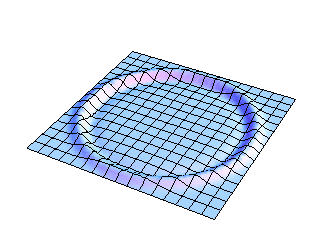
First, let's compare the behavior of strings and membranes in response to an initial displacement. The string or membrane is plucked at the center by giving it an initial displacement in the form of a Gaussian function and releasing the initial displacement from rest.
1-D String
Slice of a 2-D Membrane
2-D Membrane
Waves on a one-dimensional string are a superposition of right-going and left-going waves. So, an initial displacement pulse on a string immediately separates itself into two individual pulses of equal shape and amplitude, one traveling to the right and the other traveling to the left. Both pulses travel with constant speed and maintain a constant shape and amplitude as they travel away from each other along the string. The center of the string returns to its zero equilibrium position.
The cross-sectional slice view of the analogous initial displacement propagating on a membrane is noticeably different from the behavior of the string, as shown at left. The initial pulse splits up into two separate pieces, one traveling to the right and the other to the left, and both travel at the same speed. However, the amplitudes of two wave pulses are not constant as they are for the string. Instead, the pulse amplitudes decay as they travel and each pulse leaves a trailing edge (or wake) behind it. The center of the membrane overshoots the zero equilibrium position.
This view shows the full two-dimensional nature of the initial displacement pulse spreading outward from the center of the membrane. The wavefront expands as an ever-increasing circle, and it is easy to see that the amplitude must decrease as the circular wavefront expands in order to conserve energy. Perhaps not as easy to believe is the fact that this circular wavefront is the result of adding up all of the contributions from rectangular mode shapes. The mathematical details may be found in the references cited at the bottom of this page.
Initial Velocity (struck at the center)
Now let's let the string and membrane be initially at rest with no initial displacement. Instead, we will strike the string or membrane, giving it an initial velocity at the center.
1-D String

Slice of a 2-D Membrane

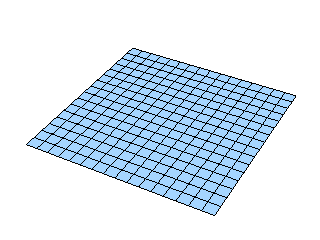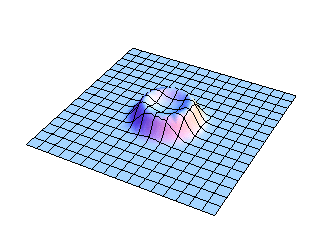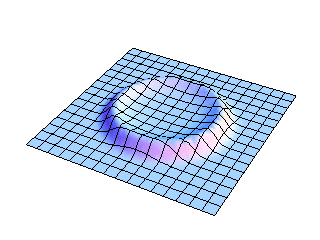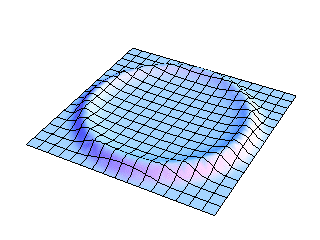
2-D Membrane
After the string is has been struck, with an initial velocity impulse, the string amplitude reaches a maximum and the pulse widens as the disturbance propagates both left and right. The upward motion of the string is slowed by the inertia and elastic restoring forces, and string eventually reaches a maximum displaced amplitude. The pulse widens as it propagates right and left, and the string remains displaced from its equilibrium. If the string is infinite in length, the string will remain displaced from the original equilibrium indefinitely; it has settled to a new equilibrium position.
If the string has a finite length, then the propagating pulses will eventually reflect from the ends. For a fixed-fixed string, struck with an initial velocity at a point, the reflections from the ends of string will result in a rectangular pulse that travels back and forth between the ends.
The cross-sectional slice of the membrane displays quite a different response to an initial velocity impulse. As the pulse widens and begins propagating both right and left, the amplitude at the center does not remain displaced as it did in the case of the string. Instead, the membrane falls back toward equilibrium as the left and right going pulses separate. Again, the waves traveling on the membrane can be seen to leave a wake behind them as the propagate outward.
The full two-dimensional view of the entire membrane shows more clearly the initial impulse falling back on itself as the circular wavefronts expand outward. The amplitude decreases as the wavefront expands, as it must to conserve energy. The wavefront shape changes as it propagates, leaving the wake behind it.
Rerences
The mathematics required to create and explain the animations on this page may be found in the following two excellent textbooks:
- Philip M. Morse, Vibration and Sound, 2nd Ed., (Acoust. Soc. Am., 1981), pp. 184-187.
- Karl F. Graff, Wave Motion in Elastic Solids, (Dover Publ., 1975), pp 217-220.
