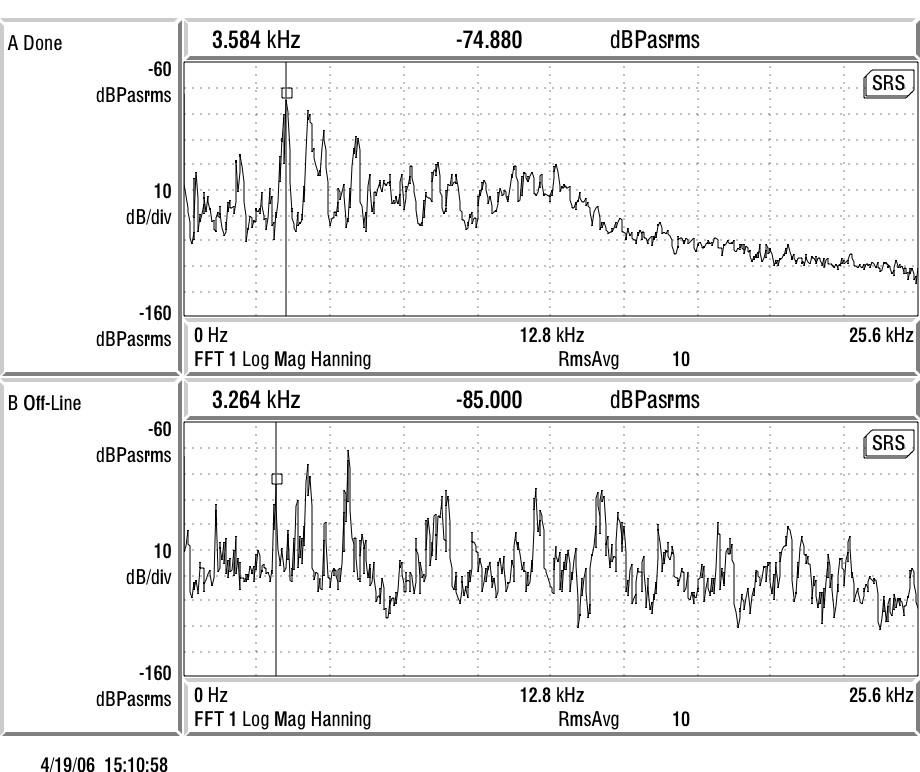
The Results
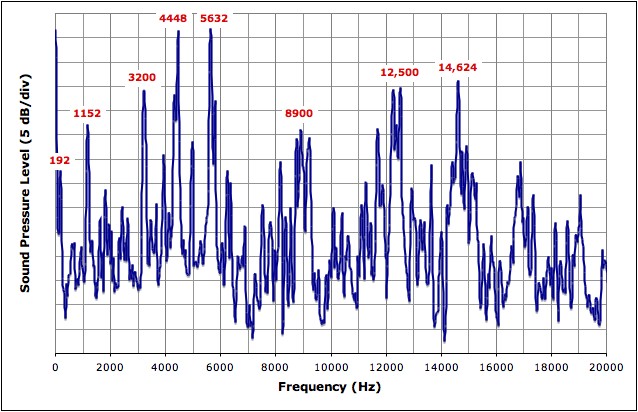
In order to catalog the important mode shapes, I am using the modal designation which is most commonly used to describe the vibration of systems with cylindrical symmetry (cylinders, bells, drums, baseball bats). Each mode shape is designated by a pair of integers, (n,m) where n represents the number of nodal diameters and m represents the number of nodal circles. A node a location (a line on a 2-D surface, or a plane in a 3-D volume) where there is no vibration for a particular mode shape. A nodal diameter indicates that there are two lines down the length of the bottle (on opposite sides of the bottle) which do not move while the rest of the bottle is vibrating. So, for a mode shape with n=2 if you traced a path around the circumference of the bottle you would encounter 4=2n lines (2 diameters = 2 pairs of lines on opposite sites of the bottle) where no vibration occurs. On one side of a nodal line the bottle will be vibrating outwards, while on the other side of the nodal line the bottle is vibrating inwards. The m integers representing nodal circles are evidenced by a line around the circumference - (a circle) at a fixed location along the length of the bottle - that does not move while the bottle is vibrating. Actually, the integer m counts the number of anti-nodes (locations of maximum amplitude) so that the number of nodal circles is really m-1. Looking at the measured mode shapes below might help. The mode shapes identified in red correspond to the most prominent peaks in the frequency spectrum above.
|
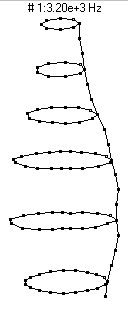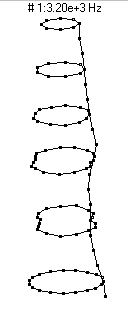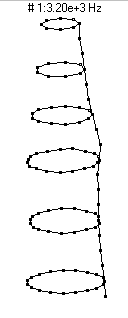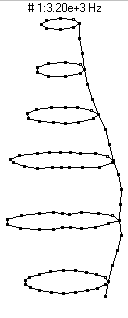 (n=2,m=1) - 3200 Hz
(n=2,m=1) - 3200 HzThe first prominent vibrational mode of the bottle is essentially a breathing mode, similar to what is observed in a bell, wineglass, or baseball bat. The mode shape designation (n=2,m=1) means that there are two nodal diameters (moving around the circumference you would find 2n=4 lines with no motion) and as you moved along the length of the bottle you would find zero (m-1) nodal circles. As the bottle vibrates it looks like it has two regions which alternate between bulging outwards and compressing inwards.
| 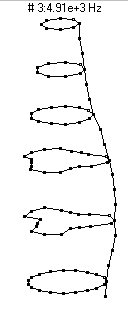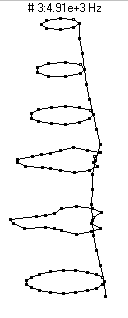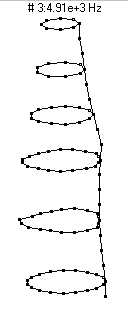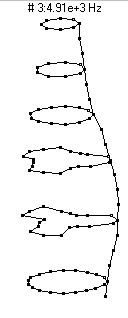 (n=3,m=1) - 4910 Hz
(n=3,m=1) - 4910 Hz
This mode, which has three nodal diameters (6 nodal lines around the circumference) and zero nodal circles, does not radiate sound nearly as well as the n=2 modes. It shows up as a peak right near 5000 Hz in the frequency spectrum at the top of the page, but has an amplitude about 25dB lower than the two most prominent peaks. As the bottle vibrates it looks like it has three regions which alternate between bulging outwards and compressing inwards.
| 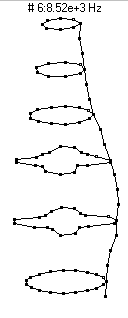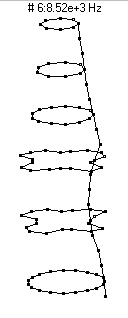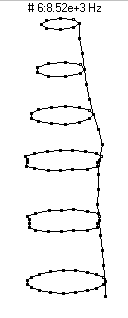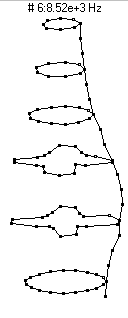 (n=4,m=1) - 8520 Hz
(n=4,m=1) - 8520 Hz
This mode has four nodal diameters (8 nodal lines around the circumference) and zero nodal circles. As the bottle vibrates it looks like it has four regions which alternate between bulging outwards and compressing inwards. This mode is a very poor radiator of sound, and thus does not show up prominently in the microphone frequency spectrum.
| 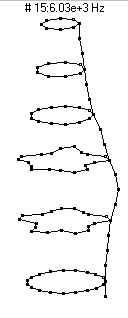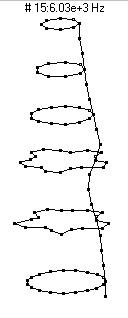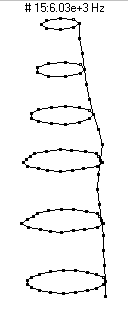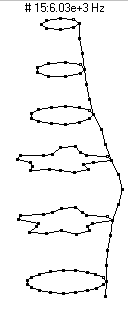 (n=5,m=1) - 13,500 Hz
(n=5,m=1) - 13,500 Hz
This mode has five nodal diameters (10 nodal lines around the circumference) and zero nodal circles. As the bottle vibrates it looks like it has five regions which alternate between bulging outwards and compressing inwards. This mode is an extremely poor radiator of sound, and does not figure prominently in the sound spectrum.
|
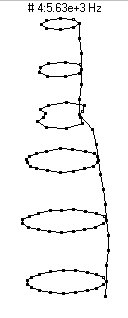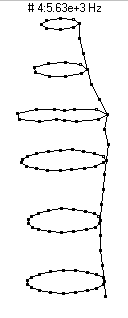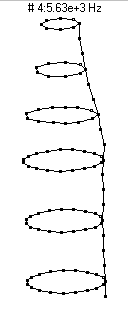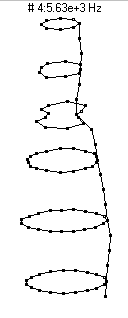 (n=2,m=2) - 5360 Hz
(n=2,m=2) - 5360 HzThe second prominent vibrational mode of the bottle is the second member of the n=2 family, with two nodal diameters and one nodal circle located about half-way up the bottle. Because this mode involves significant motion of the neck, it shows up very strongly in the sound spectrum when the bottle is struck on the neck (as would happen when clinking two bottles together to make a toast).
| 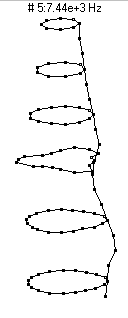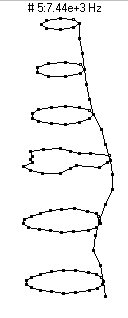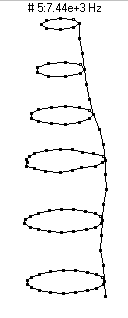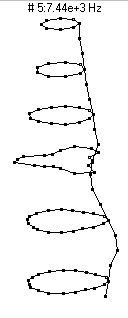 (n=3,m=2) - 7437 Hz
(n=3,m=2) - 7437 Hz
This mode shape is the second member of the n=3 family, with three nodal diameters and one nodal circle (about 3 inches or 7 dots from the bottom of the barrel).
| 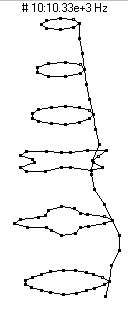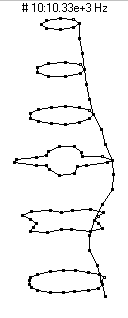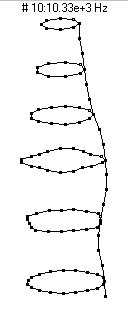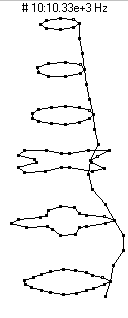 (n=4,m=2) - 10,330 Hz
(n=4,m=2) - 10,330 Hz
This mode shape is the second member of the n=4 family, with four nodal diameters and one nodal circle (about 3 inches or 7 dots from the bottom of the barrel).
| 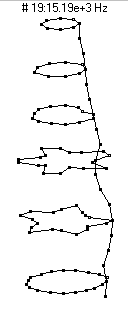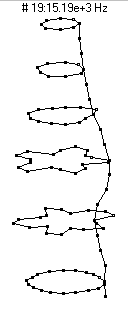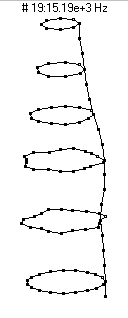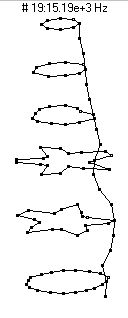 (n=5,m=2)
(n=5,m=2)
This mode shape is the second member of the n=5 family, with five nodal diameters and one nodal circle (about 3 inches or between the 7th and 8th dot from the bottom of the barrel).
|
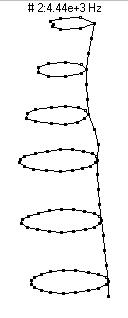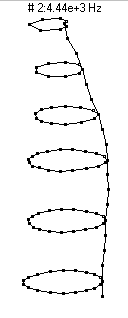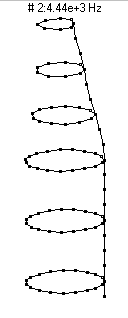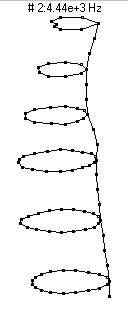 1st Bending - 4440 Hz
1st Bending - 4440 Hz
This mode is essentially a flexural bending vibration in which the entire bottle behaves like a free-free beam. Because this mode involves significant motion of the neck, it shows up very strongly in the sound spectrum when the bottle is struck on the neck (as would happen when clinking two bottles together to make a toast).
| 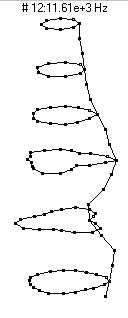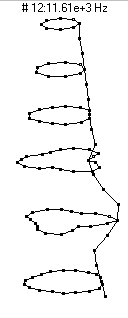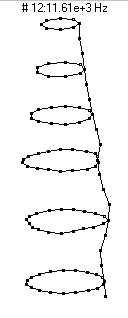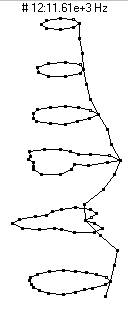 (n=3,m=3) - 11,610 Hz
(n=3,m=3) - 11,610 Hz
This mode is the third member of the n=3 family and has three nodal diameters and two nodal circles, one about 2-inches (5 dots) from the bottom and the other about 4-inches (8 dots) from the bottom.
| | |





 (n=2,m=1) - 3200 Hz
(n=2,m=1) - 3200 Hz (n=3,m=1) - 4910 Hz
(n=3,m=1) - 4910 Hz (n=4,m=1) - 8520 Hz
(n=4,m=1) - 8520 Hz (n=5,m=1) - 13,500 Hz
(n=5,m=1) - 13,500 Hz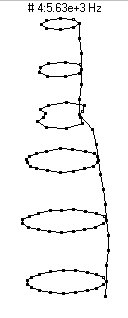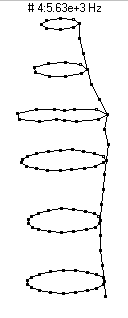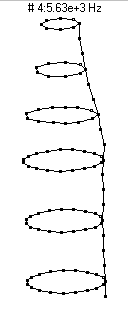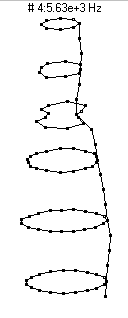 (n=2,m=2) - 5360 Hz
(n=2,m=2) - 5360 Hz (n=3,m=2) - 7437 Hz
(n=3,m=2) - 7437 Hz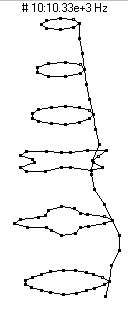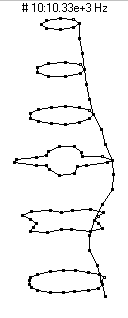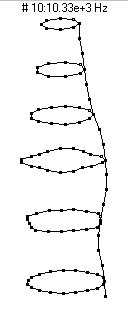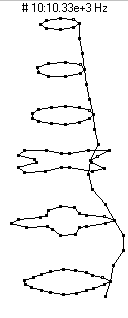 (n=4,m=2) - 10,330 Hz
(n=4,m=2) - 10,330 Hz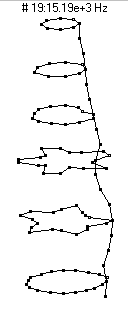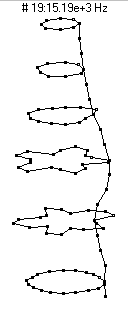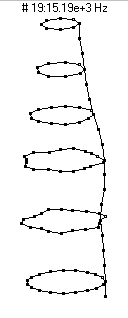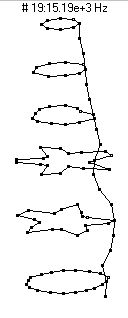 (n=5,m=2)
(n=5,m=2) 1st Bending - 4440 Hz
1st Bending - 4440 Hz (n=3,m=3) - 11,610 Hz
(n=3,m=3) - 11,610 Hz